Find the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

The rod will perform small angular oscillations about O. Let be the angular displacement,
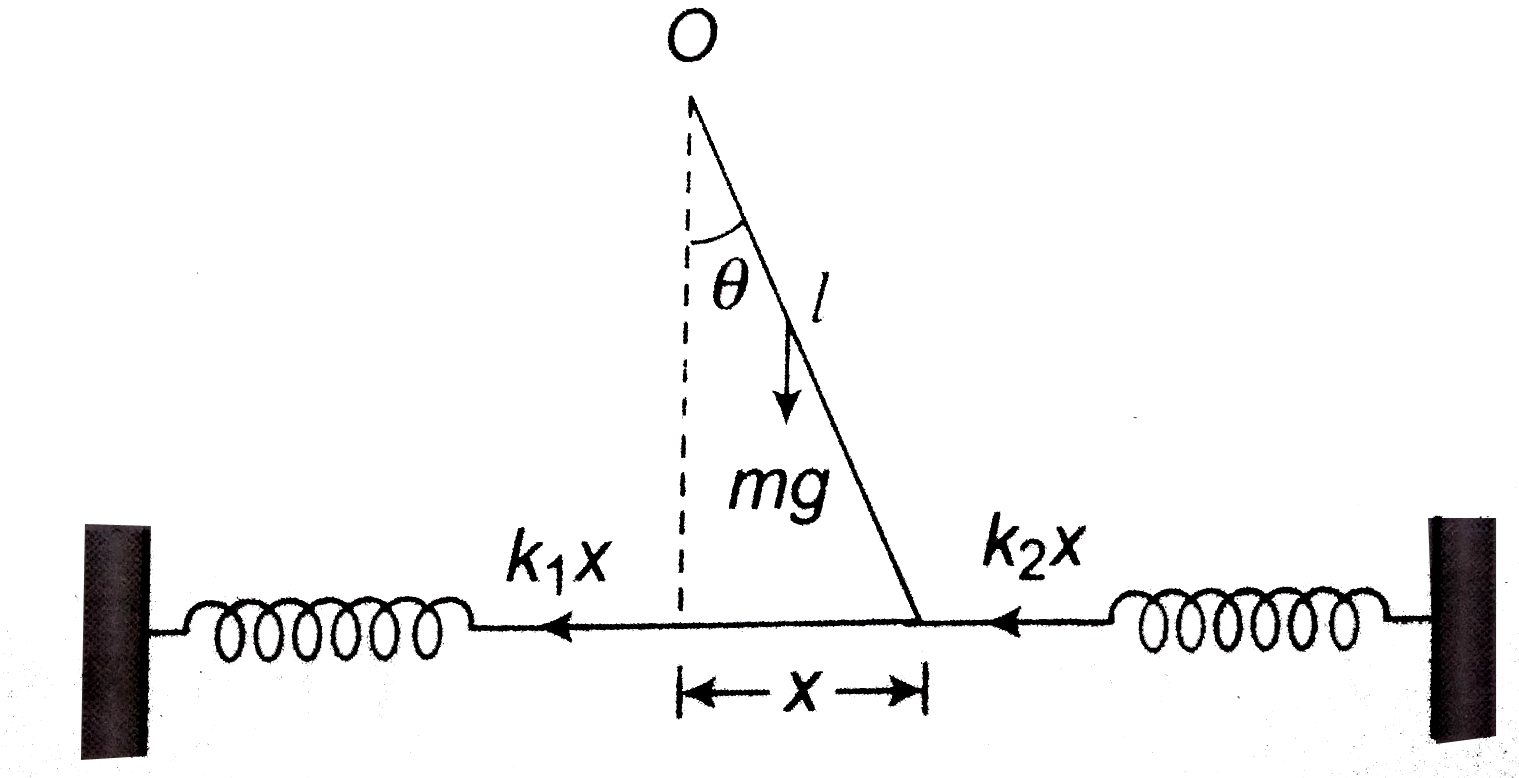
Restoring torque
Topper's Solved these Questions
Similar Questions
Find the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
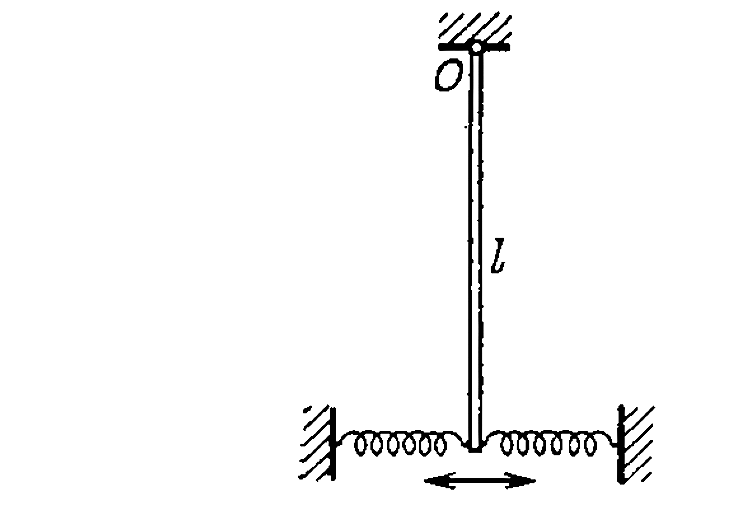
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
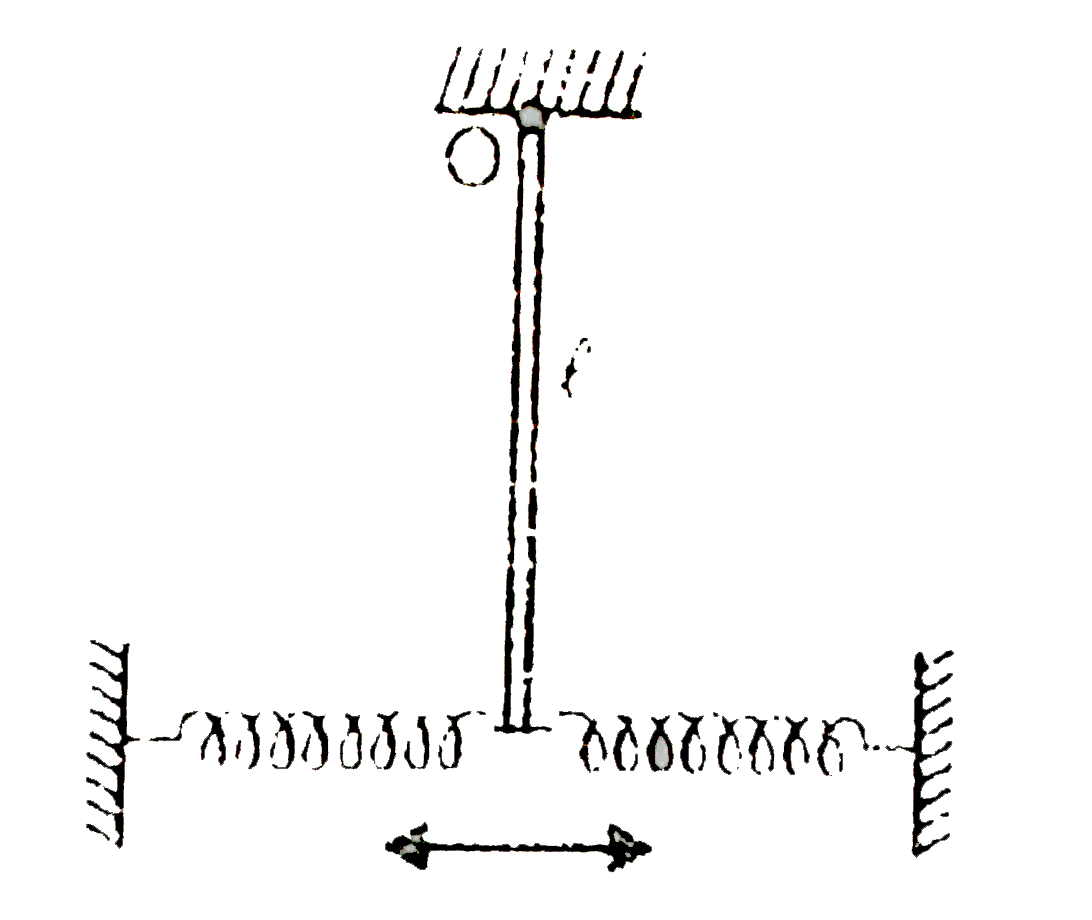
View Solution
Knowledge Check
Moment of inertia of a thin rod of mass 'M' and length 'L' perpendicular to rod at mid point is
AMl22,BMl23CMl212DNone of these
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
If the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
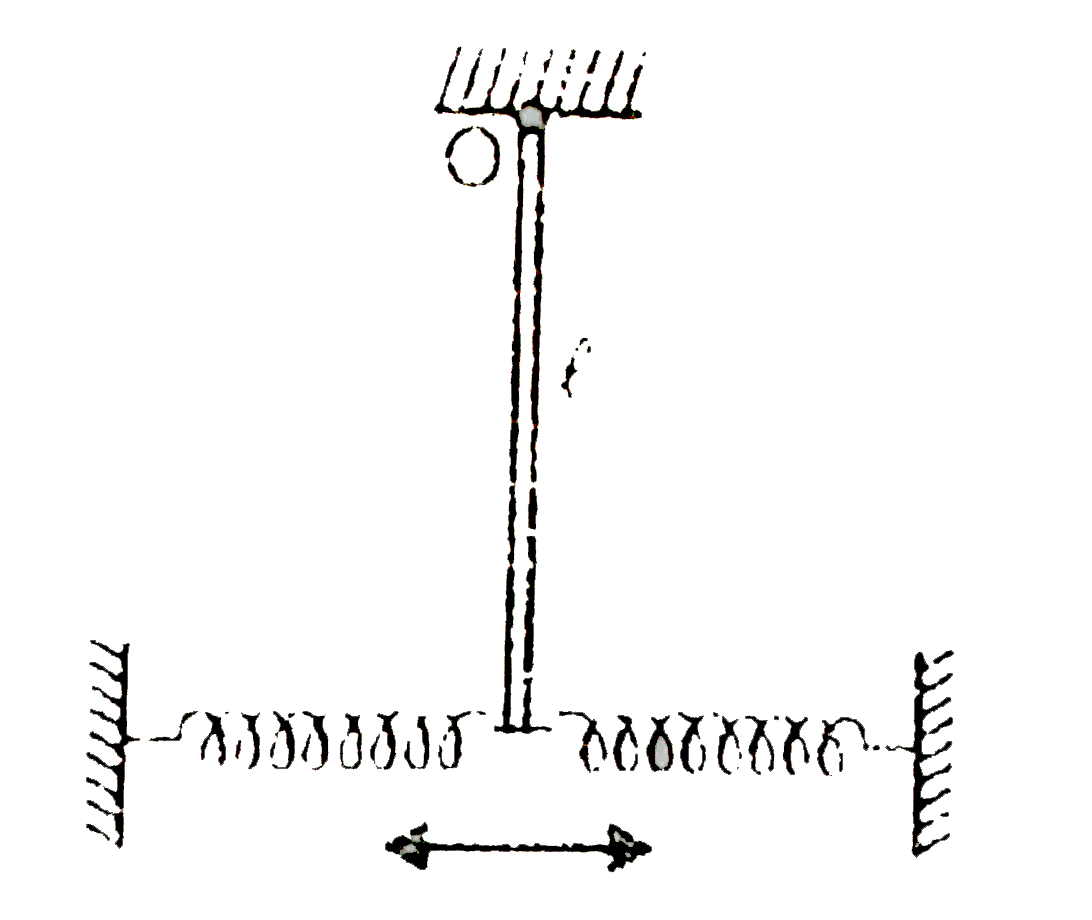
View SolutionFind the M.I. of thin uniform rod of mass M and length L about the axis as shown.
View SolutionFind the period of small oscillations of a uniform rod with length l , pivoted at one end.
View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
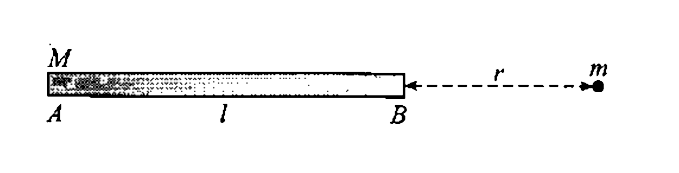
View SolutionFind the gravitational potential energy of system consisting of uniform rod AB of mass M, length l and a point mass m as shown in figure.

View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
View Solution
