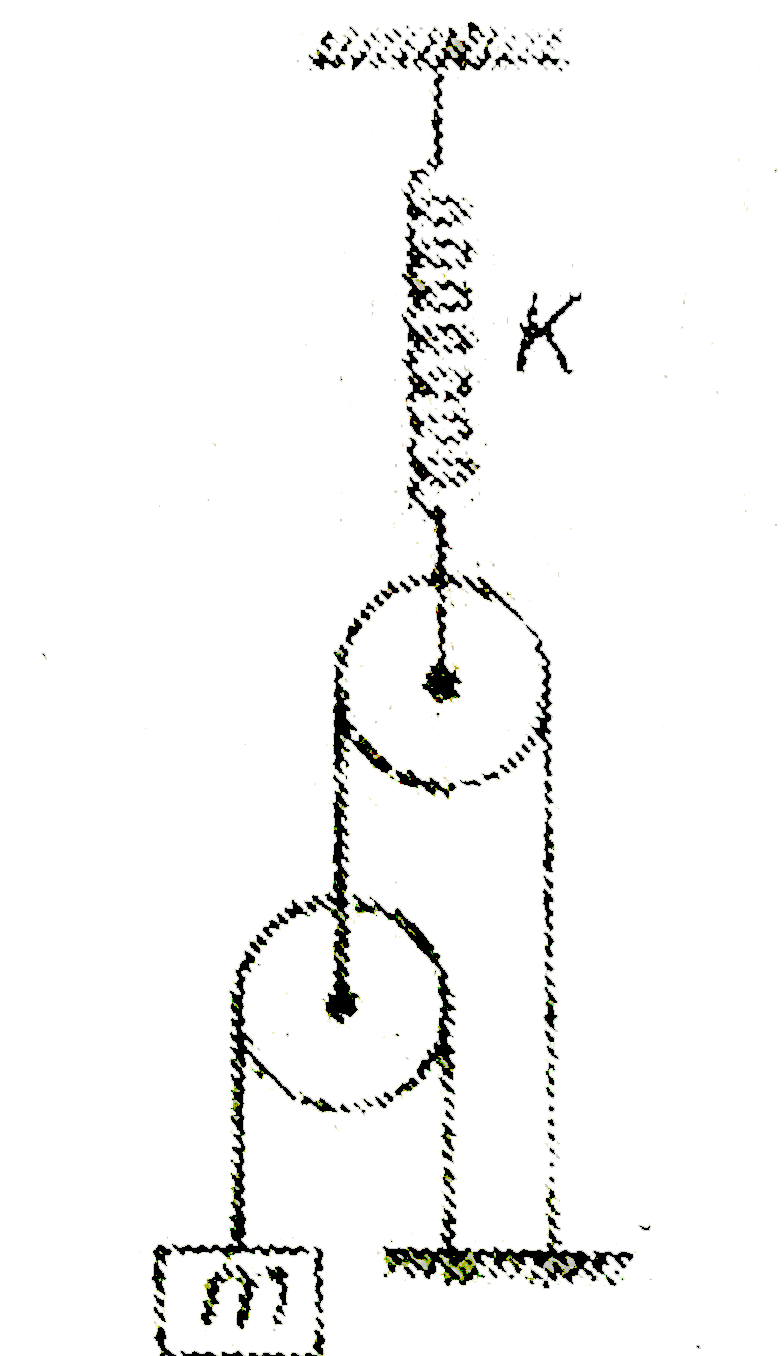
A light inextensible string carrying a springs is passed over two smooth fixed pulles as shown. If the rod is slightly displaced about the hinge form is equilibrium position, then time period is.
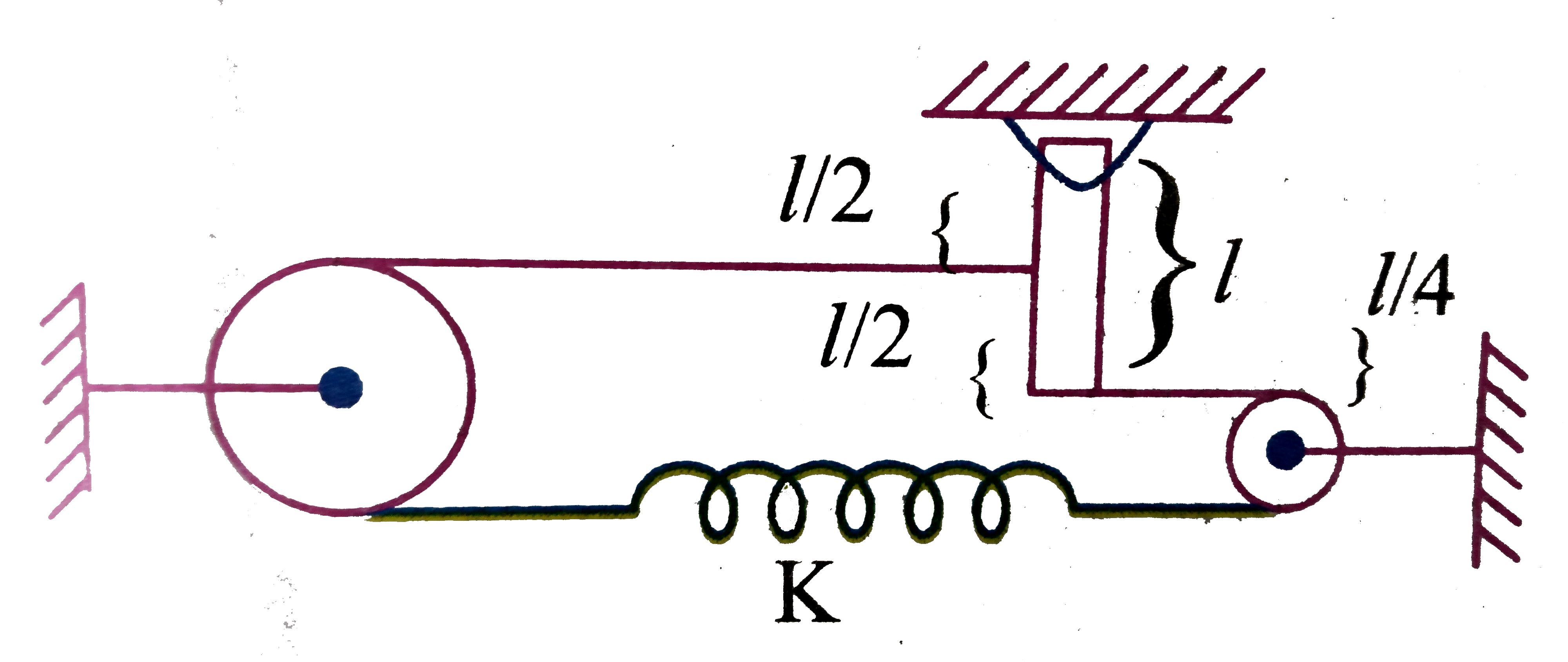
π√4ml3(kl+2mg)+π√2l3g
π√2mlkl+2mg+π√2l3
π√3mlkl2mg+π√l3
π√4mlml+2mg+π√l3
The correct Answer is:A
Let the rod is displaced by θ towards left:
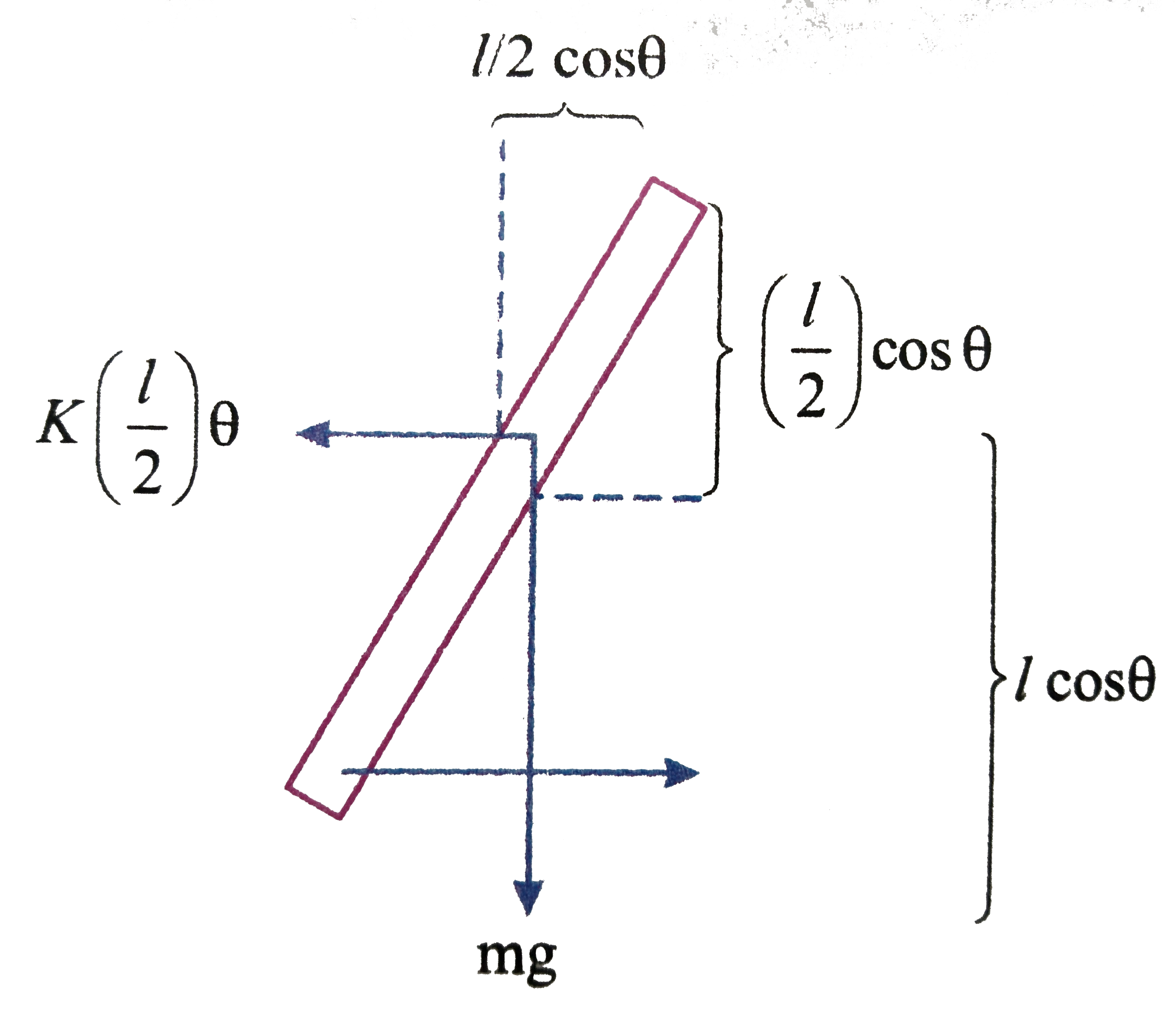
∴ net torque on rod is
−k(l2)sinθ.l2cosθ+mgsinθl2+kl2sinθlcosθ
as θ is small. sinθ→θ,cosθ→1
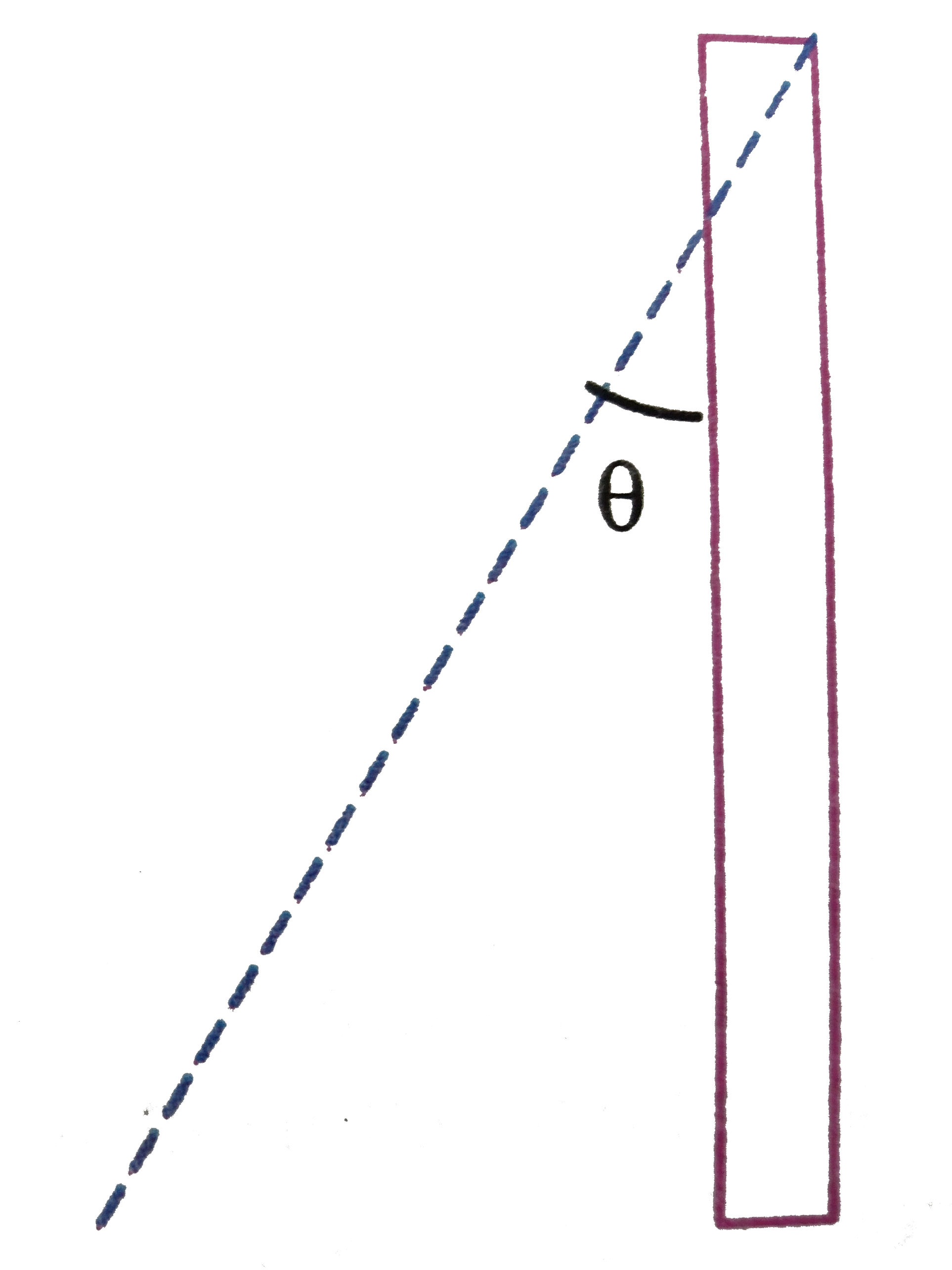
⇒τ=kl22θ+mgl2.θ−kl24θ
=[kl24+mgl2]θ=(ml23)α
∴t1=T2=π√4ml3(kl+2mg)..........(1)
When the rod is displaced right by an angle θ then string becomes slack i.e., rod becomes physical pendulum. ∴t22=T=12=2π√Imgd

where I=ml23,d=l/2, time period =t1+t2=?
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-I
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage
Explore 33 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
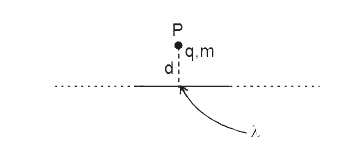
Consider the system shown below. If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of SHM.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
View Solution
Knowledge Check
Consider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
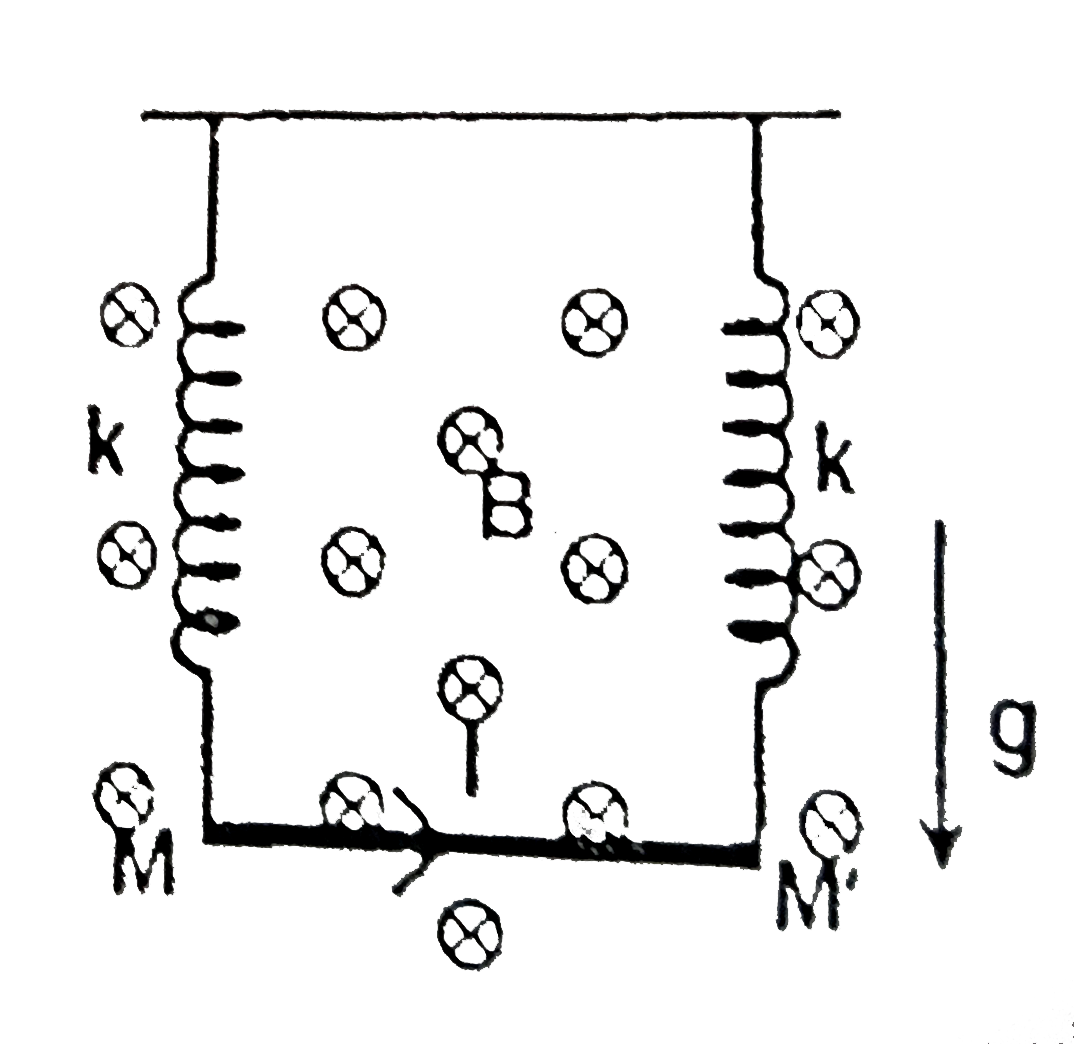 A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlBTwo masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MThe masses (M+m) and (M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
Agm/MB2gM/mCgm/2MDg(M2−m2)/2M
A block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)
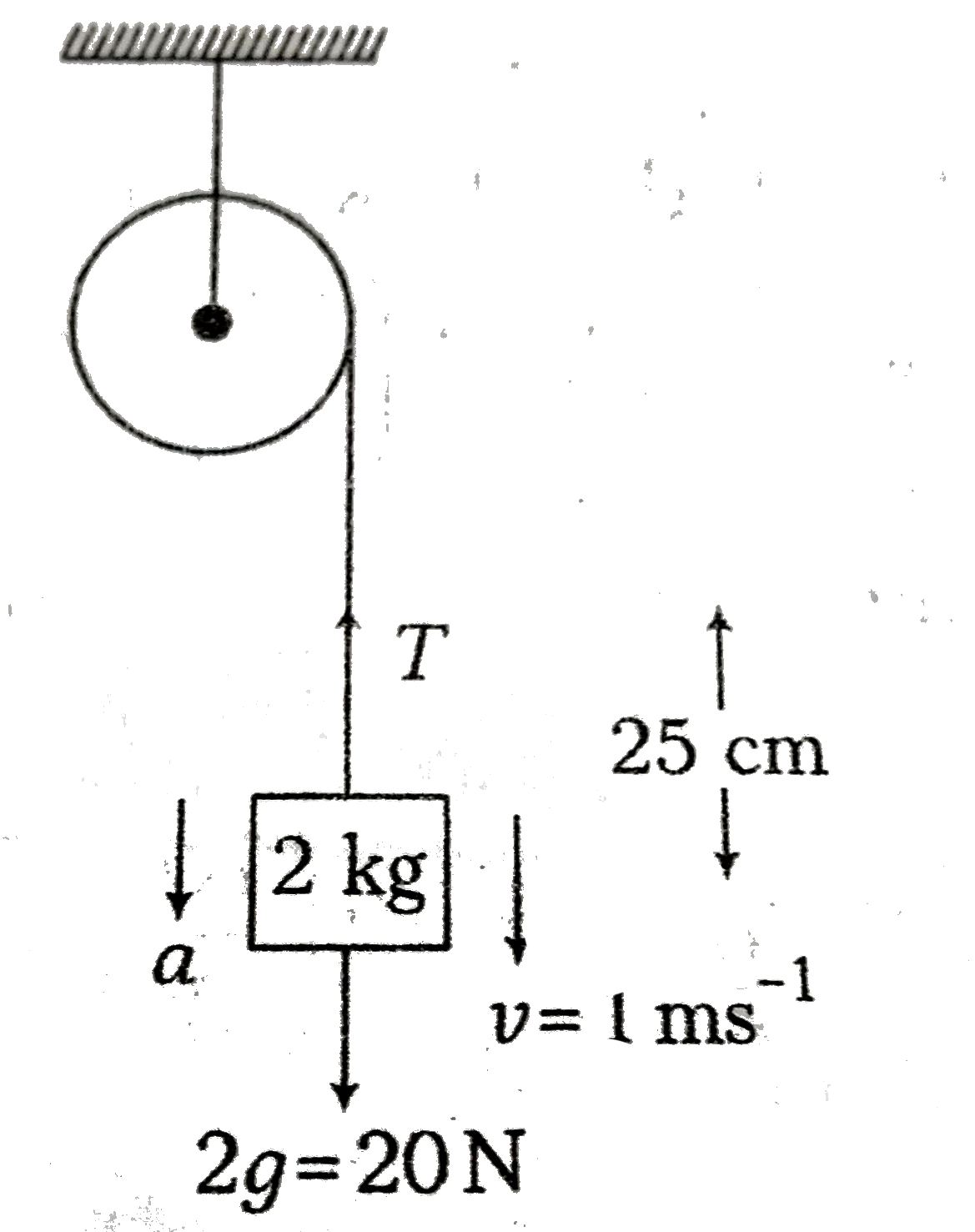
View SolutionTwo uneqal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
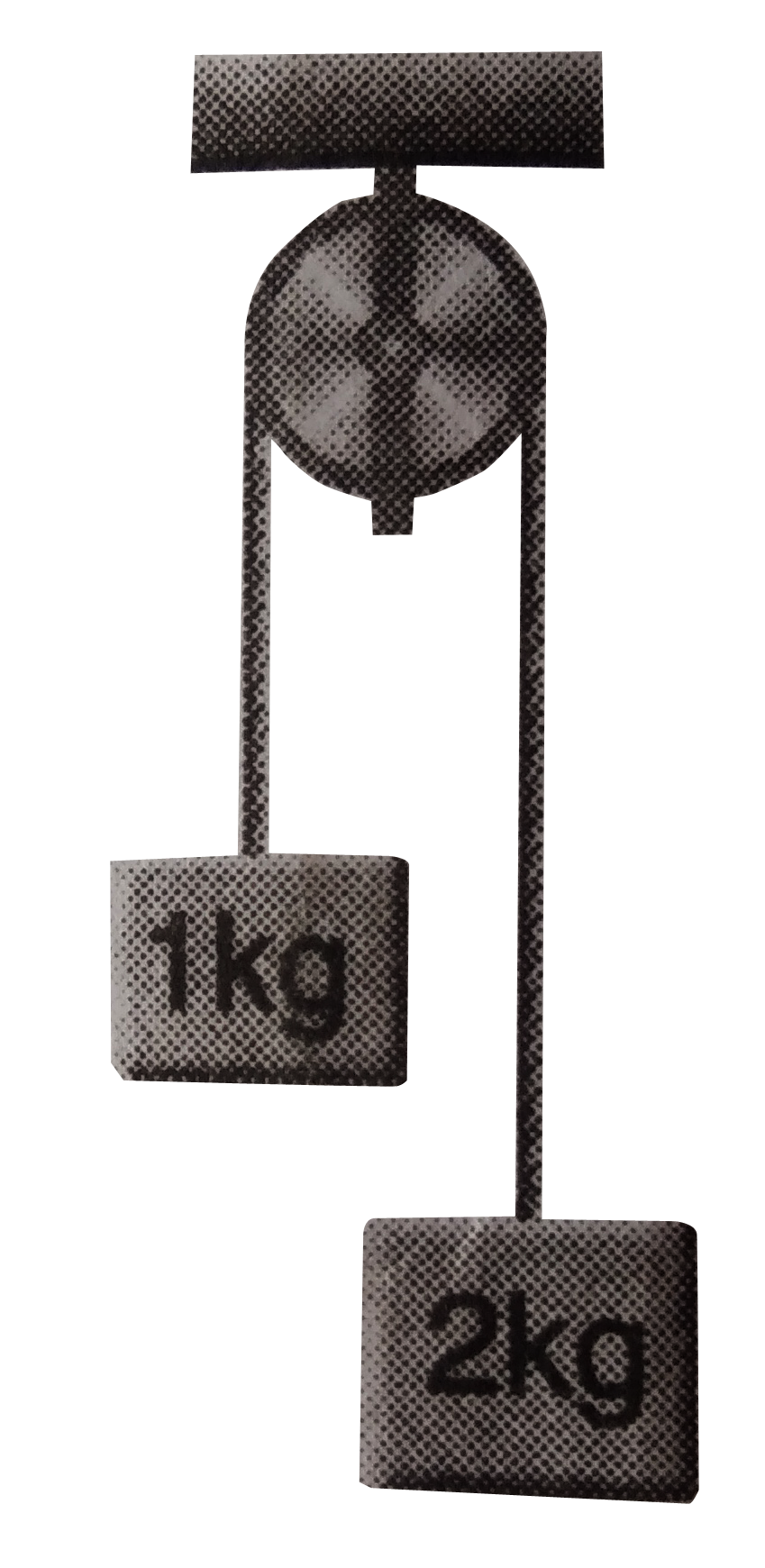
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
The displacement of block when equilibrium position is
View Solution

