The masses (M+m) and (M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
gm/M
2gM/m
gm/2M
g(M2−m2)/2M
The correct Answer is:A
To solve the problem of finding the acceleration of the system with masses (M+m) and (M−m) attached to a light inextensible string over a smooth fixed pulley, we will follow these steps:
Step 1: Identify the masses
Let:
- M1=M+m (the mass on one side of the pulley)
- M2=M−m (the mass on the other side of the pulley)
Step 2: Write the equations of motion
For mass M1 (which is M+m):
- The force acting downwards is M1g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
M1g−T=M1a(1)
For mass M2 (which is M−m):
- The force acting downwards is M2g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
T−M2g=M2a(2)
Step 3: Substitute the masses into the equations
Substituting M1 and M2 into equations (1) and (2):
1. For M1:
(M+m)g−T=(M+m)a(3)
2. For M2:
T−(M−m)g=(M−m)a(4)
Step 4: Add equations (3) and (4)
Adding equations (3) and (4) to eliminate T:
(M+m)g−T+T−(M−m)g=(M+m)a+(M−m)a
This simplifies to:
(M+m)g−(M−m)g=(M+m+M−m)a
(2m)g=(2M)a
Step 5: Solve for acceleration a
Now, we can isolate a:
a=(2m)g(2M)=mgM
Final Answer
Thus, the acceleration of the system is:
a=mgM
Let:
- M1=M+m (the mass on one side of the pulley)
- M2=M−m (the mass on the other side of the pulley)
For mass M1 (which is M+m):
- The force acting downwards is M1g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
M1g−T=M1a(1)
- The force acting downwards is M2g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
T−M2g=M2a(2)
Substituting M1 and M2 into equations (1) and (2):
1. For M1:
(M+m)g−T=(M+m)a(3)
2. For M2:
T−(M−m)g=(M−m)a(4)
Adding equations (3) and (4) to eliminate T:
(M+m)g−T+T−(M−m)g=(M+m)a+(M−m)a
This simplifies to:
(M+m)g−(M−m)g=(M+m+M−m)a
(2m)g=(2M)a
Now, we can isolate a:
a=(2m)g(2M)=mgM
Thus, the acceleration of the system is:
a=mgM
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -II (C.W)
Explore 71 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -III
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:C.U.Q
Explore 73 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
Two uneqal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
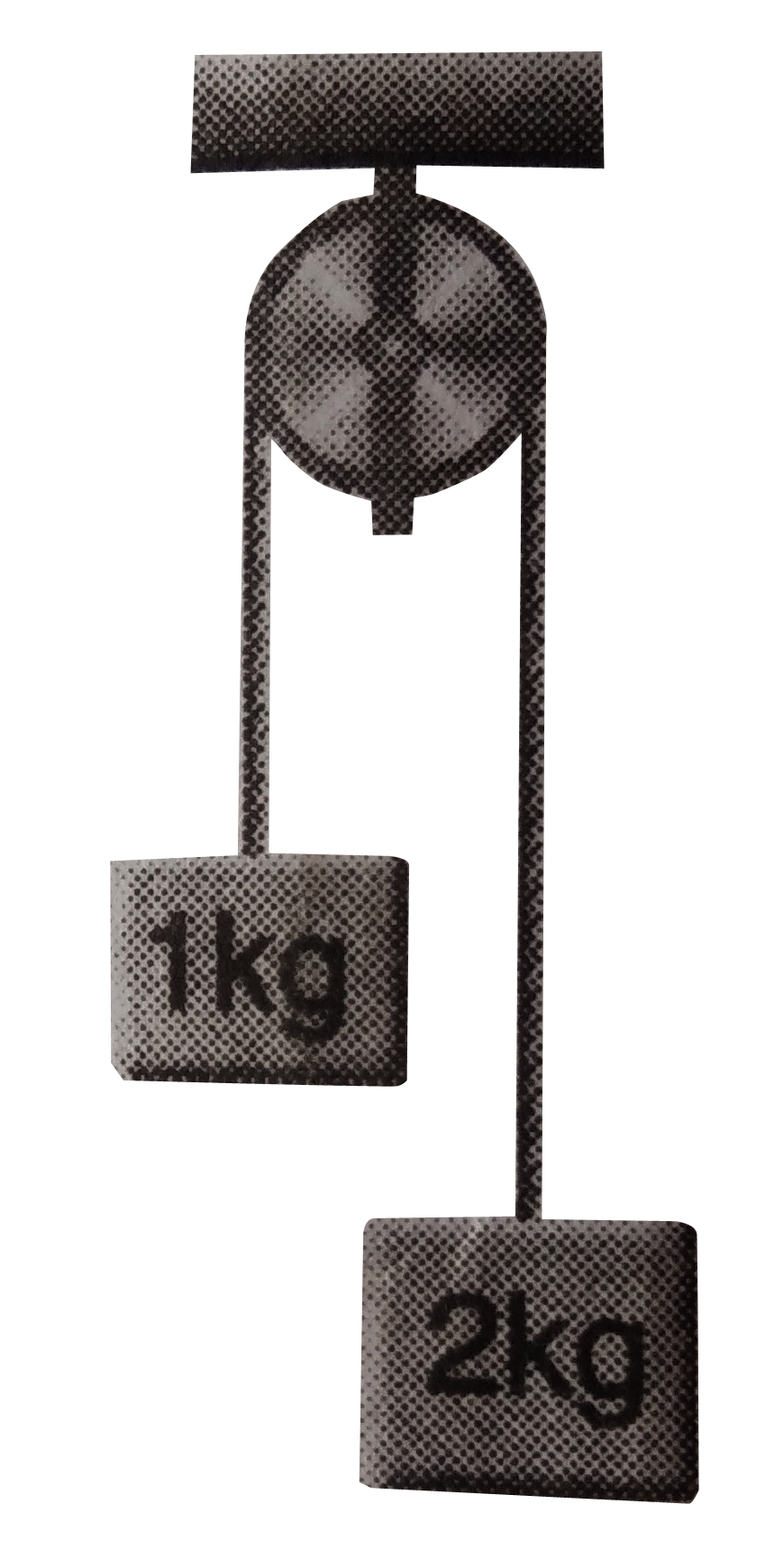
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)

View Solution
Knowledge Check
Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
 AgBg/2Cg/3Dg/4
AgBg/2Cg/3Dg/4Two particles of mass m1 and m2(m1>m2) are attached to the ends of a light inextensible string passing over a smooth fixed pulley. When the level of m1 is higher than that of m2 by 49 cm and string is just taut m2 is released. 0.5 s after motion started the masses are at the same level. the ratio of m1 to m2 is (Take g=9.8ms−2)
A7:3B4:3C3:2D2:1
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
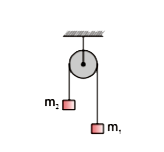
View SolutionTwo blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
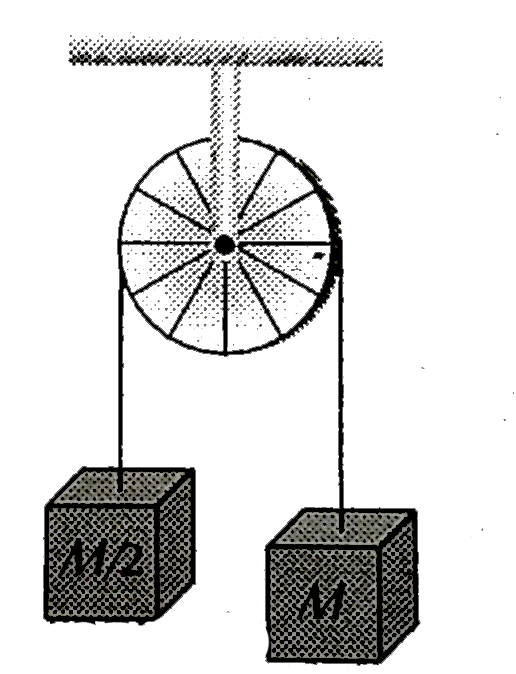
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be

View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View Solution

