Two particles move along x-axis in the same direction with uniform velocities 8m/s and 4m/s. Initially the first particle is 21 m to the left of the origin and the second one is 7 m to the right of the origin. The two particles meet from the origin at a distance of
35 m
32 m
28 m
56 m
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Define the initial positions of the particles
- Particle 1 (P1) is initially at x1=−21m (21 m to the left of the origin).
- Particle 2 (P2) is initially at x2=7m (7 m to the right of the origin).
Step 2: Define the velocities of the particles
- Velocity of Particle 1, v1=8m/s
- Velocity of Particle 2, v2=4m/s
Step 3: Set up the equations for the positions of the particles over time
Let t be the time in seconds after they start moving. The positions of the particles at time t can be expressed as:
- Position of Particle 1:
x1(t)=−21+8t
- Position of Particle 2:
x2(t)=7+4t
Step 4: Set the positions equal to find when they meet
To find the time t when the two particles meet, we set their position equations equal to each other:
−21+8t=7+4t
Step 5: Solve for t
Rearranging the equation gives:
8t−4t=7+21
4t=28
t=7s
Step 6: Find the meeting point
Now, we can substitute t=7s back into either position equation to find the distance from the origin where they meet. Using Particle 2's position:
x2(7)=7+4(7)=7+28=35m
Final Answer
The two particles meet at a distance of 35 meters from the origin.
---
- Particle 1 (P1) is initially at x1=−21m (21 m to the left of the origin).
- Particle 2 (P2) is initially at x2=7m (7 m to the right of the origin).
- Velocity of Particle 1, v1=8m/s
- Velocity of Particle 2, v2=4m/s
Let t be the time in seconds after they start moving. The positions of the particles at time t can be expressed as:
- Position of Particle 1:
x1(t)=−21+8t
- Position of Particle 2:
x2(t)=7+4t
To find the time t when the two particles meet, we set their position equations equal to each other:
−21+8t=7+4t
Rearranging the equation gives:
8t−4t=7+21
4t=28
t=7s
Now, we can substitute t=7s back into either position equation to find the distance from the origin where they meet. Using Particle 2's position:
x2(7)=7+4(7)=7+28=35m
The two particles meet at a distance of 35 meters from the origin.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 1 H.W
Explore 23 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
Similar Questions
Two particles move along the x-axis uniformly with speeds v1=8m/s and v2=4m/s. At the initial moment the first point was 21 m to the left of the origin and the second 7m to the right of the origin. When will the first point catch up with the second? Where will this take place? Plot the graph of the motion.
View SolutionA particle moves along x-axis with acceleration a=6(t−1) where t is in second. If the particle is initially at the origin and it moves along positive x-axis with v0=2m/s, find the nature of motion of the particle.
View Solution
Knowledge Check
Velocity v of a particle moving along x axis as a function of time is given by v=2tm/s. Initially the particle is to the right of the origin and 2m away from it. Find the position (distance from origin) of the particle after first 3s.
 A5 mB7 mC11 mD9 m
A5 mB7 mC11 mD9 ma particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
AThe velocityt at B is 12m/sBThe average velocity between A and B is 10m/sCThe ratio of the time to go from A to B to that from B to C is 3:2DThe average velocity between B and C is 15m/sTwo particle moving in the same direction with speeds 4m/s and 2m/s collide elastically (the collision being head on). After collision , the velocity of first particle becomes 3m/s in the same direction . The velocity of the second should be
A2m/s in same directionB4m/s in same directionC4m/s in opposite directionD5m/s in same direction
A particle is moving along a straight line with uniform retardation of 2ms−2 The initial speed of particle is 20m/s .The distance travelled by the particle during the last one second before it stops is
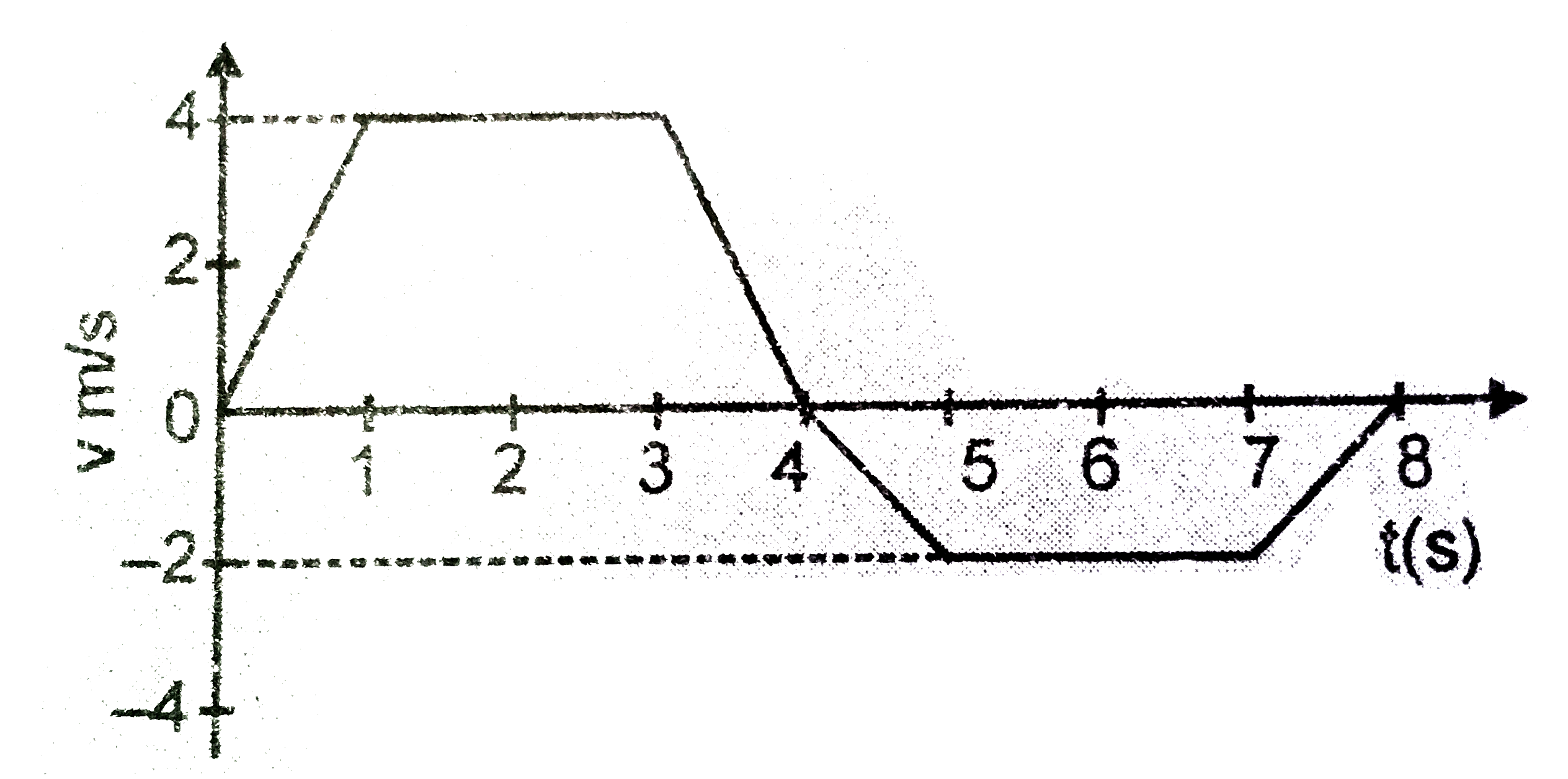
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
View SolutionTwo particles are 100m apart and start approaching each other with constant velocities of 2m/sand3m/s. The particles will meet after.
View SolutionA particle of mass 0.75 kg is moving in the XY plane parallel to Y-axis, with a uniform speed of 4 m/s. It crosses the X-axis at 3 m from the origin. What is the angular momentum of the particle about the origin?
View SolutionA particle is moving along straight line with initial velocity +7m/sec and uniform acceleration −2m/sec2 . The distance travlled by the particle in 4th second of its motion is:
View Solution

