A particle of mass 0.75 kg is moving in the XY plane parallel to Y-axis, with a uniform speed of 4 m/s. It crosses the X-axis at 3 m from the origin. What is the angular momentum of the particle about the origin?
3 kg m2/s
9 kg m2/s
6 kg m2/s
1.5 kg m2/s
The correct Answer is:B
To find the angular momentum of a particle moving in the XY plane about the origin, we can use the formula for angular momentum (L):
L=m⋅v⋅r
where:
- L is the angular momentum,
- m is the mass of the particle,
- v is the linear velocity of the particle,
- r is the perpendicular distance from the line of motion to the point about which we are calculating the angular momentum.
1. Identify the given values:
- Mass of the particle, m=0.75 kg
- Speed of the particle, v=4 m/s
- The distance from the origin to the point where the particle crosses the X-axis is r=3 m.
2. Determine the perpendicular distance:
Since the particle is moving parallel to the Y-axis and crosses the X-axis at 3 m from the origin, the perpendicular distance r from the origin to the line of motion is simply the x-coordinate of the crossing point, which is 3 m.
3. Calculate the angular momentum:
Using the formula for angular momentum:
L=m⋅v⋅r
Substitute the values:
L=0.75kg⋅4m/s⋅3m
4. Perform the multiplication:
L=0.75⋅4⋅3=9kg m2/s
5. Conclusion:
The angular momentum of the particle about the origin is 9kg m2/s.
- L is the angular momentum,
- m is the mass of the particle,
- v is the linear velocity of the particle,
- r is the perpendicular distance from the line of motion to the point about which we are calculating the angular momentum.
- Mass of the particle, m=0.75 kg
- Speed of the particle, v=4 m/s
- The distance from the origin to the point where the particle crosses the X-axis is r=3 m.
Since the particle is moving parallel to the Y-axis and crosses the X-axis at 3 m from the origin, the perpendicular distance r from the origin to the line of motion is simply the x-coordinate of the crossing point, which is 3 m.
Using the formula for angular momentum:
L=m⋅v⋅r
Substitute the values:
L=0.75kg⋅4m/s⋅3m
L=0.75⋅4⋅3=9kg m2/s
The angular momentum of the particle about the origin is 9kg m2/s.
Topper's Solved these Questions
Similar Questions
A particle of mass m=5kg is moving with a uniform speed v=3√2 in the XOY plane along the line Y=X+4. The magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m=5kg is moving with a uniform speed v=3√2 in the XOY plane along the line Y=X+4. The magnitude of the angular momentum of the particle about the origin is
View Solution
Knowledge Check
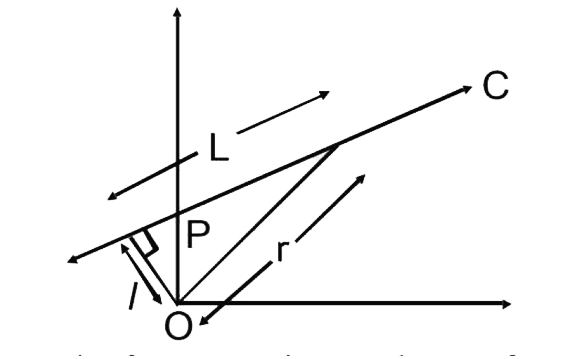
A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
 AmvLBmvICmvrDzero
AmvLBmvICmvrDzeroA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDzero
AmvLBmvlCmvrDzeroA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDZero
AmvLBmvlCmvrDZero
A particle of mass m = 5 units is moving with a uniform speed v=3√2 units in the XOY plane along the line Y = X + 4. The magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m=5 unit is moving with a uniform speed v=3√2 unit in the XOY plane along the line y=x+4 the magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m=5 unit is moving with a uniform speed v=3√2 unit in the XOY plane along the line y=x+4 the magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass 80 units is moving with a uniform speed v=4√2 units in XY plane, along a line y=x+5. The magnitude of the angular momentum of the particle about the origin is
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
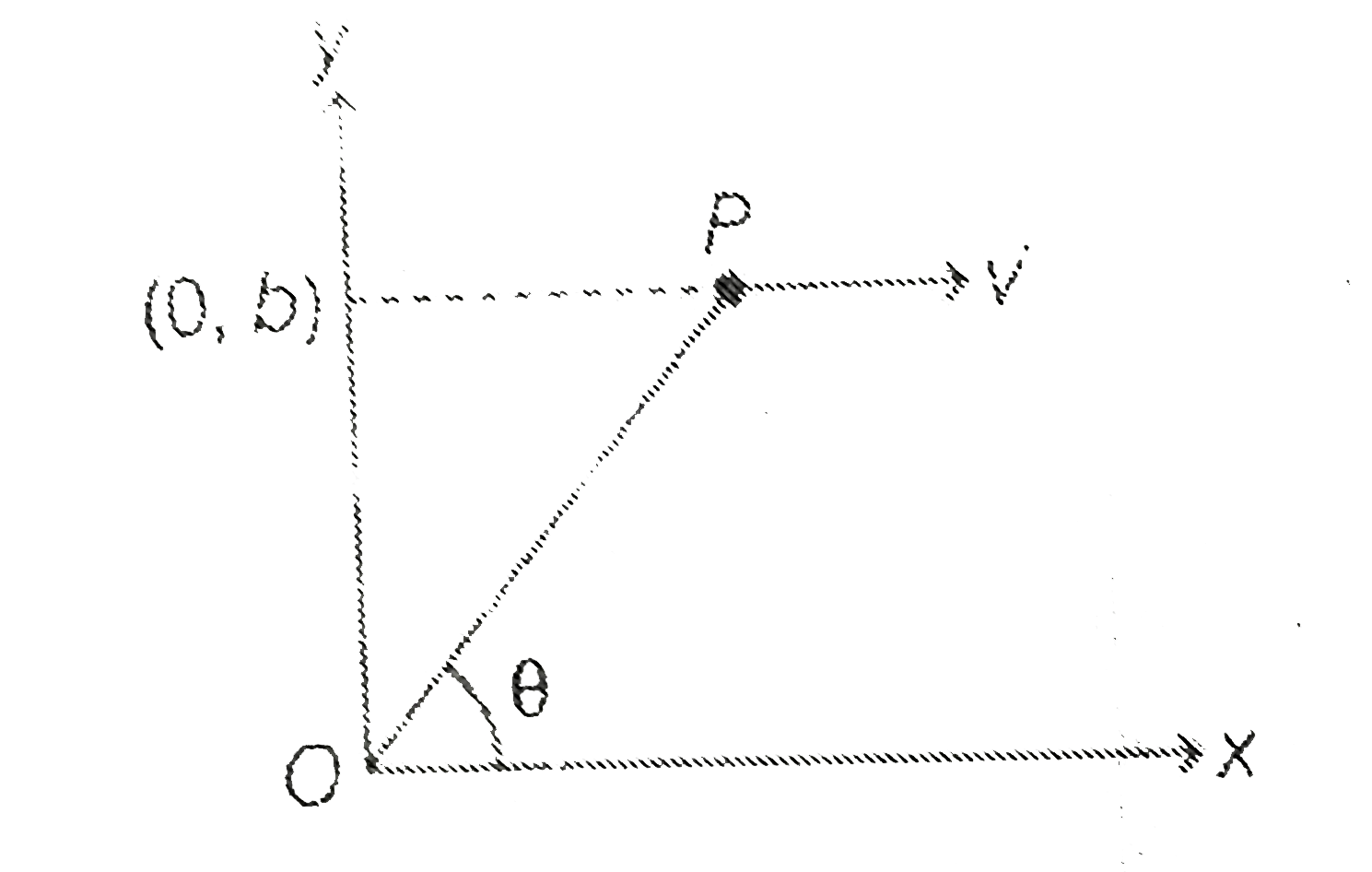
View Solution

