A heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is , the maximum percentage of the length of the chain that can hang over one edge of the table is
The correct Answer is:A
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -II (C.W)
71 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -III
31 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - C.U.Q
73 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV
41 Videos
Similar Questions
A uniform chain of length L is lying partly on a table, the remaining part hanging down from the edge of the table. If the coefficient of friction between the chain and the table is 0.5 what is the minimum length of the chain that should lie on the table, to prevent the chain from slipping down to the ground.
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
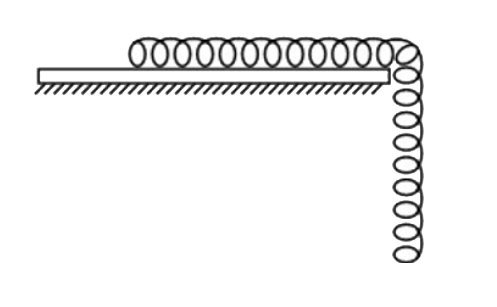
View Solution
Knowledge Check
A heavy uniform chain lies on a horizontal table-top. If the coefficient of friction between the chain and table surface is 0.25, then the maximum fraction of length of the chain, that can hang over one edge of the table is
A0.2B0.25C0.35D0.15A heavy uniform chain lies on horizontal table top. If the coeficient of friction 0.25, then the maximum friction of length of the chain that can hang over on edge of the table is
A20%B25%C35%D15%A homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
A(μμ+1)LB(1−μμ)LC(1−μ1+μ)LD(2μ2μ+1)L
If the coefficient of static friction between a table and a uniform massive rope is μ, what fraction of the rope can hang over the edge of a table without the rope sliding.
View SolutionA rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient of friction between chain and inclined plane is H, the maximum length of the hanging part to prevent the chain from falling vertically is 30°
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?

View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
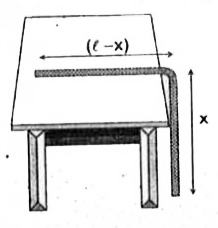
View SolutionA uniform rope of length l lies on a table. If the coefficient of friction is μ, then the maximum length L of the part of this rope which can overhang from the edge of the table without sliding down is
View Solution
