A particle pendulum is positioned such that is centre of gravity is vertically above suspension point. From that position the pendulum started moving tward the stable equilibroum and passed it with an angular velocity $ω$ . By neglecting the friction at point of suspension, the period of small oscillations of the pendulum is

A

$\frac{2 π}{ω}$

B

$\frac{4 π}{ω}$

C

$\frac{π}{ω}$

D

$\frac{5 π}{ω}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

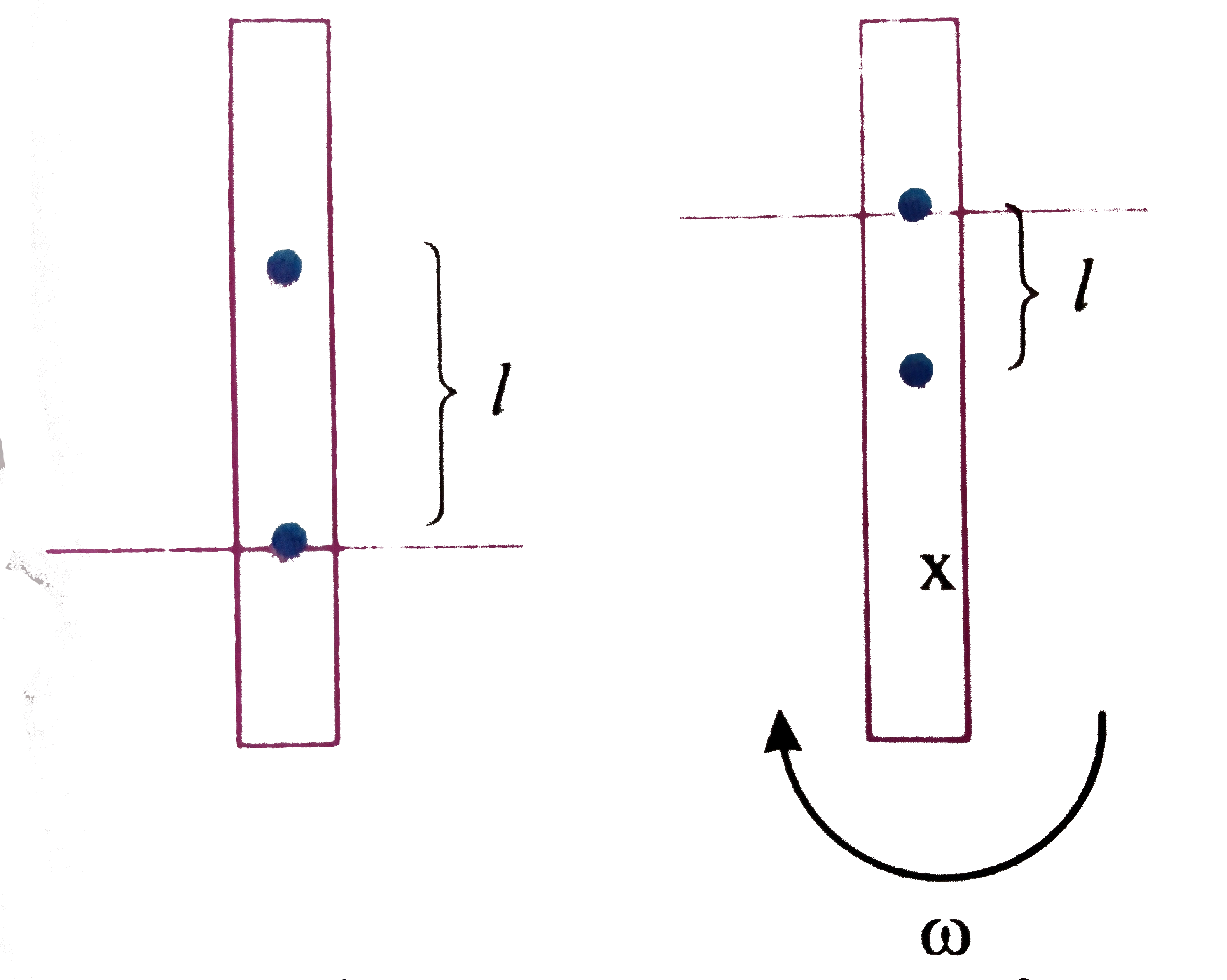
From law of conservation of energy
$m g (2 l) = \frac{1}{2} I ω^{2} \dots \dots \dots . . (1)$
Time period: $T = 2 π \sqrt{\frac{I}{m g l}} \dots \dots \dots \dots \dots . (2)$
Solve (1) & (2), to get $T = ?$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A physical pendulum is positioned so that its centre of gravity is above the suspension point. When the pendulum is realsed it passes the point of stable equilibrium with an angular velocity $ω$ . The period of small oscollations of the pendulum is
A $\frac{4 π}{ω}$
B $\frac{2 π}{ω}$
C $\frac{π}{ω}$
D $\frac{π}{2 ω}$
Question 2 - Select One or More
When the point of suspendion of pendulum is moved, its period of oscillation
Adecreaes when it moves vertically upwards with an acceleration $a$
Bdecreases when it moves vertcally downwards with acceleration greater than 2 g.
CIncreases when it moves horizontally with acceleration $a$
Dall of the above.
Question 3 - Select One
The distance between the points of suspension and centre of oscillation for a compound pendulum is :
A $\frac{k^{2} - l^{2}}{2}$
B $\frac{k^{2} + l^{2}}{l}$
C $\frac{k^{2} + l^{2}}{2 l}$
D $k + \frac{l^{2}}{k}$

NARAYNA-OSCILLATIONS-SINGLE ANSWER QUESTIONS

Home
Ask Doubt
Profile