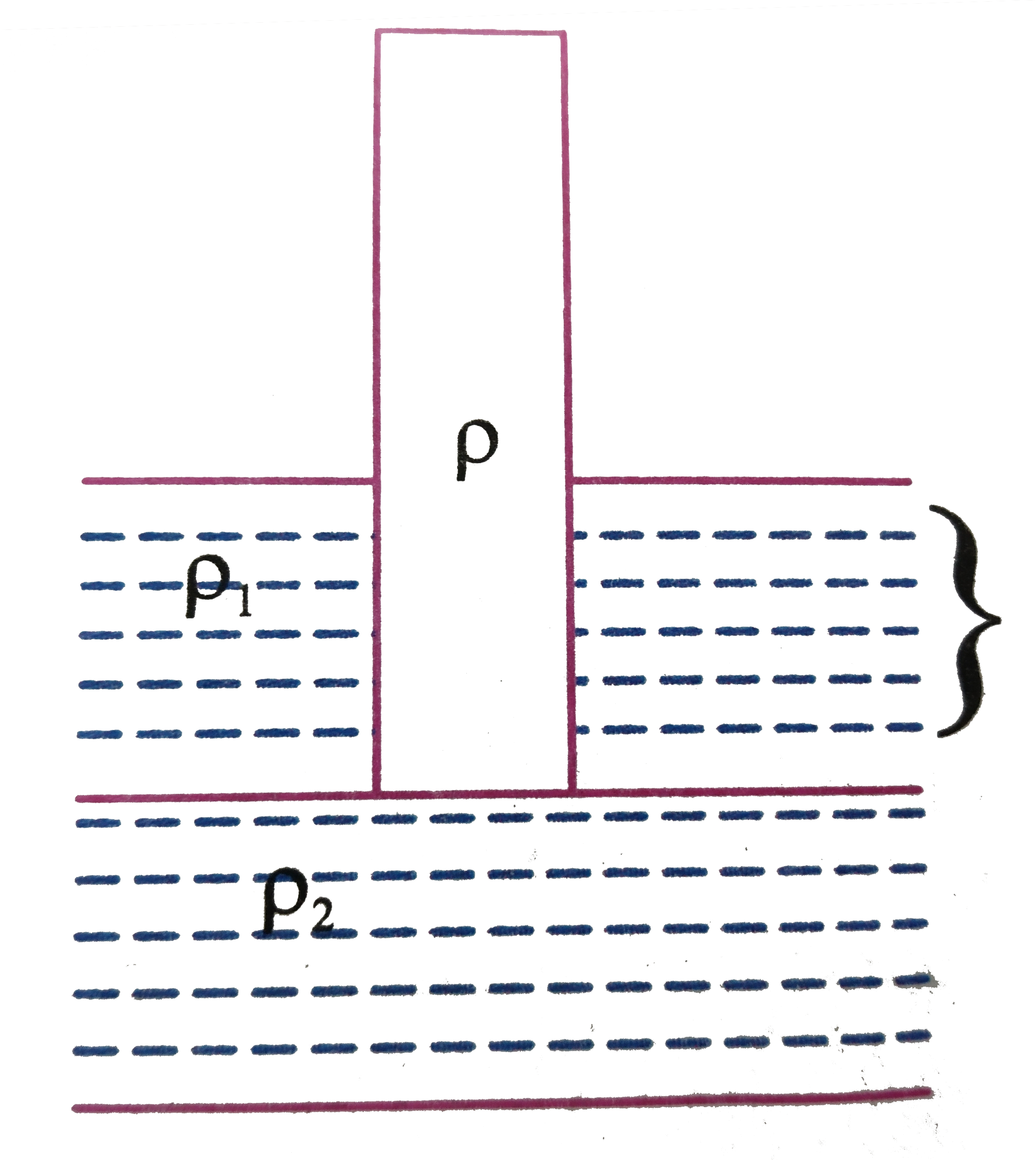
A vertical pole of length l, density ρ, area of cross section A, floats in two immiscible liquids of densities ρ1 and ρ2. In equilibrium position the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, the time period of oscillation is..........
π√ρl(ρ1+ρ2)g
π√ρlg(1√ρ1+1√ρ2)
π√(ρ1+ρ2)lρg
π√lρg(√ρ1+√ρ2)
The correct Answer is:B
Here interface acts as mean position of SHM:
∴ time period, T=T12+T22
T1=2π√ρlρ2g:T2=2π√ρlρ1g
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Video
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
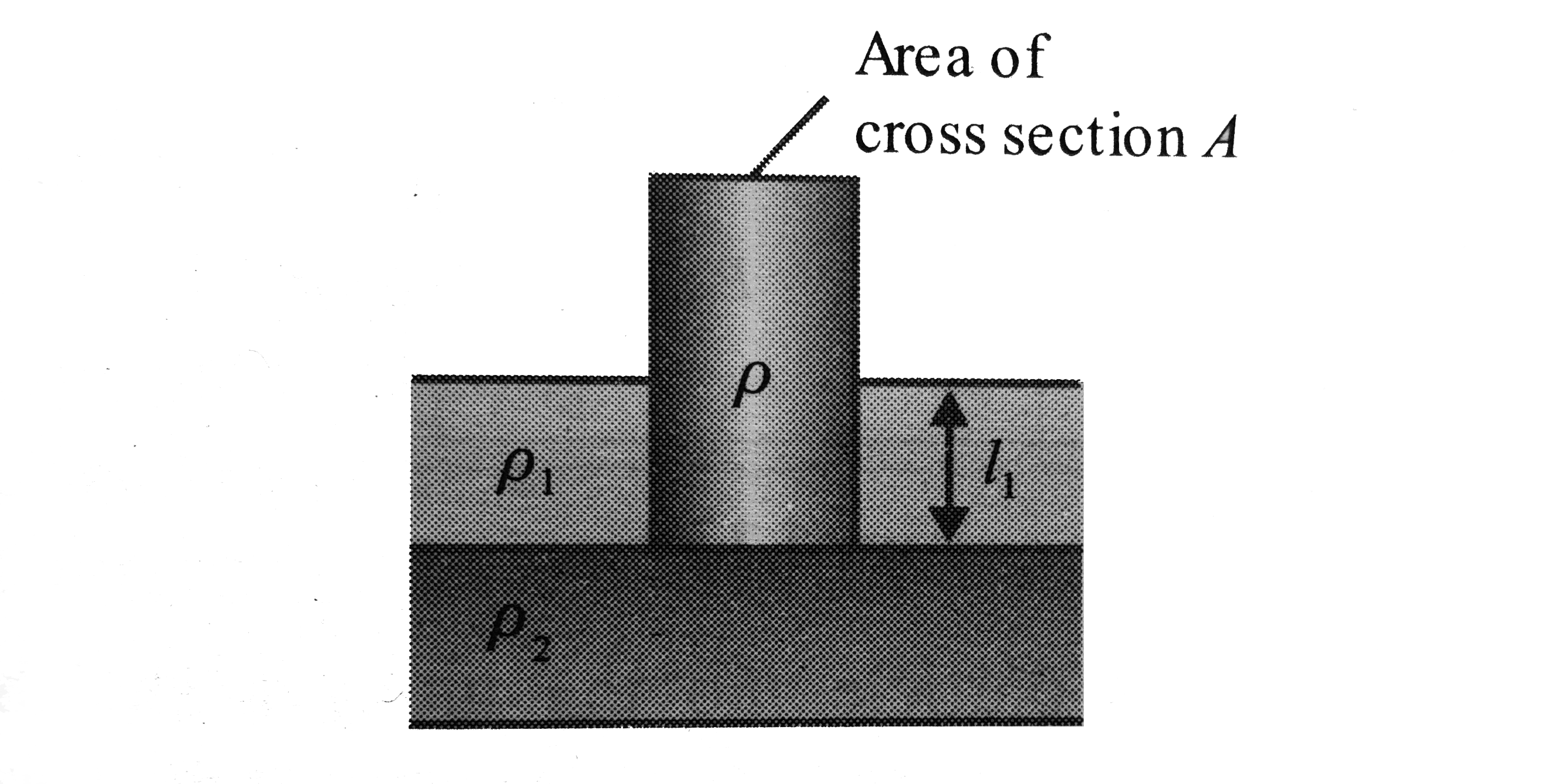
View SolutionTwo immiscible liquids of densities ρ and 2ρ and thickness (heights) h and 2h, respectively, push a vertical plate. Find the total side thrust given by the liquids on the vertical plate.

View Solution
Knowledge Check
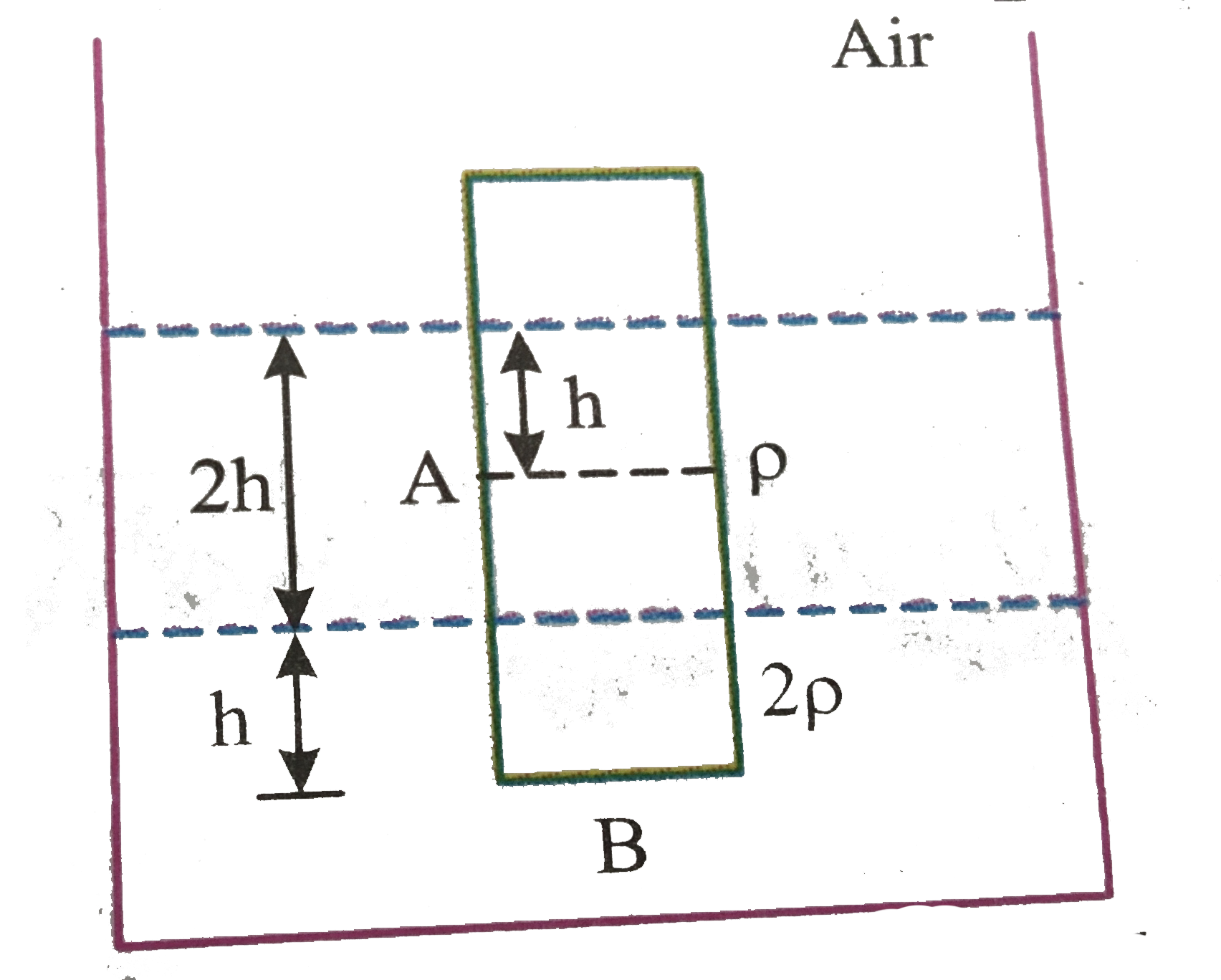
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:A2πghB3ρghC4ρghDnoneIf two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2If two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2roh1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2
If two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View SolutionA rectangular block of mass m and area of cross section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes with a time period T, then
View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View Solution