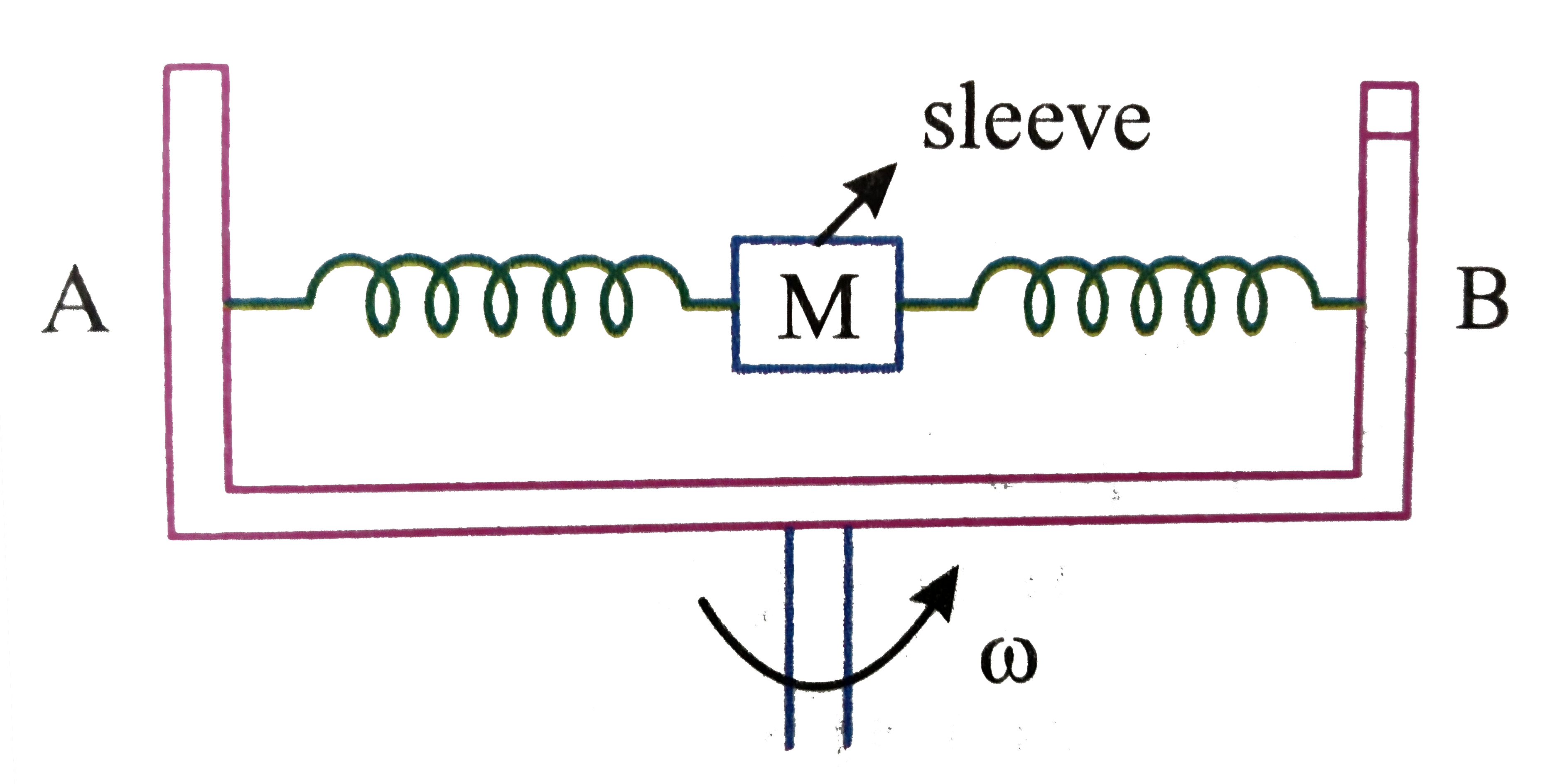
In the arrangement shown, the sleeve of mass M is fixed between two identical springs whose combined force constant is k. The sleeve can slide without friction over a horizontal bar AB. The arragement rotates with a constant angular velocity ω about a vertical axis passing through the middle of the bar. the period of small oscillations of teh sleeve is.........
2π√mk
2π√mk−mω2
π√mk
π√mk−mω2
The correct Answer is:B
Let x be the displacement of sleeve in disturbed condition along horizontal bar from centre. The free body diagram is:
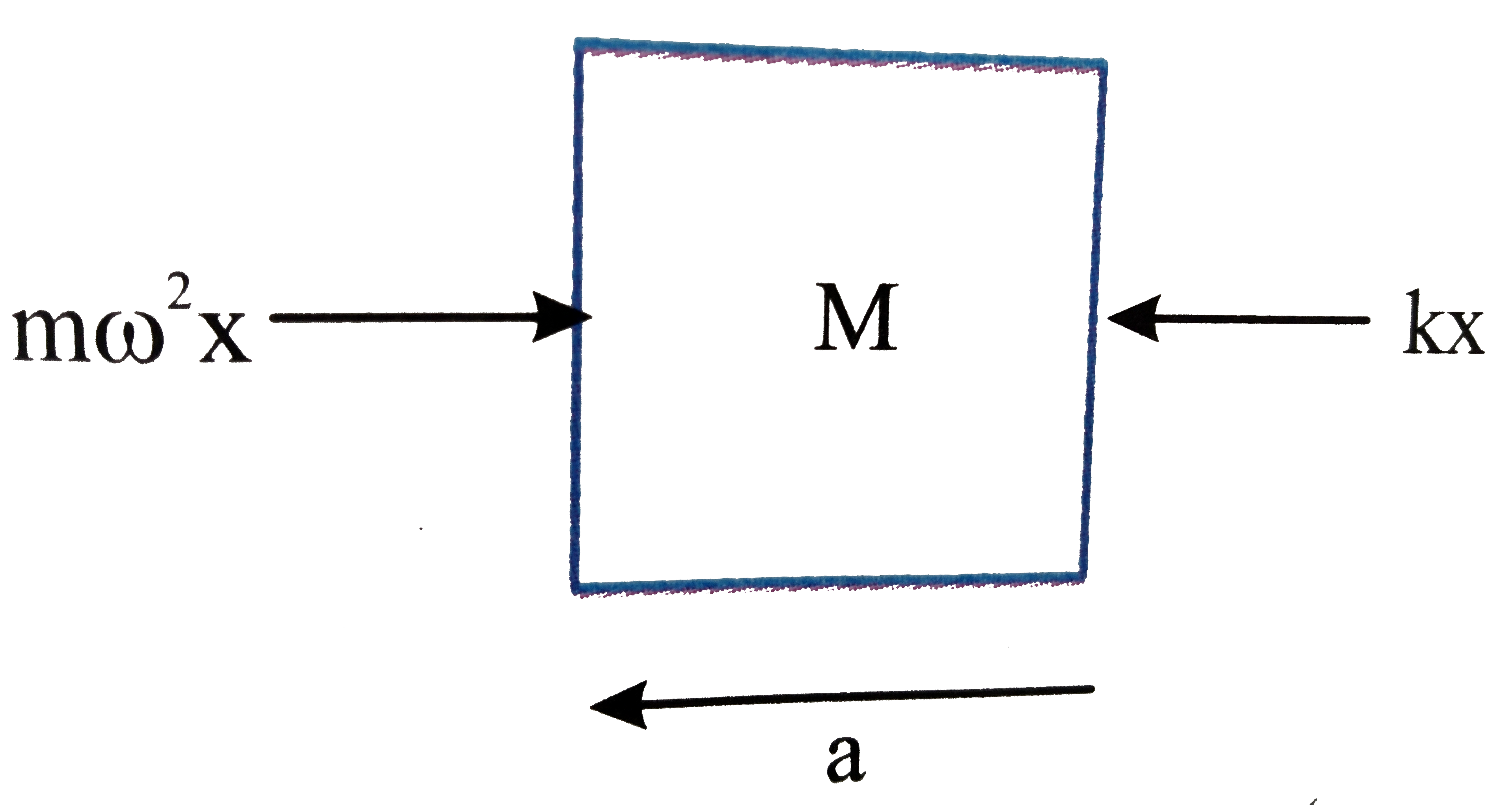
∴Frestoring=kx−mω2x⇒ma=(k−mω2)x
⇒a=(k−mω2)mxT=?
[∵ do not confuse angular velocity of frame with angular frequency of SHM]
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-I
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage
Explore 33 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
In the arrangement shown in figure the sleeve M of mass m=0.20kg is fixed between two identical springs whose combined stiffness is equal to x=20N/m. The sleeve can slide without friction over a horizontal bar AB. The arrrangement rotates with a constant angular velocity ω=4.4rad/s about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve ?
View SolutionA particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View Solution
Knowledge Check
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY
A sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R(figure). The system is set in rotation with a constant angular velocity ω about a vertical axis OO′. Find the angle θ corresponding to the steady position of the sleeve.
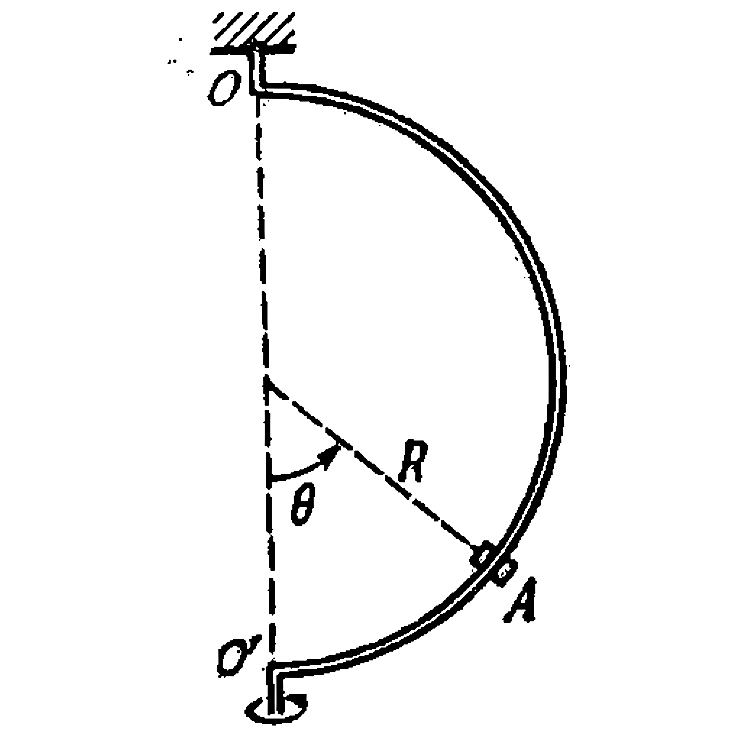
View SolutionA sleeve A can slide freely along a smooth rod bent in the shape of a half circle of radius R .The system is set in rotaion with a constant angular velocity ω about a vertical axis OO' .Find the angle θ corresponding to the steady position of the sleeve

View SolutionA device (figure) consists of a smooth L-shaped rod located in a horizontal plane and a sleeve A of mass m attached by a weight less spring to a point B. The spring stiffness is equal to x. The whole system rotates with a constant angular velocity ω about a vertical axis passing through the point O. Find the elongation of the spring. How is the result affected by the rotation direction?
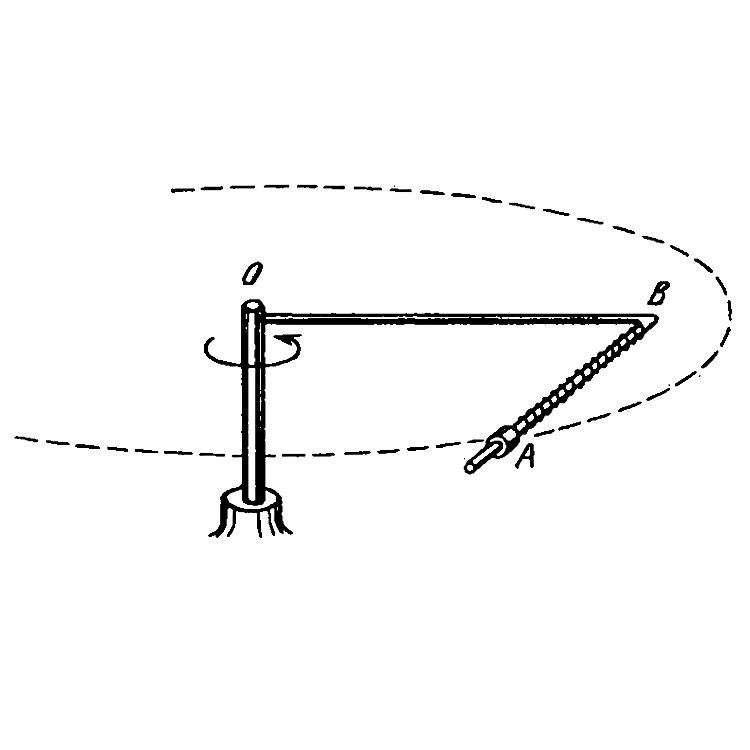
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is

View Solution

