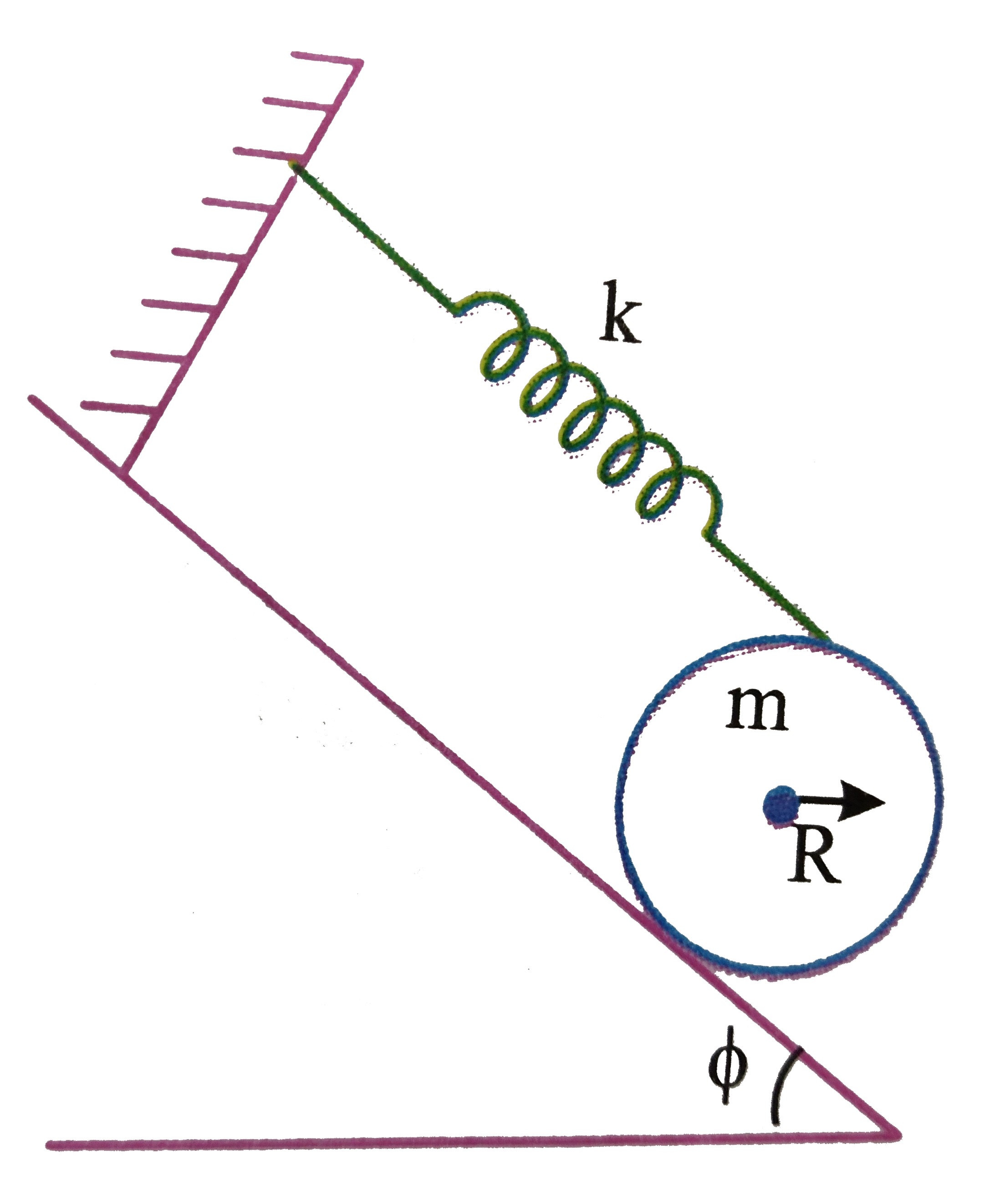
A uniform cylinder of mass m and radius R is in equilibrium on an inclined plane by the action of a light spring of stiffness k, gravity and reaction force acting on it. If the angle of inclination of the plane is ϕ, then angular frequency of small oscillations of the cylinder is...........
2√km
2√2km
2√2k3m
√2km
The correct Answer is:C
Let, x be the displacement of centre of mass of cylinder from mean position.
∴ from rolling concept, elongation in spring =2x
∴ Restoring torque about point of contact is:
τrest=−2R(2kx)=−4kxR
but x=Rθ⇒τrest=−4kR2θ=Iα
=32mR2.α and α=−ω2θ :
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-I
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage
Explore 33 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
A uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffness, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
A uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
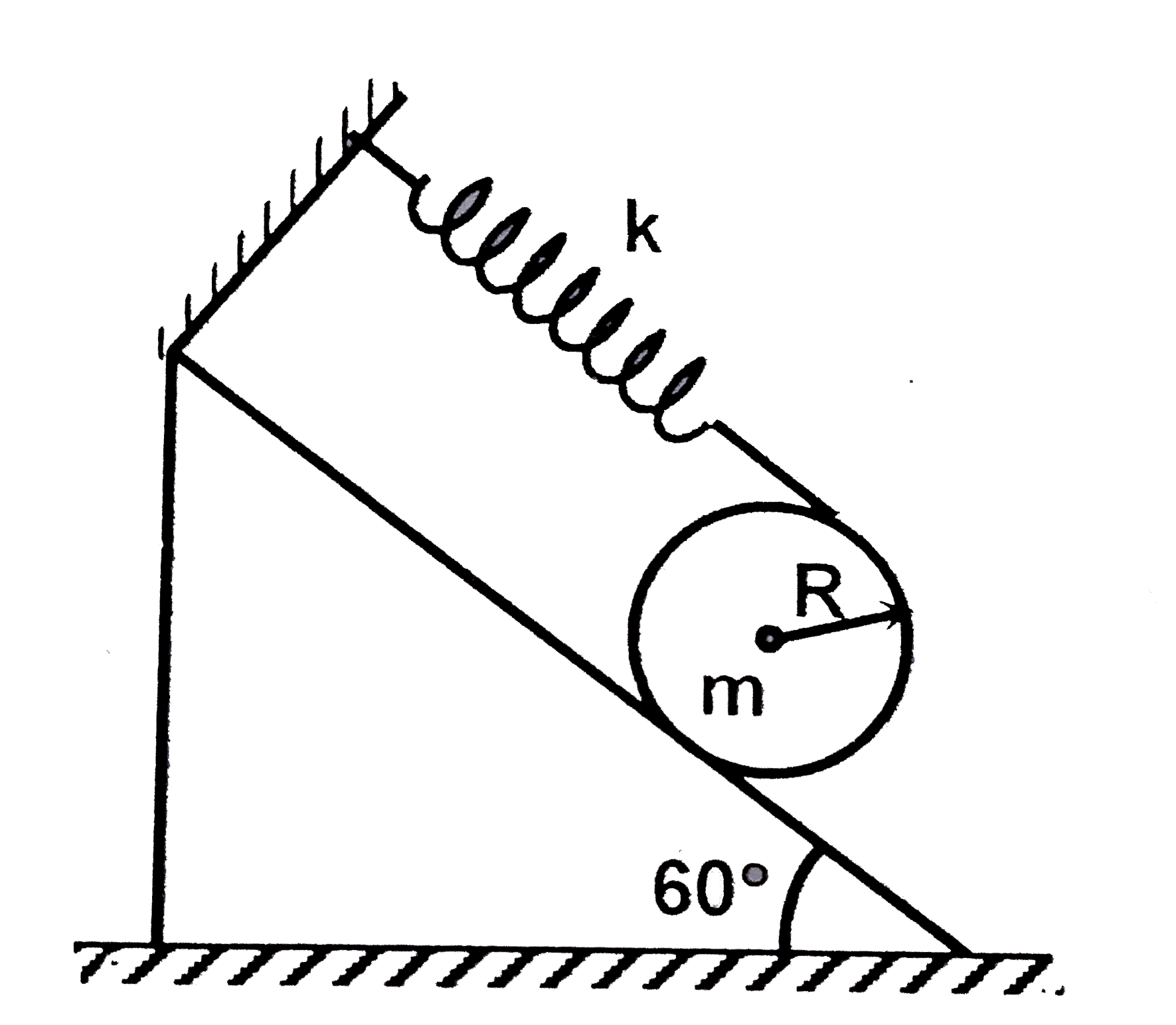 A2π√m10kB2π√7m10kC2π√7m20kD2π√7m40k
A2π√m10kB2π√7m10kC2π√7m20kD2π√7m40kA cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
A12Mv2B12Iω2C34Mv2D34Iω2A cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
A12Mv2B12Iω2C34Mv2D34Iω2
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding.
x
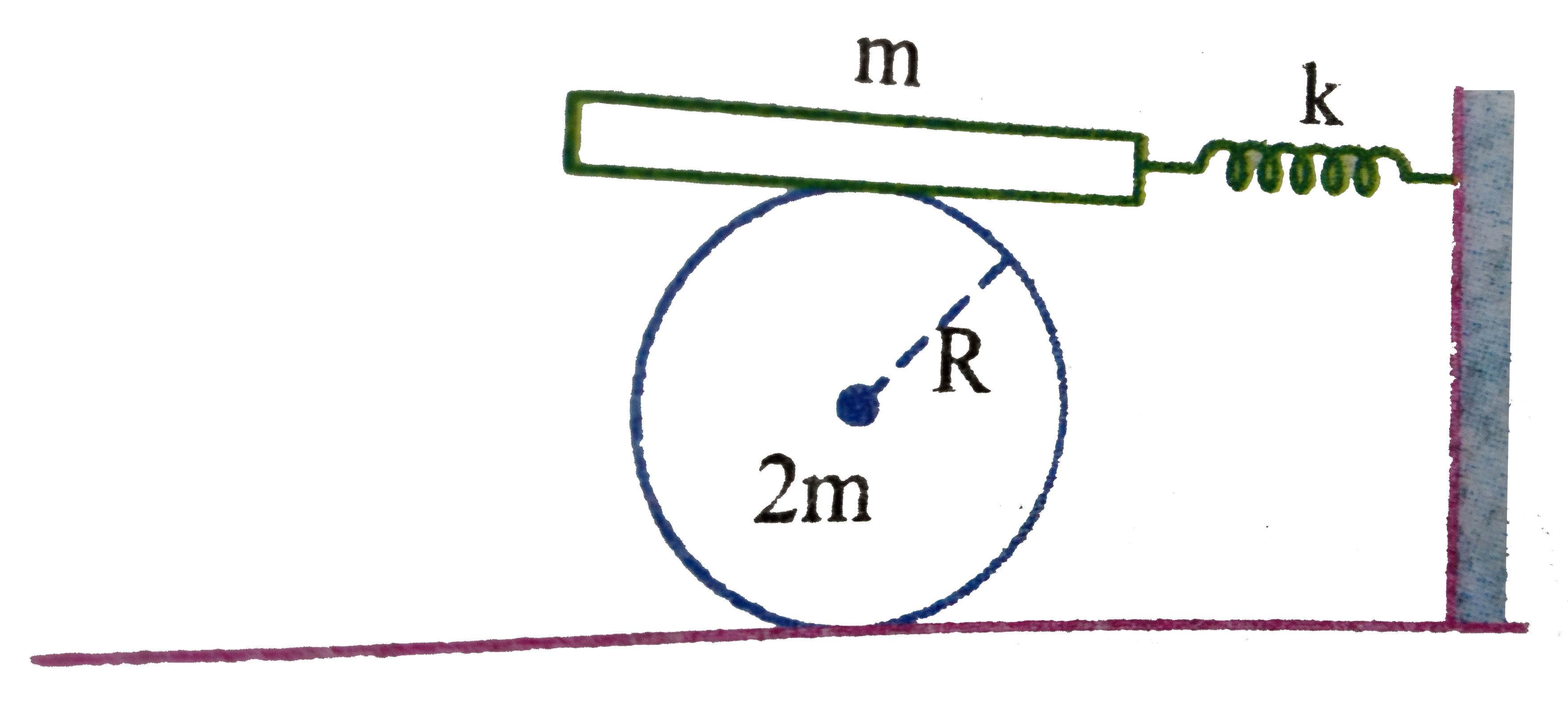
View SolutionA uniform plank of mass m=1kg, free to move in the horizontal direction only, is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attched to a fixed wall by means of light spring of spring constant k=7N/m2. There is no slipping between the cylinder and the plank, and between the cylinder and the ground. the angular frequency of small oscillations of the system is
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View Solution

