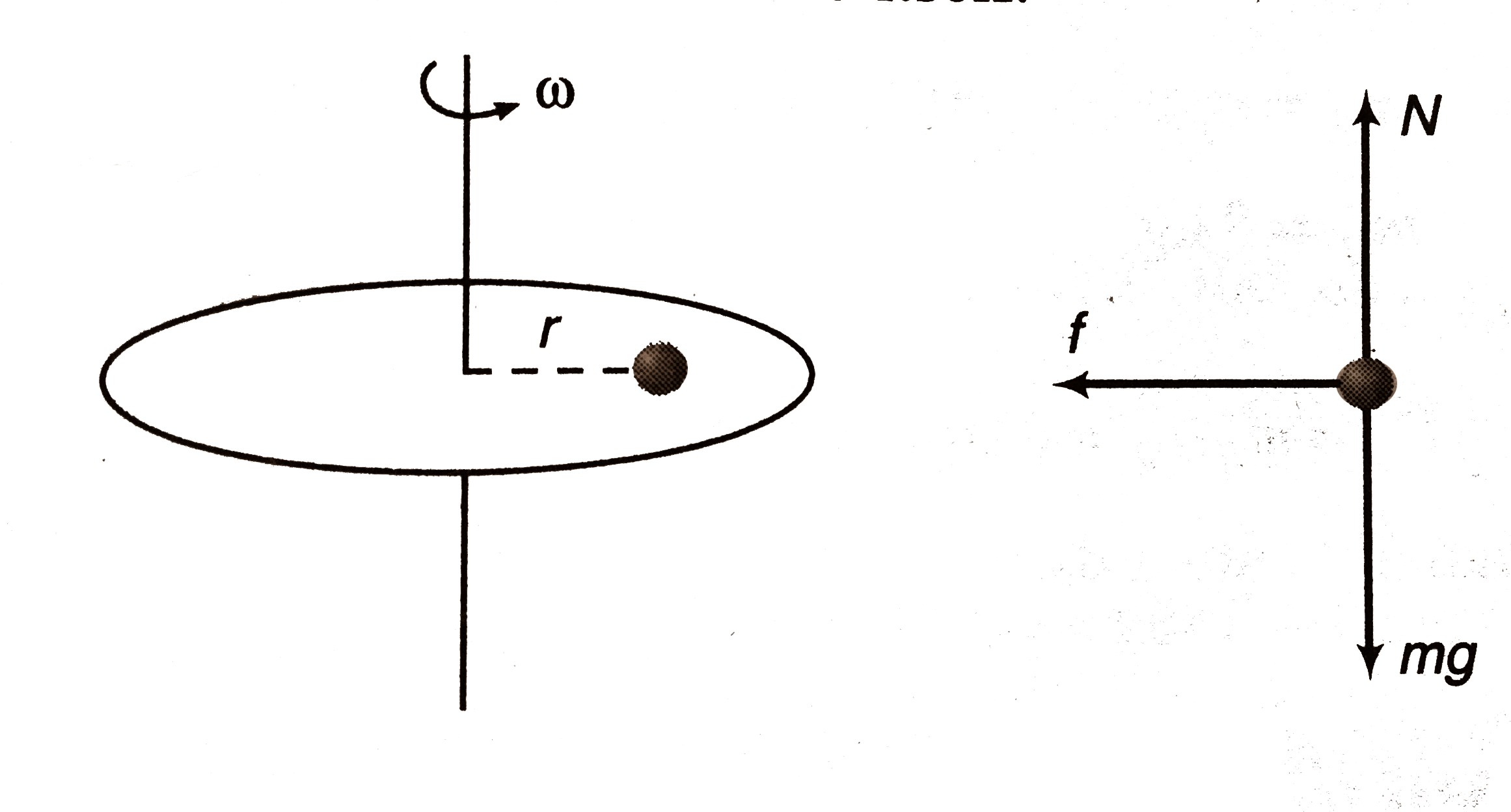
A particle of mass m is placed over a horizontal circular table rotati

A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A horizontal disk is rotating with angular velocity $ω$ about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

A $\frac{\sqrt{3}}{2} ω R$
B $\frac{ω R}{2}$
C $ω R$
D $\frac{ω R}{\sqrt{2}}$
A rough horizontal plate rotates with angular velocity $ω$ about a fixed verticle axis. A particle or mass $m$ lies on the plate at a distance $\frac{5 a}{4}$ from this axis. The coefficient of friction between the plate and the particle is $\frac{1}{3}$ . The largest value of $ω^{2}$ for which the oparticle will continue to be at rest on the revolving plate is
A $\frac{g}{3 a}$
B $\frac{4 g}{5 a}$
C $\frac{4 g}{9 a}$
D $\frac{4 g}{15 a}$

A particle of mass $m$ is placed over a horizontal circular table rotating with an angular velocity $ω$ about a vertical axis passing through its centre. The distance of the object from the axis is $r$ . Find the force of friction $f$ between the particle and the table.