A sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R(figure). The system is set in rotation with a constant angular velocity ω about a vertical axis OO′. Find the angle θ corresponding to the steady position of the sleeve.
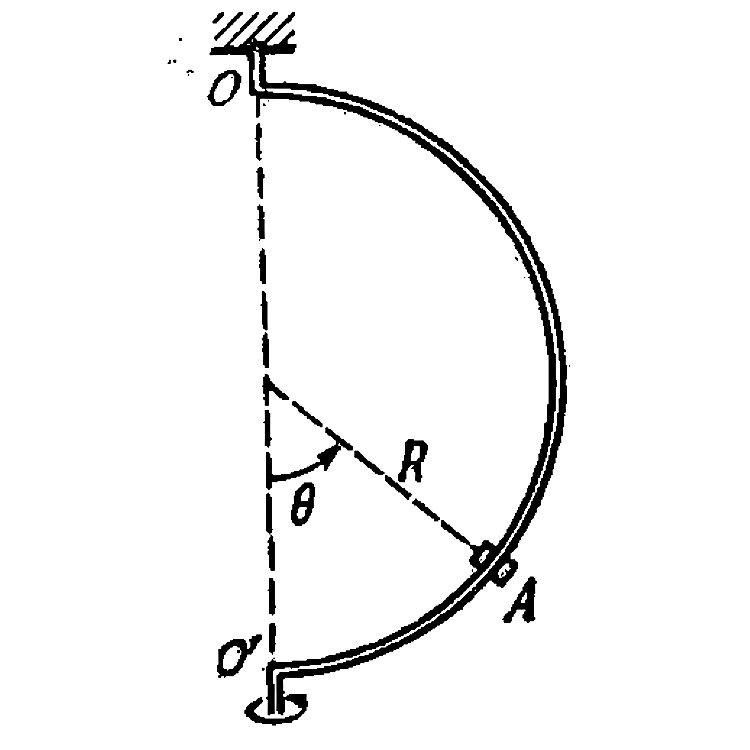
There are two forces on the sleeve, the weight F1 and the centrifugal force F2. We resolve both forces into tangential and normal component then the net downward tangential force on the sleeve is,
mgsinθ(1−ω2Rgcosθ)
This vanishes for θ=0 and for
θ=θ0=cos−1(gω2R), which is real if
ω2R>g. If ω2R<g, then 1−ω2Rgcosθ
is always positve for small values of θ and hence the net tangential force near θ=0 opposes any displacement away from it.
θ=0 is then stable.
If ω2R>g, 1−ω2Rgcosθ is negative for small
θ near θ=0 and θ=0 is then unstable.
However θ=θ0 is stable becuase the force tends to bring the sleeve near the equilibrium position θ=θ0.
If ω2R=g, the two positions coincide and becomes a stable equilibrium point.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A sleeve A can slide freely along a smooth rod bent in the shape of a half circle of radius R .The system is set in rotaion with a constant angular velocity ω about a vertical axis OO' .Find the angle θ corresponding to the steady position of the sleeve

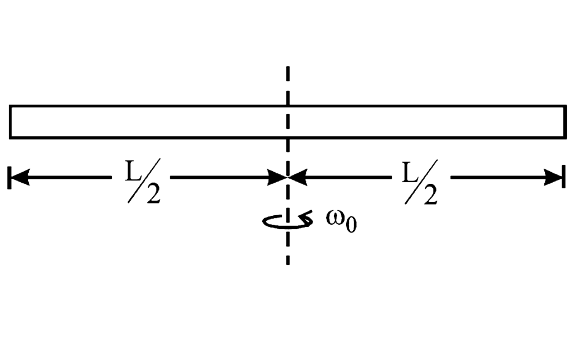
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beada are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpenducular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
View Solution
Knowledge Check
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 Aω0BMω0M+12mCMω0M+2mDMω0M+6m
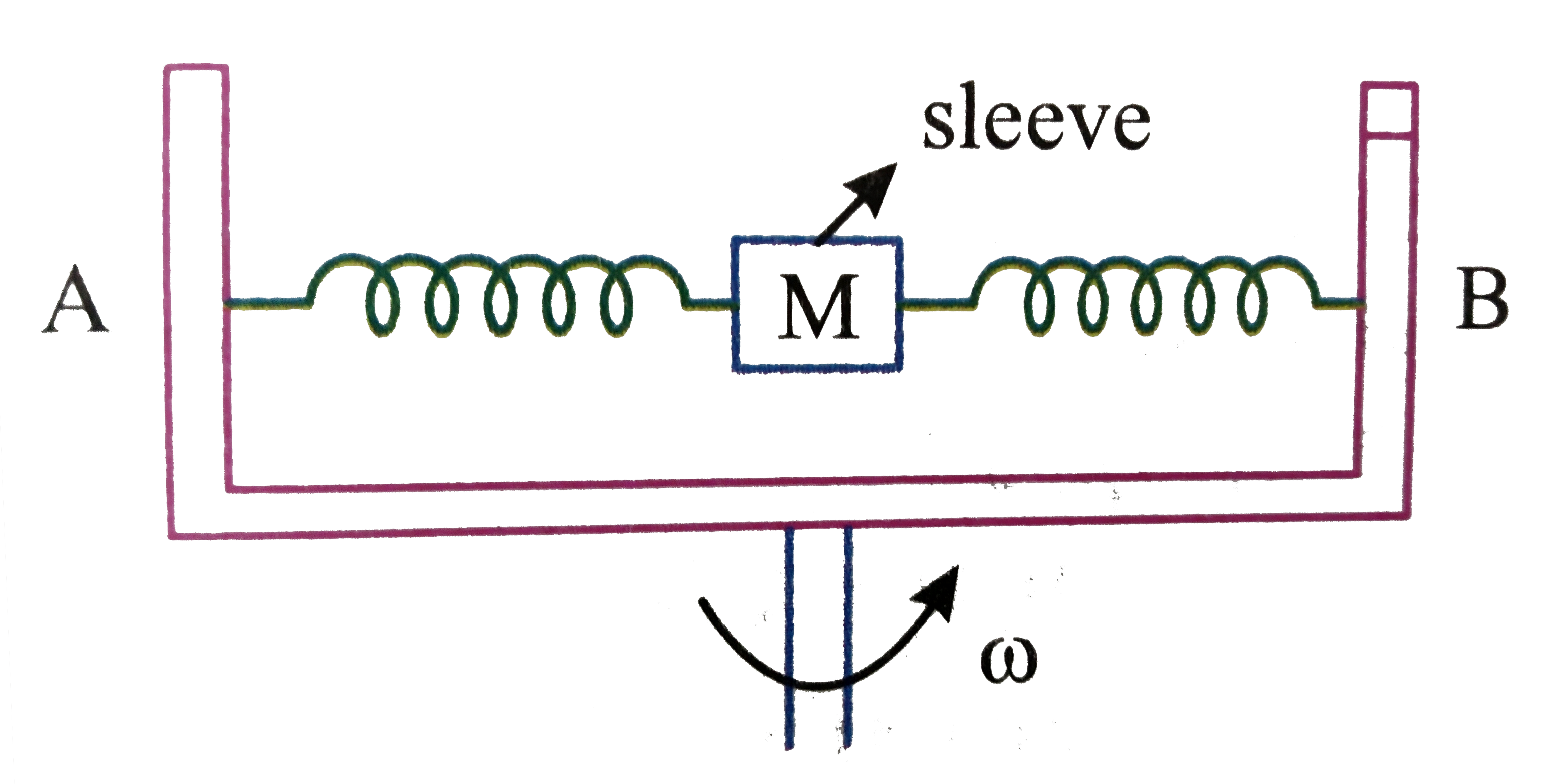
Aω0BMω0M+12mCMω0M+2mDMω0M+6mIn the arrangement shown, the sleeve of mass M is fixed between two identical springs whose combined force constant is k. The sleeve can slide without friction over a horizontal bar AB. The arragement rotates with a constant angular velocity ω about a vertical axis passing through the middle of the bar. the period of small oscillations of teh sleeve is.........
 A2π√mkB2π√mk−mω2Cπ√mkDπ√mk−mω2
A2π√mkB2π√mk−mω2Cπ√mkDπ√mk−mω2A rope of mass'm' is looped in a circle of radius R and rotated with a constant angular velocity about its axis in gravity free space . Find the tension in the rope ?
AT=mRω20B2mRπω2CT=mRπω202πD4mRπω20
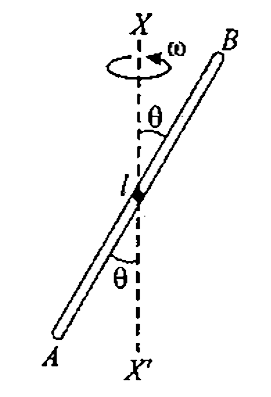
Find total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity ω , about a vertical axis XX', shown in figure .
View SolutionIn the arrangement shown in figure the sleeve M of mass m=0.20kg is fixed between two identical springs whose combined stiffness is equal to x=20N/m. The sleeve can slide without friction over a horizontal bar AB. The arrrangement rotates with a constant angular velocity ω=4.4rad/s about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve ?
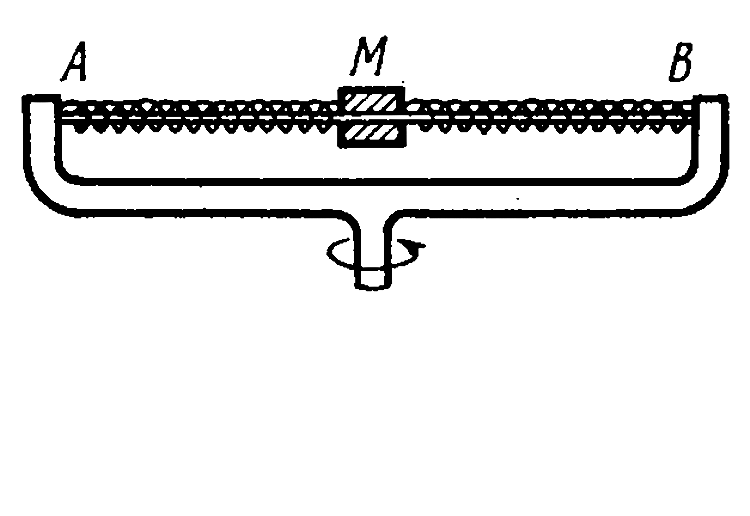
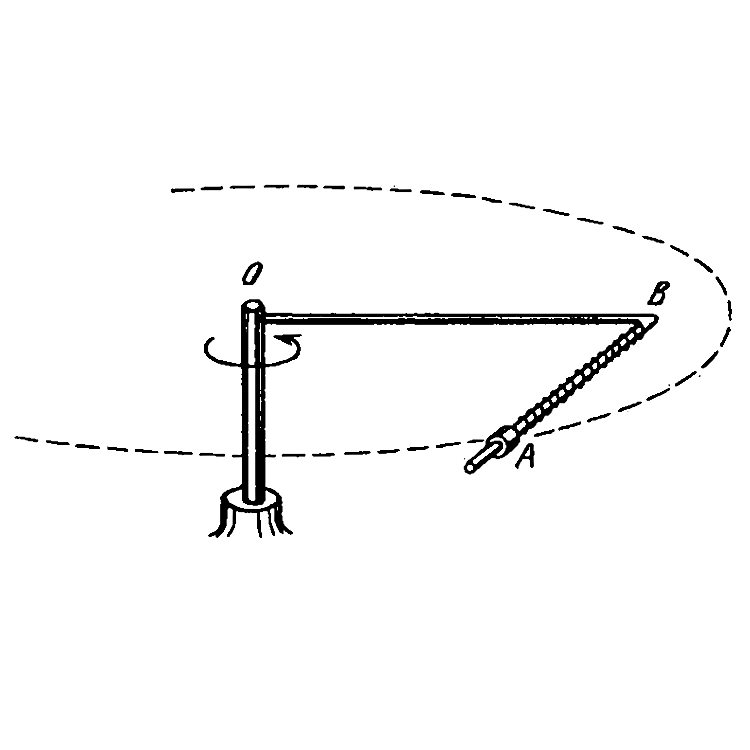
View SolutionA device (figure) consists of a smooth L-shaped rod located in a horizontal plane and a sleeve A of mass m attached by a weight less spring to a point B. The spring stiffness is equal to x. The whole system rotates with a constant angular velocity ω about a vertical axis passing through the point O. Find the elongation of the spring. How is the result affected by the rotation direction?
View SolutionA chain of mass m forming a circle of radius R is slipped on a smooth round cone with half- angle θ. Find the tension in the chain if it rotates with a constant angular velocity ω about a vertical axis coinciding with the symmetry axis of the cone .
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View Solution

