A ring of mass $m$ and radius $R$ is being rotated about its axis with constant angular velocity $ω$ in the gravity free space. Find tension in the ring.

Video Solution

Text Solution

Verified by Experts

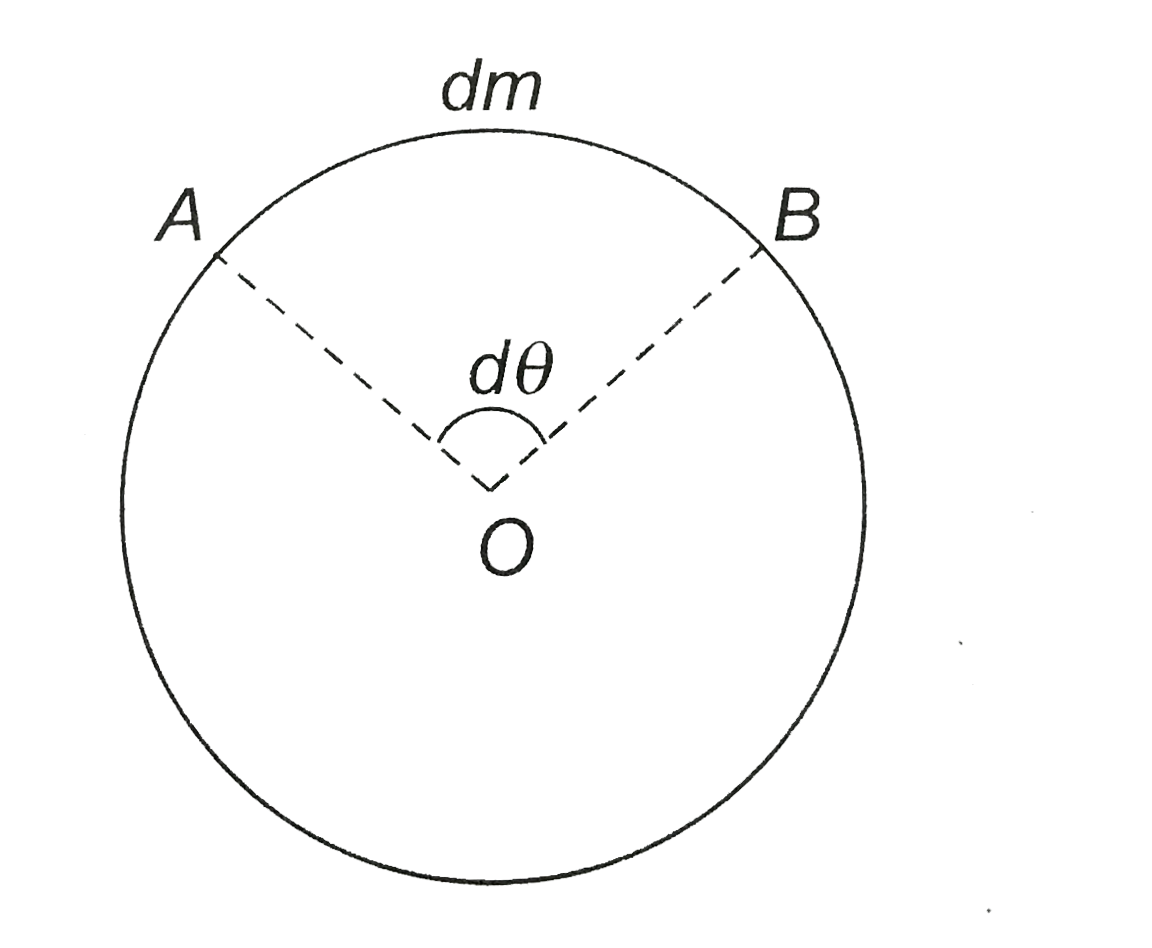
Consider a small length of ring that subtends an angle $d θ$ at the center.
$d m = \frac{m}{2 π R} d l = \frac{m}{2 π R} R d θ = \frac{m}{2 π} d θ$
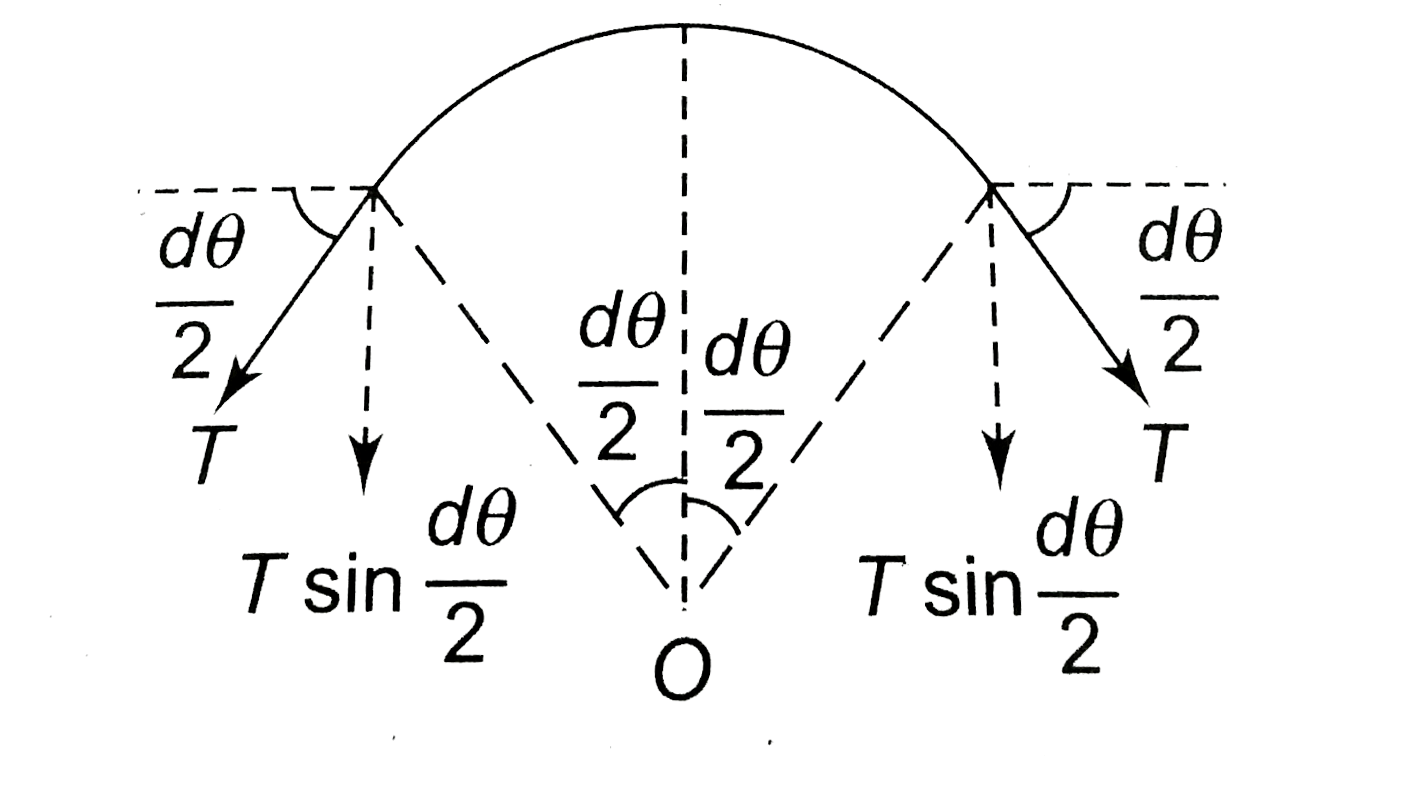
$d m$ is moving in the circle and the necessary centripetal force is provide by component of tension.
$2 T sin (\frac{d θ}{2}) = d m ω^{2} R = \frac{m ω^{2} R}{2 π} d t h η$
As $d θ$ is small
$sin (\frac{d θ}{2})$
$2 T \frac{d θ}{2} = T \times d θ = \frac{m ω^{2} R}{2 π} d θ$
$T = \frac{m ω^{2} R}{2 π}$

|

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity $ω$ . The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
A $\frac{ω M}{(m + M)}$
B $\frac{ω (M - 2 M)}{(M + 2 m)}$
C $\frac{ω M}{(M + 2 m)}$
D $\frac{ω (M + 2 m)}{M}$
Question 2 - Select One
A thin circular ring of mass $m$ and radius $R$ is rotating about its axis with a constant angular velocity $ω$ . Two objects each of mass $M$ are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity $ω' =$
A $\frac{ω (m + 2 M)}{m}$
B $\frac{ω (m - 2 M)}{(m + 2 M)}$
C $\frac{ω m}{(m + M)}$
D $\frac{ω m}{(m + 2 M)}$
Question 3 - Select One
A thin circular ring of mass M and radius r is rotating about its axis with constant angular velocity $ω$ . Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring . The ring now rotates with angular velocity given by
A $\frac{(M + 2 m) ω}{2 m}$
B $\frac{2 M ω}{M + 2 m}$
C $\frac{(M + 2 m) ω}{M}$
D $\frac{M ω}{M + 2 m}$

CP SINGH-CIRCULAR MOTION-Exercise

Home
Ask Doubt
Profile