An object moves at a constant speed along a circular path in a horizontal XY plane, with the center at the origin. When the object is at x=−2m, its velocity is −(4m/s)ˆj. What is the object's acceleration when it is y=2m
−(8m/s2)→j
−(8m/s2)→i
−(4m/s2)→j
−(4m/s2)→i
The correct Answer is:B
To solve the problem step by step, we need to analyze the motion of the object moving in a circular path and determine its acceleration when it is at a specific position.
Step 1: Understand the motion
The object is moving in a circular path with a constant speed. The center of the circular path is at the origin (0,0) in the XY plane.
Step 2: Identify the given information
- When the object is at x=−2m, its velocity is −4ms in the −j direction (downward).
- We need to find the acceleration when the object is at y=2m.
Step 3: Determine the radius of the circular path
Since the object is at x=−2m, we can find the radius of the circular path. The distance from the center (origin) to this point is:
\( r = \sqrt{(-2)^2 + 0^2} = 2 \text{ m} \)
Step 4: Calculate the speed
The speed of the object is given as 4ms. This speed remains constant as the object moves along the circular path.
Step 5: Use the formula for centripetal acceleration
The formula for centripetal acceleration \( a \) is given by:
\( a = \frac{v^2}{r} \)
where:
- \( v \) is the speed of the object,
- \( r \) is the radius of the circular path.
Step 6: Substitute the known values
Substituting the values we have:
- \( v = 4 \text{ m/s} \)
- \( r = 2 \text{ m} \)
Calculating the acceleration:
\( a = \frac{(4 \text{ m/s})^2}{2 \text{ m}} = \frac{16 \text{ m}^2/\text{s}^2}{2 \text{ m}} = 8 \text{ m/s}^2 \)
Step 7: Determine the direction of acceleration
In circular motion, the acceleration is directed towards the center of the circular path. Since the object is at y=2m, the center is at the origin (0,0), which means the acceleration vector points in the negative j direction (downward).
Step 8: Write the final answer
Thus, the acceleration of the object when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
Final Answer:
The object's acceleration when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
---
The object is moving in a circular path with a constant speed. The center of the circular path is at the origin (0,0) in the XY plane.
- When the object is at x=−2m, its velocity is −4ms in the −j direction (downward).
- We need to find the acceleration when the object is at y=2m.
Since the object is at x=−2m, we can find the radius of the circular path. The distance from the center (origin) to this point is:
\( r = \sqrt{(-2)^2 + 0^2} = 2 \text{ m} \)
The speed of the object is given as 4ms. This speed remains constant as the object moves along the circular path.
The formula for centripetal acceleration \( a \) is given by:
\( a = \frac{v^2}{r} \)
where:
- \( v \) is the speed of the object,
- \( r \) is the radius of the circular path.
Substituting the values we have:
- \( v = 4 \text{ m/s} \)
- \( r = 2 \text{ m} \)
\( a = \frac{(4 \text{ m/s})^2}{2 \text{ m}} = \frac{16 \text{ m}^2/\text{s}^2}{2 \text{ m}} = 8 \text{ m/s}^2 \)
In circular motion, the acceleration is directed towards the center of the circular path. Since the object is at y=2m, the center is at the origin (0,0), which means the acceleration vector points in the negative j direction (downward).
Thus, the acceleration of the object when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
The object's acceleration when it is at y=2m is:
\( \mathbf{a} = -8 \hat{j} \text{ m/s}^2 \)
Topper's Solved these Questions
Similar Questions
An object moves at constant speed along a cicular path in a horizontal xy plane. With the centre as origin.when the object is at x= -2m , it s velocity is −4ˆjm/s , its acceleration when it is at y= 2 m/s
View SolutionAn object moves counter−clockwise along the circular path shown below. As it moves along the path its acceleration vector continuously points towards point S. The object

View Solution
Knowledge Check
An object of mass m moves with constant speed in a circular path of radius r under the action of a force of constant magnitude F. the kinetic energy of object is
A12FRBFRC2FRD14FRWhat is the momentum of an object of mass m , moving with a velocityv ?
A(mv)2Bmv2C12mv2DmvWhen an object is moving with a uniform velocity, what is its acceleration?
ANon-uniformBNegativeCPositiveDzero
A point object moves in + x-direction with v= 1 m/s along the principal axis of the concave mirror of focal length f=10 m. When the mirror moves with a velocity Vm=−ˆi m/s and the object is at a distance of p=15 m, the speed of the image is -
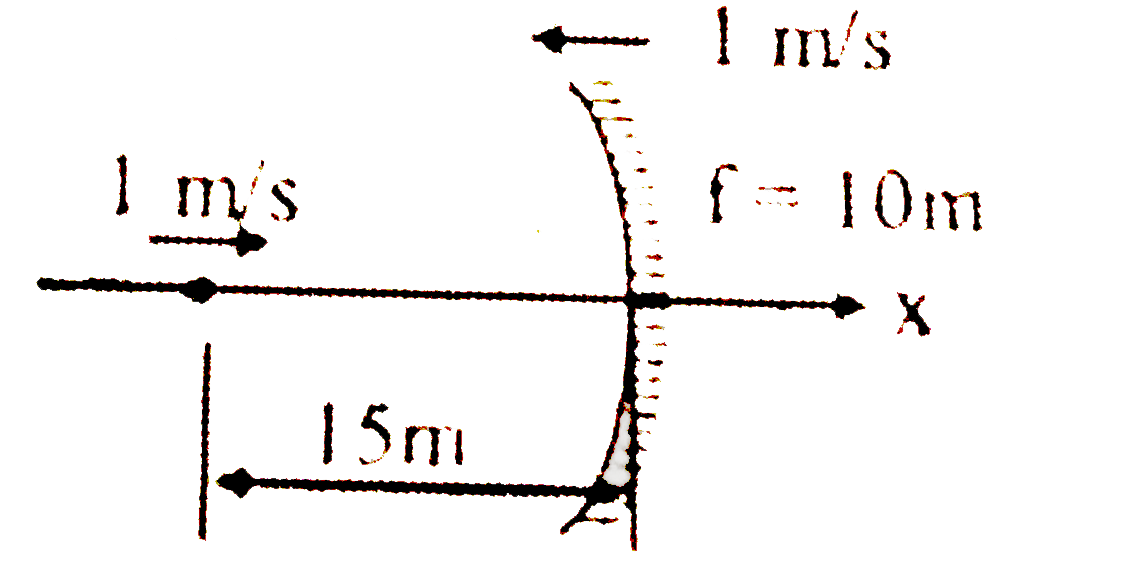
View SolutionAn object moves 10 m in 4 s then turns left and moves 20 m in next 5 s. What is the average speed of the object?
View SolutionAn electron moves along a circular path of radius 10 cm. If the centripetal acceleration is 4×1011m/s2 , then its linear speed is
View SolutionAn object is moving in x−y plane its velocity and acceleration at t=0 are represented in figure.

After how much time object crosses the y−axis:-
View SolutionA particle is moving along a circular path in xy-plane.When its crosses x-axis,it has an acceleration along the path of 1.5m/s2, and is moving with a speed of 10m/s in −ve y-direction.The total acceleration is
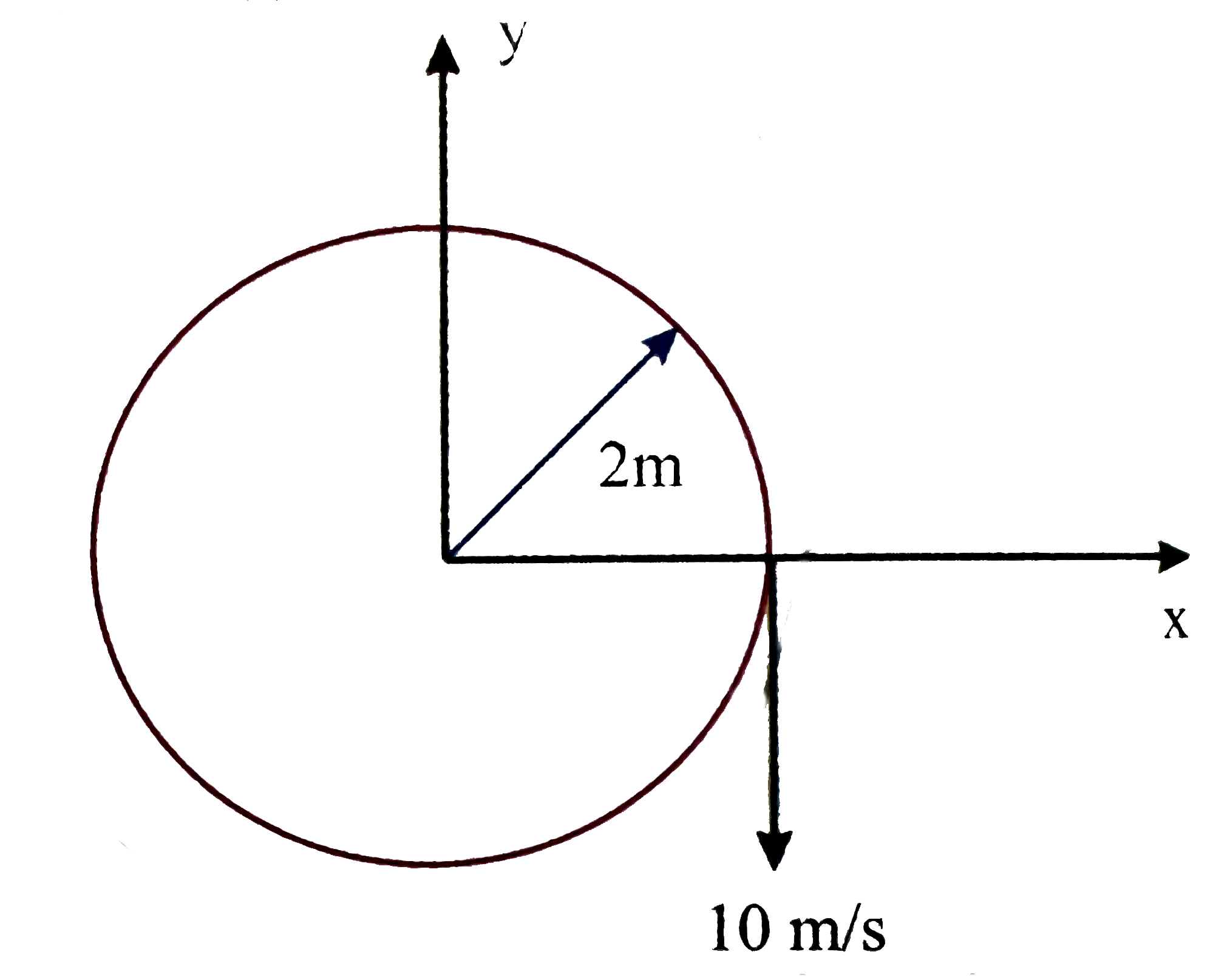
View Solution

