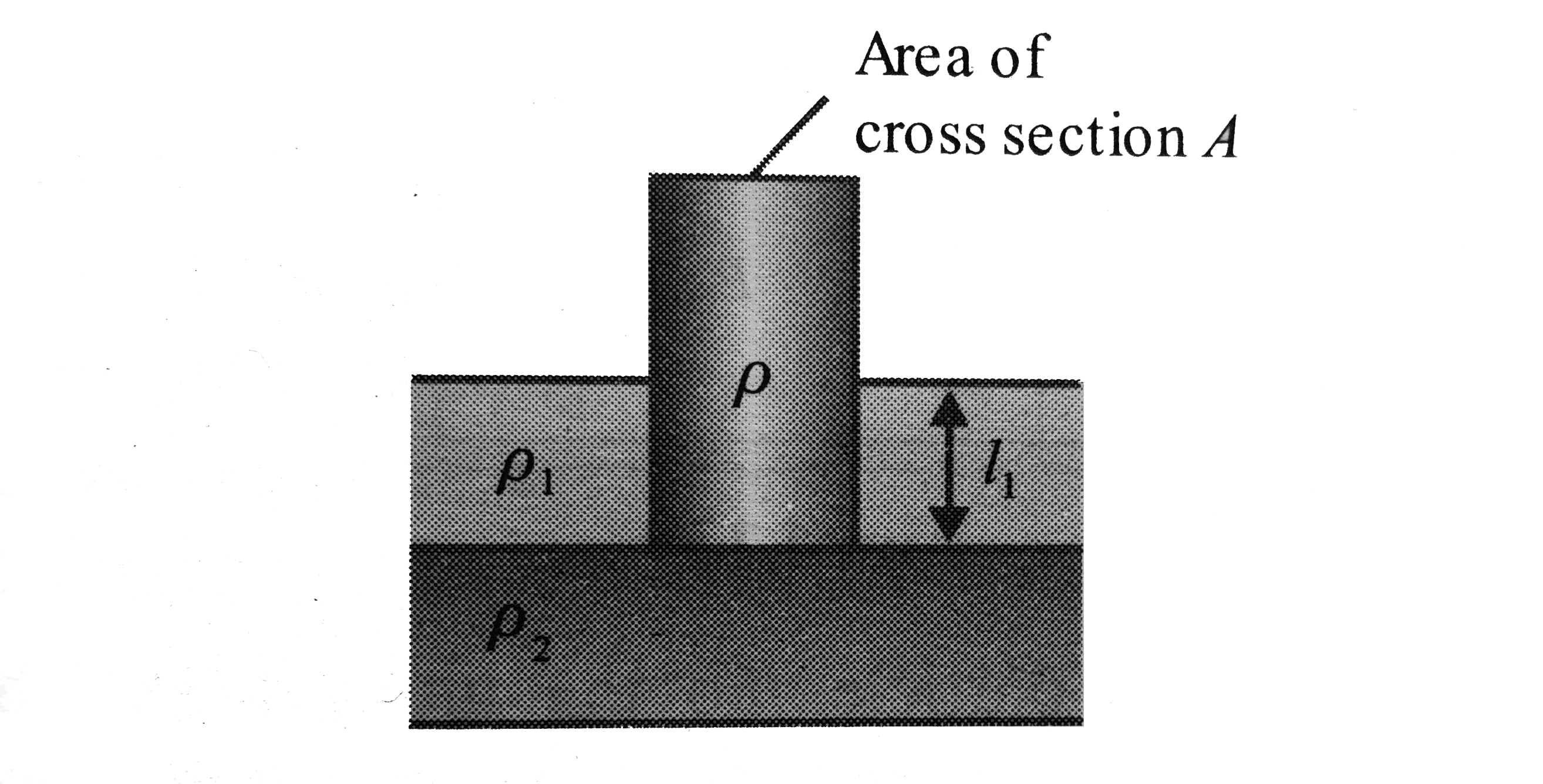
A vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
The correct Answer is:π[√ρlρ1g+√ρlρ2g]
In equation position , net force on pole is zero.
ρAlg=ρ1Al1g (i)
In displaced possition, net force.
F1=ρAlg−ρ1Al1g−ρ2Ayg=−Agy
Acceleration of the pole. a1=−ρ2AgρAly
Hence in the liquid of density r2.
ω1=√ρ2gρl⇒T1=2π√ρlρ2g
The pole system is in the liquid of density ρ2 for half time period only. When it moves in the liquid of density ρ1, the net force is F2=−ρAlg+(l1−y')Aρ1g=−ρ1Agy'
a2=−ρ2AgρAly'⇒ω2=√ρ1gρl
T2=2π√ρlρ1g
Total time period of oscillation of the cylinder is
T=T12+T22=π[√ρlρ1g+√ρlρ2g]
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
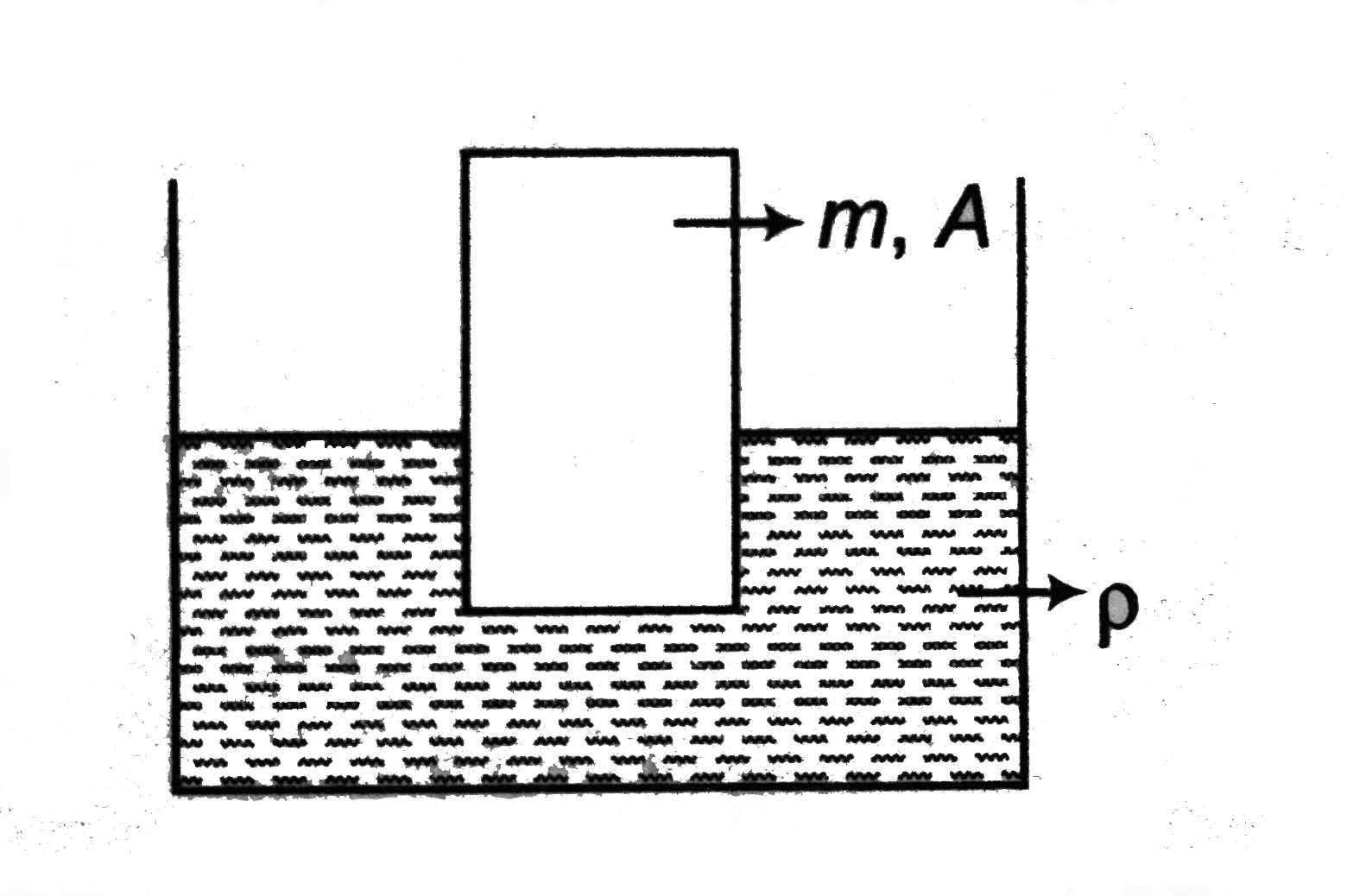
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionTwo immiscible liquids of densities ρ and 2ρ and thickness (heights) h and 2h, respectively, push a vertical plate. Find the total side thrust given by the liquids on the vertical plate.

View Solution
Knowledge Check
A vertical pole of length l, density ρ, area of cross section A, floats in two immiscible liquids of densities ρ1 and ρ2. In equilibrium position the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, the time period of oscillation is..........
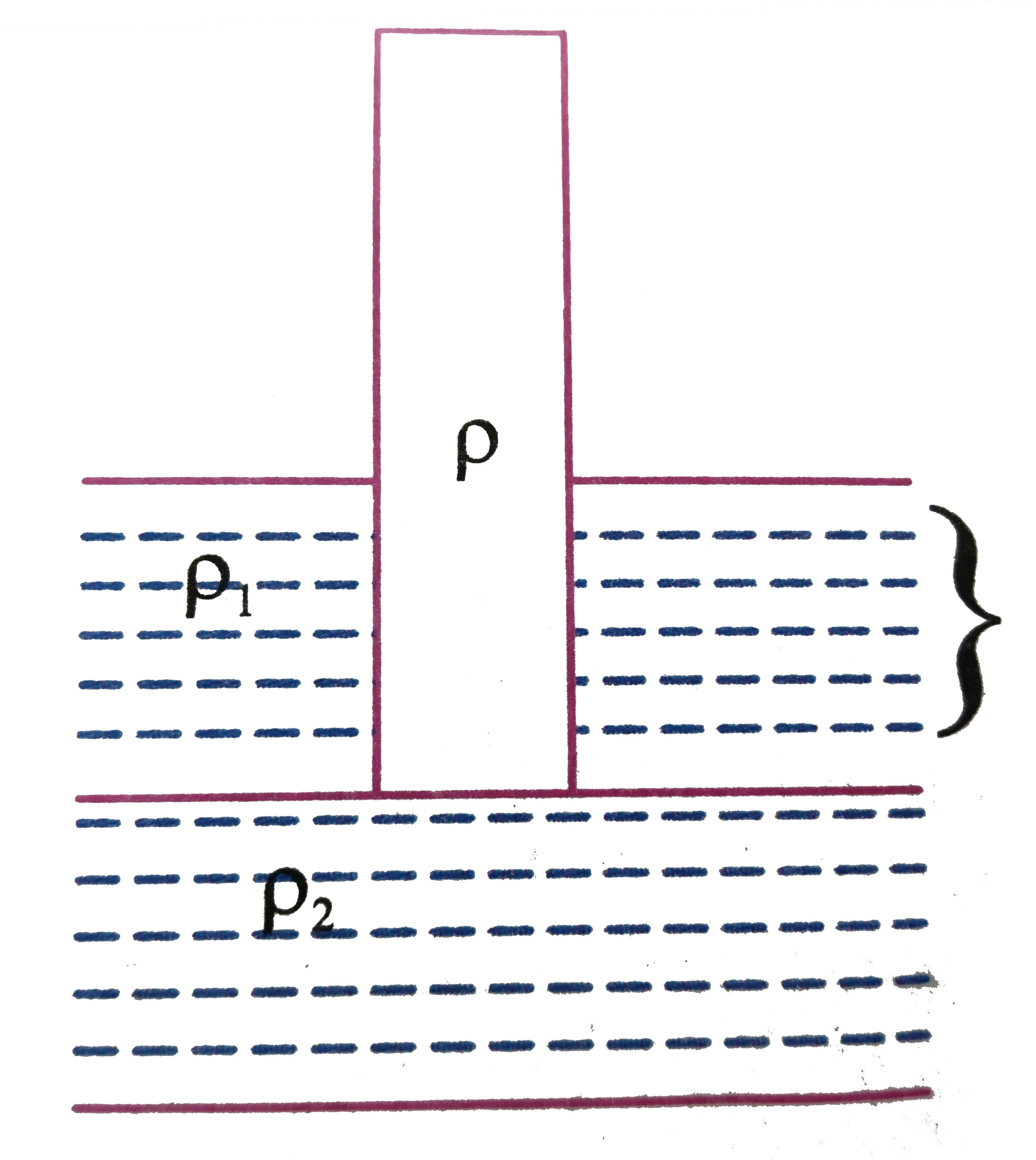 Aπ√ρl(ρ1+ρ2)gBπ√ρlg(1√ρ1+1√ρ2)Cπ√(ρ1+ρ2)lρgDπ√lρg(√ρ1+√ρ2)
Aπ√ρl(ρ1+ρ2)gBπ√ρlg(1√ρ1+1√ρ2)Cπ√(ρ1+ρ2)lρgDπ√lρg(√ρ1+√ρ2)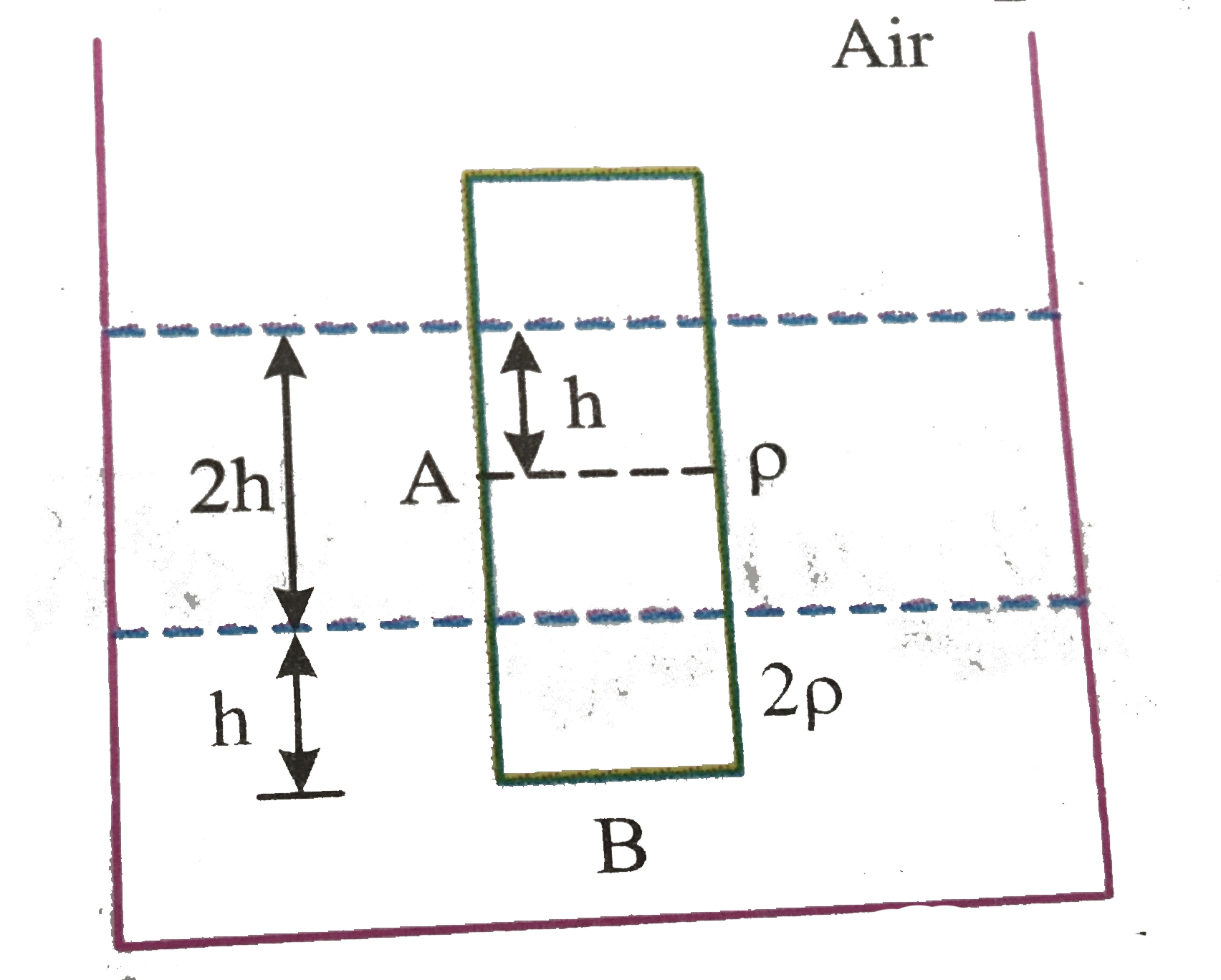
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:A2πghB3ρghC4ρghDnoneIf two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
Aρ=ρ1+ρ22Bρ=ρ1+ρ22ρ1ρ2Cρ=2ρ1ρ2ρ1+ρ2Dρ=ρ1ρ2ρ1+ρ2
If two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionA rectangular block of mass m and area of cross section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes with a time period T, then
View Solution