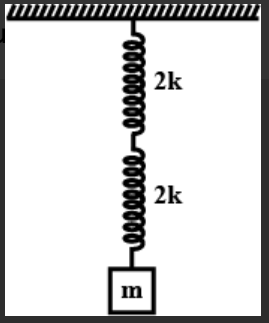
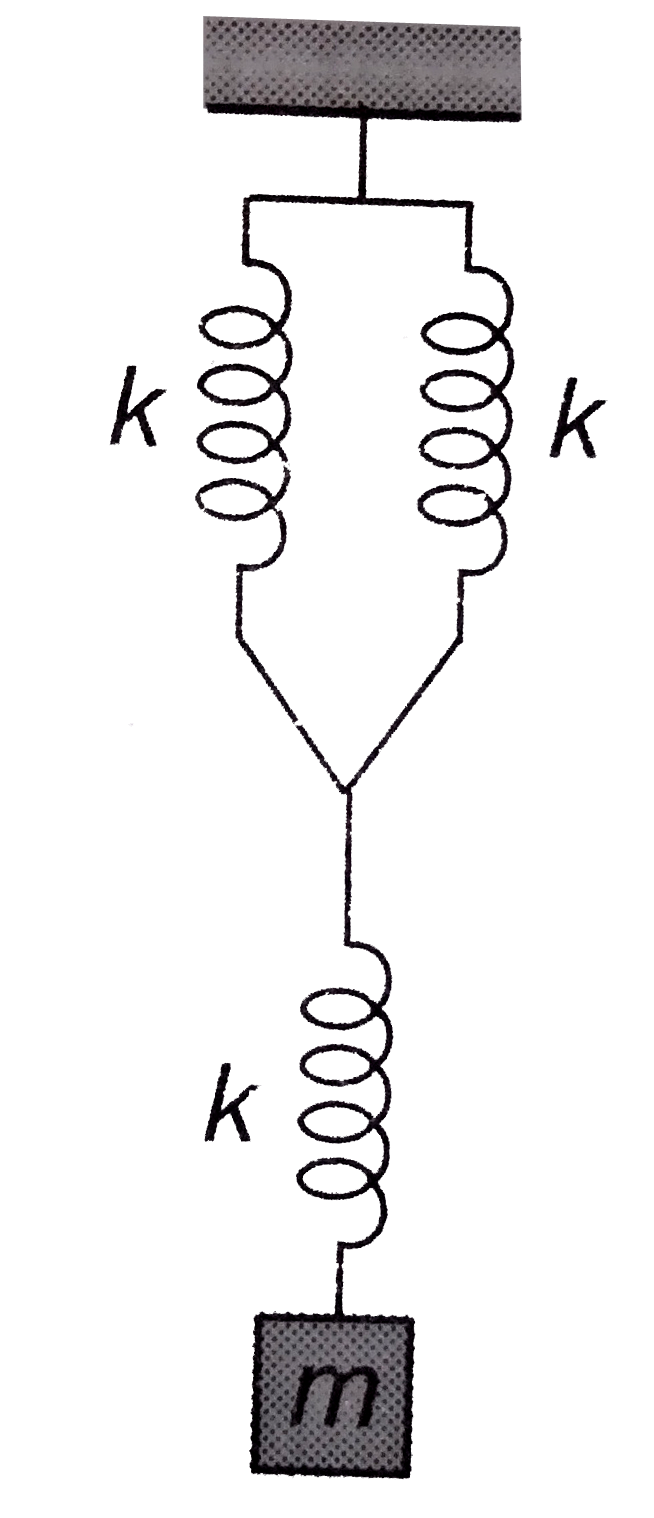
Disregading gravity, find the period of oscillation of the partical connected with four springs as shown in the figure.
(given:θ=45∘.Bη=30∘)

Video Solution
Text Solution
The correct Answer is:π√2mk
2ksin2θ=k1
or k1=2ksin2θ
and k2=2(2k)sin2β
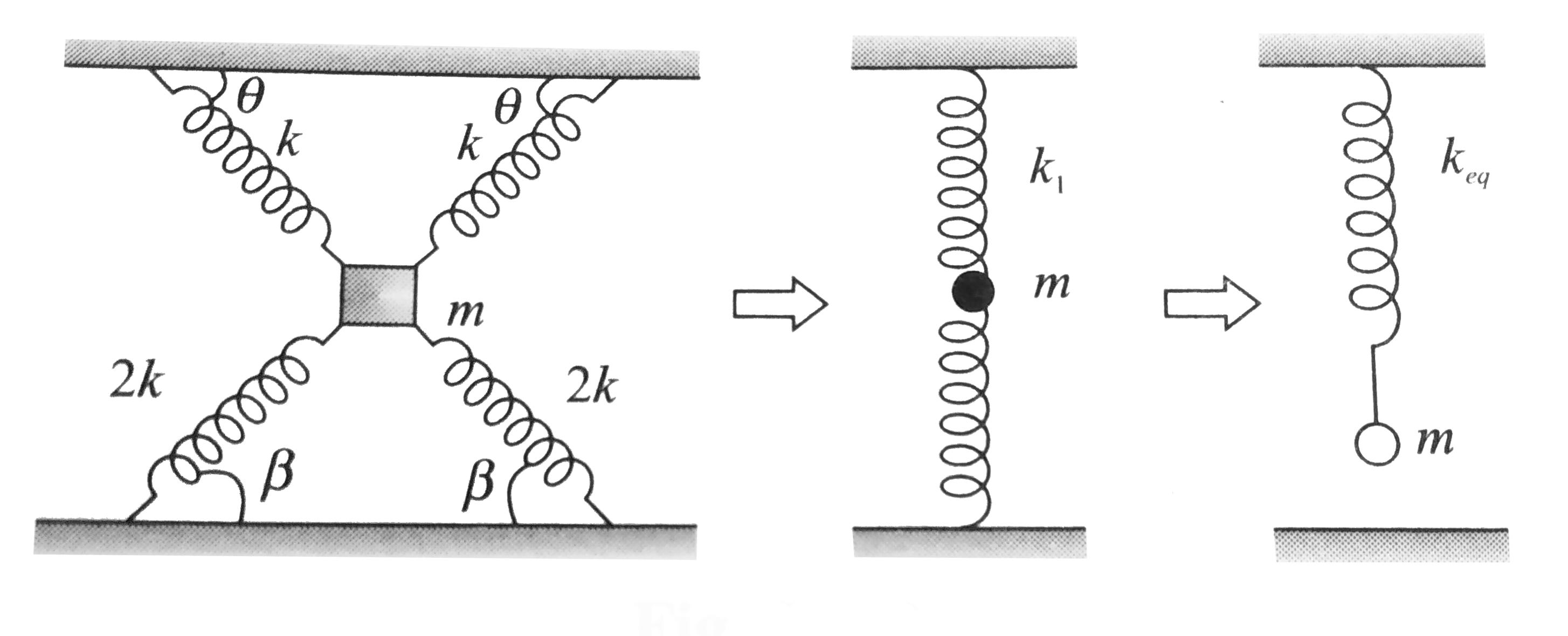
Then, keq=k1+k2=2k[sin2θ+2sin2β]
=2k[sin245∘+2sin230∘]=2k(12+12)=2k
Then T=2π√mkeq=2π√m2k=π√2mk
|
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single Correct
Explore 107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.2
Explore 23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Knowledge Check
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
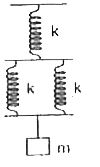 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmFour spring connect with mass as shown in figure. Find frequency of S.H.M.
 A12π√k4MB12π√4kMC12π√k7MD12π√7KM
A12π√k4MB12π√4kMC12π√k7MD12π√7KMFour spring connect with mass as shown in figure. Find frequency of S.H.M.
 A12π√k4MB12π√4kMC12π√k7MD12π√7KM
A12π√k4MB12π√4kMC12π√k7MD12π√7KM
Find the period of the oscillations of the devices shown in figure if m is displaced slightly.
View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
View SolutionThe frequency of oscillation of the springs shown in the figure will be

View SolutionThe frequency of oscillation of the spring shown in the figure will be
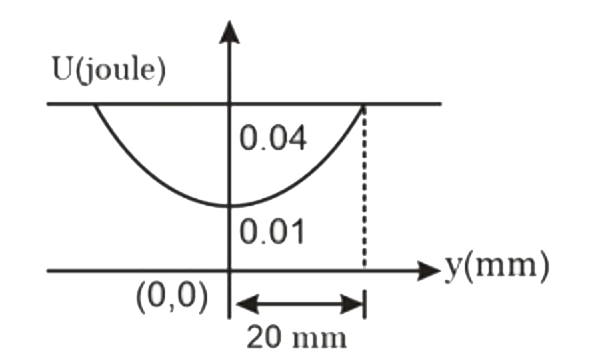
View SolutionThe variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is
View Solution