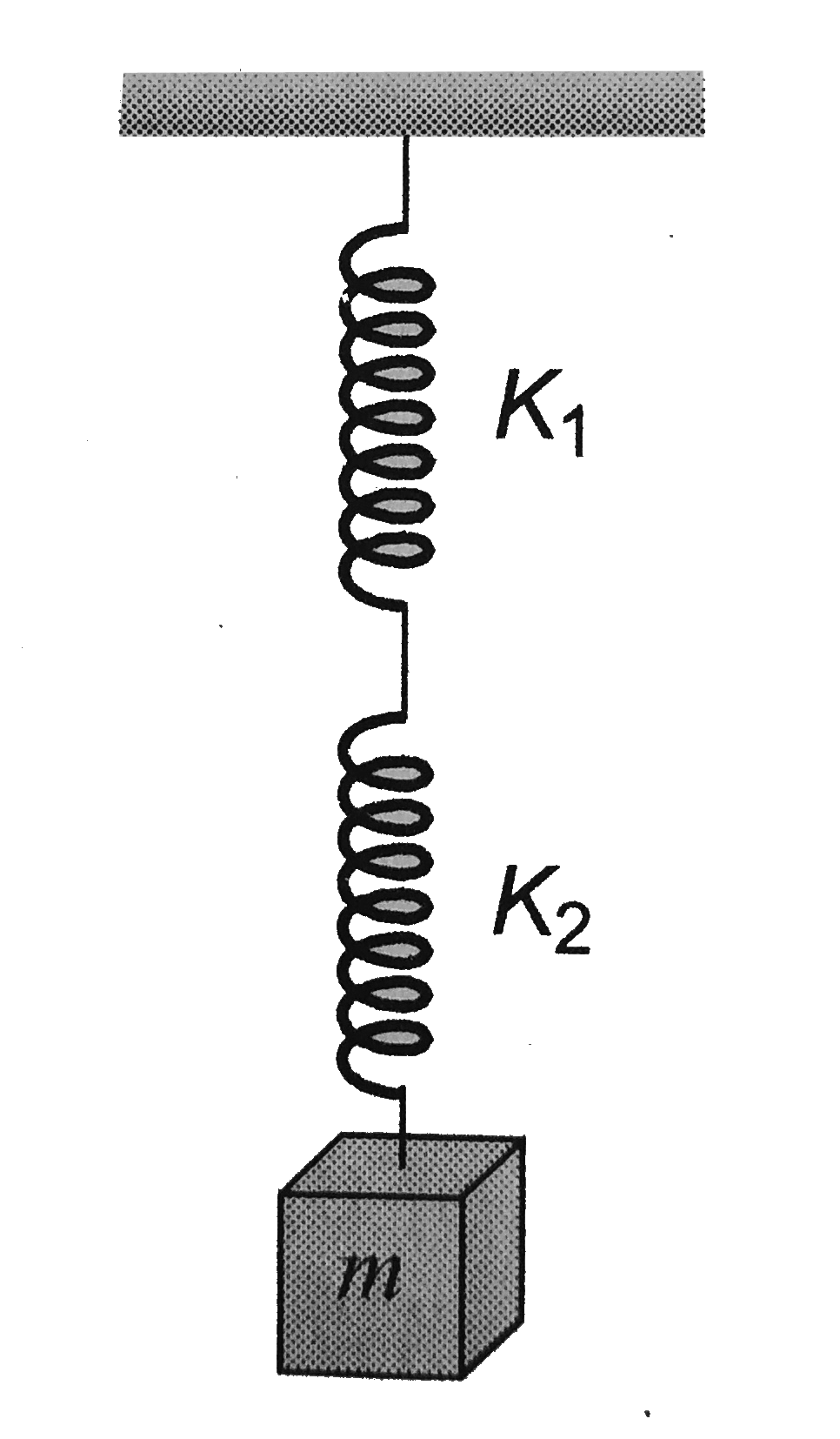
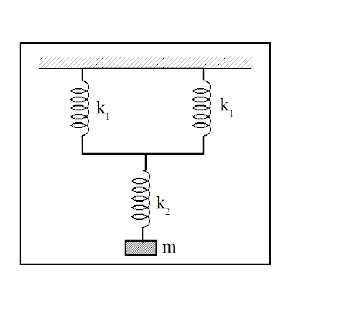
The frequency of oscillation of the spring shown in the figure will be
12π√Km
12π√(K1+K2)mK1K2
2π√Km
12π ⎷(K1K2m(K1+K2))
The correct Answer is:D
As spring are connected in series , effective force constant
1k=1k1+1k2⇒k=k1k2k1+k2
Hence frequency of oscillation is
n=12π√km=12π√k1k2(k1+k2)m
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:NEET Questions
Explore 39 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
The frequency of oscillation of the system shown in the figure will be
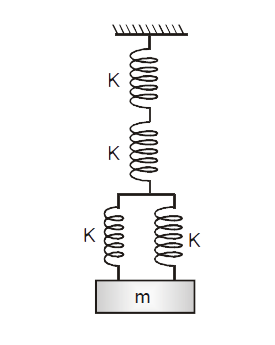
View SolutionFind the frequency of oscillations of the system in the figure. The bar is rigid and light.
[Hint: A spring of force constant k1 at a distance a is equivalent to a spring of force constant k1(ab)o2 at a distance b)

View Solution
Knowledge Check
The frequency of oscillation of the springs shown in the figure will be
 A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)
A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)Find the natural frequency of oscillation of the system as shown in figure. Pulleys are massless and frictionless. Spring and string are also massless. (Take π2=10)
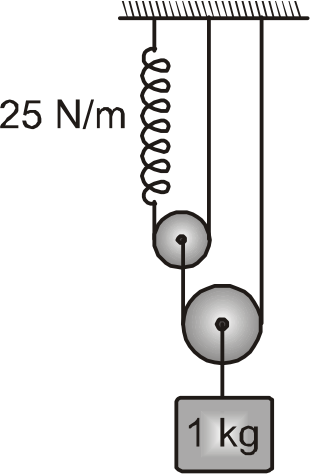 Aπ2HzB√πHzC10√πHzDπHz
Aπ2HzB√πHzC10√πHzDπHzIn figure S1 andS1 are identical springs. The oscillation frequency of the mass m is f. if one spring is removed, the frequency will become
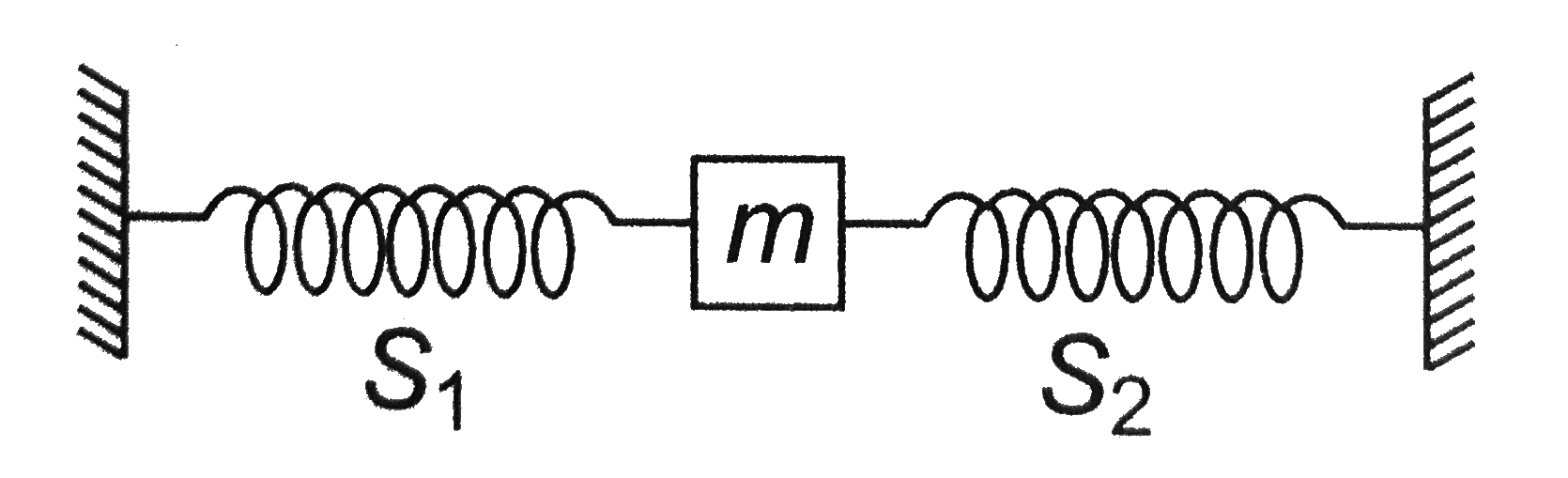 AfB2fC√2fDf√2
AfB2fC√2fDf√2
The time period of oscillation of the block as shown in figure is
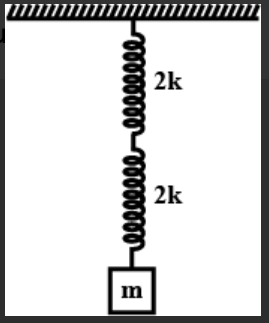
View SolutionFind the period of oscillation of the system shown in figure.

View SolutionThe total spring constant of the system as shown in the figure will be :
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionThe frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is

View Solution

