A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency $ω$ . The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time

at the mean position of the plateform

for an amplitude of $g^{2} / ω^{2}$

for an amplitude of $g / ω^{2}$

at the highest position of the plateform

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The net offect of these two forces must be toward mean position
At the mean position , there is no net and hence normal reaction equalls $m g$ Above position normal reaction is less than $m g$ and below mean position normal reaction is greater than $m g$ At the top extreme

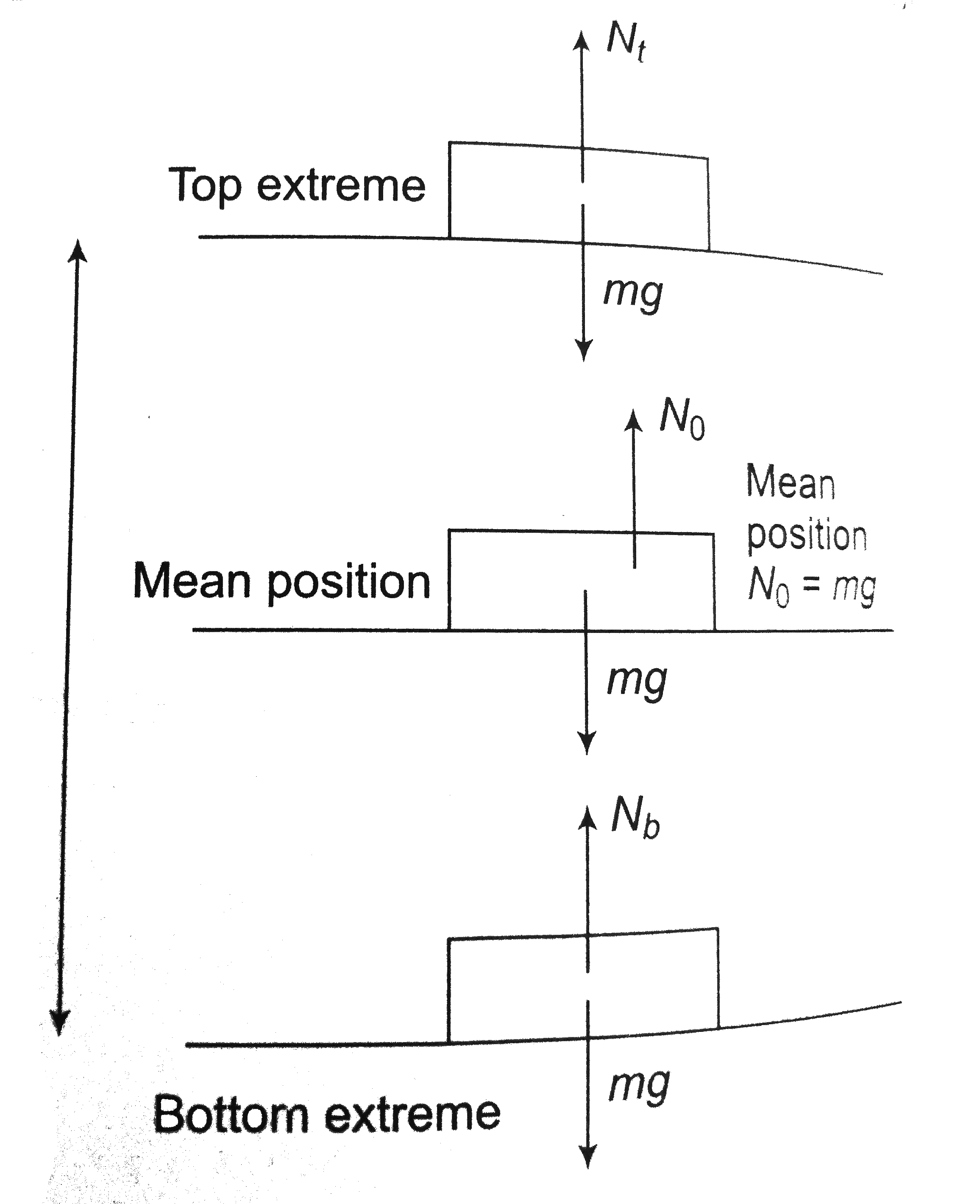
$N$ is minimum at the top exterme
Net fprce toward mean position $= m a = m ω^{2} A$
$\Rightarrow m g - N_{1} = m ω^{2} A$
$N_{1} = N_{min} = m g - m ω^{2} A$
For loosing contact with the plateform $N = 0$
so $A = g / ω^{2}$

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
In the previous question, the angular frequency of the simple harmonic motion is $ω$ . The coefficient of friction between the coin and the platform is $μ$ . The amplitude of oscillation is gradually increased. The coin will begin to slip on the platform for the first time
(i) at the extreme positions of oscillations
(ii) at the mean position
(iii) for an amplitude of $\frac{μ g}{ω^{2}}$
(iv) for an amplitude of $\frac{g}{μ ω^{2}}$
A(i),(iii)
B(ii), (iii)
C(i), (iv)
D(ii),(iv)
Question 2 - Select One
A coin is placed on a horizontal platform, which undergoes horizontal simple harmonic motion about a mean position O. The coin does not slip on the platform. The force of friction acting on the coin is F.
(i) F is always directed towards O
(ii) F is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
(iii) $F = 0$ when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
(iv) F is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
AF is always directed towards O
BF is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
C $F = 0$ when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
DF is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
Question 3 - Select One
A block of $0.5 k g$ is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of $0.5 H z$ . The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly
A $0.5 m$
B $0.75 m$
C $1 m$
D $1.2 m$

A2Z-OSCILLATION AND SIMPLE HARMONIC MOTION-AIIMS Questions

Home
Ask Doubt
Profile

A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of 0.5kg is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of 0.5Hz. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly

A2Z-OSCILLATION AND SIMPLE HARMONIC MOTION-AIIMS Questions

A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency $ω$ . The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time

A block of $0.5 k g$ is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of $0.5 H z$ . The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly