A horizontal platform vibrate up and down with a simple harmonic motion of amplitude 20 c.m. At what frequency will an object kept on the platform remain just in contact with the platform ? Take g=9.81m/s2.
To solve the problem of determining the frequency at which an object on a vibrating platform remains in contact with it, we can follow these steps:
Step 1: Understand the Problem
The platform vibrates with simple harmonic motion (SHM) and has an amplitude A=20cm=0.2m. The object will lose contact with the platform when the normal force acting on it becomes zero.
Step 2: Analyze Forces at the Highest Point
At the highest point of the platform's motion, the forces acting on the object are:
- The gravitational force downward: mg
- The normal force upward: N
For the object to just remain in contact with the platform, the normal force N must be zero. Thus, at the highest point:
N=mg−mω2A=0
This implies:
mg=mω2A
Step 3: Simplify the Equation
We can cancel the mass m from both sides (assuming m≠0):
g=ω2A
Step 4: Solve for Angular Frequency ω
Rearranging the equation gives us:
ω2=gA
Taking the square root, we find:
ω=√gA
Step 5: Substitute Values
Now, we substitute the values of g and A:
- g=9.81m/s2
- A=0.2m
Thus,
ω=√9.810.2=√49.05≈7rad/s
Step 6: Convert Angular Frequency to Frequency
The frequency f is related to angular frequency ω by:
f=ω2π
Substituting the value of ω:
f=72π≈76.2832≈1.11Hz
Final Answer
The frequency at which the object will remain just in contact with the platform is approximately:
f≈1.11Hz
---
The platform vibrates with simple harmonic motion (SHM) and has an amplitude A=20cm=0.2m. The object will lose contact with the platform when the normal force acting on it becomes zero.
At the highest point of the platform's motion, the forces acting on the object are:
- The gravitational force downward: mg
- The normal force upward: N
N=mg−mω2A=0
This implies:
mg=mω2A
We can cancel the mass m from both sides (assuming m≠0):
g=ω2A
Rearranging the equation gives us:
ω2=gA
Taking the square root, we find:
ω=√gA
Now, we substitute the values of g and A:
- g=9.81m/s2
- A=0.2m
ω=√9.810.2=√49.05≈7rad/s
The frequency f is related to angular frequency ω by:
f=ω2π
Substituting the value of ω:
f=72π≈76.2832≈1.11Hz
The frequency at which the object will remain just in contact with the platform is approximately:
f≈1.11Hz
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 1
7 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 2
4 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED OSCILLATIONS
1 Video
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
An object kept on the platform a horizontal platform executing SHM, up and down with amplitude 80 cm. At what frequency will the object just lose contact with the platform?
View SolutionA horizontal platform moves up and down simple harmonically, the total vertical movement being 10 cm what is the shortest period permissible, if object resting on the platform are to remain in contact with it throughout the motion.? Take g=980cms−2
View Solution
Knowledge Check
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
A(a) at the mean position of the platformB(b) for an amplitude of gω2C(c) for an amplitude of g2ω2D(d) at the highest position of the platformA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
Aat the highest position of the platformBat the mean position of the platformCfor an amplitude of gω2Dfor an amplitude of g2ω2A book is resting on shelf that is undergoing vertical simple harmonic oscillations with an amplitude of 2.5 cm. What is the minimum frequency of oscillation of the shell for which the book will lose contact with the shelf ? (Assume that g=10m/s2)
A20 HzB3.18 HzC125.6 HzD10 Hz
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionA body is vibrating in simple harmonic motion with an amplitude of 0.06 m and frequency of 15 Hz . The velocity and acceleration of body is
View SolutionA man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2πHz. Which of the following statement is correct ?

View SolutionWhat force must man exert on rope to keep platform in equilibrium : (Take g=10m/s2)
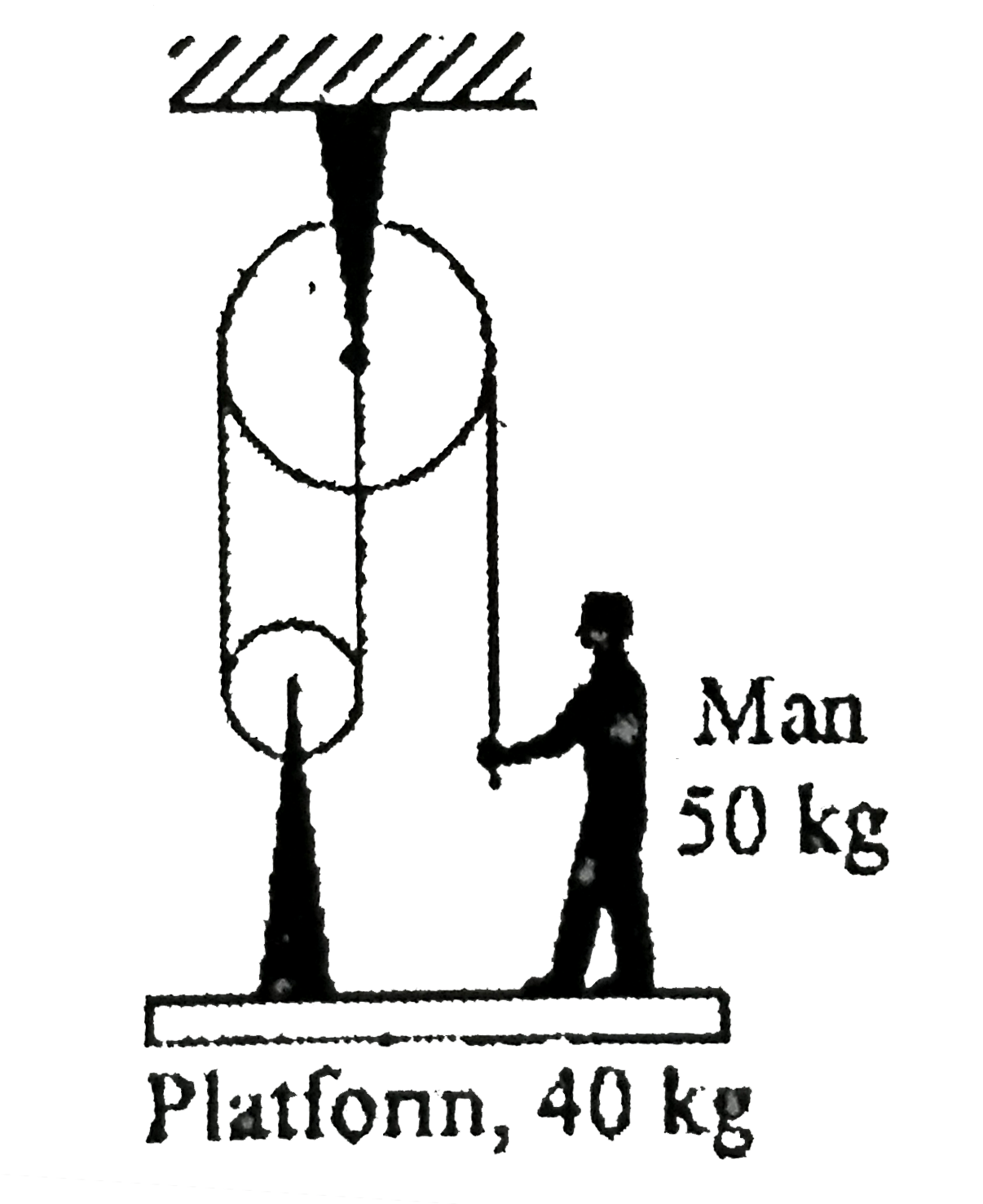
View Solution
