The end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
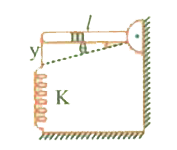
τres=−(Ky)l=−(Klθ)l=−Kl2θ
or −Iω2θ=−Kl2θ
or, −(13ml2)θ(ω)2=−Kl2θ
⇒ ω=√3Km
∴ T=2π√m3K
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 1
7 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 2
4 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED OSCILLATIONS
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
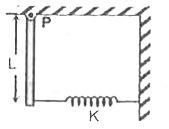
A straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View SolutionTwo identical thin circular, metal plates are at a small separation d. They are connected by a thin conducting rod (AB) of length d. Each plate has area A. An ideal spring of stiffness k is connected to a rigid support and midpoint of rod AB as shown in the figure. Spring is made of insulating material. The system is on a smooth horizontal surface. The entire region has a uniform vertical upward magnetic field B.
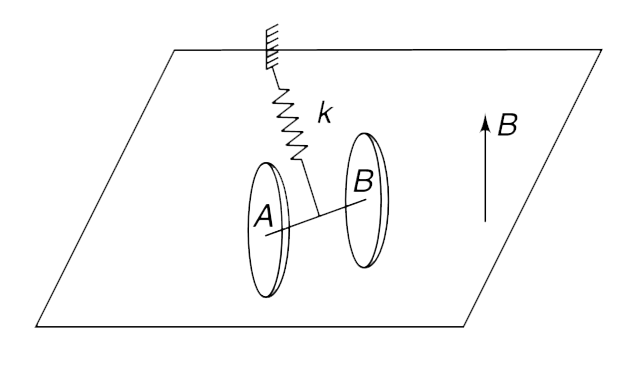
The discs are pulled away from the support and released. Find time period of oscillations. Mass of the two disc plus rod system is M. Neglect any eddy current.
View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be
 Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]
Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]The arrangement shown of a uniform rod of length l and mass m, pivoted at the centre and its two ends attached to two springs of spring constant K1 and K2 . The other end of springs are fixed to two rigid supports the rod which is free to rotate in the horizontal plane , is pushed by a small angle in one direction and released . Teh frequency of oscillation of the rod is
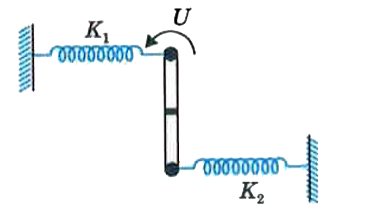 A12π√K1+K2mB12π√K1+K23mC12√3π√K1+K2mD√32π√K1+K2m
A12π√K1+K2mB12π√K1+K23mC12√3π√K1+K2mD√32π√K1+K2m
A particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View SolutionOn compressing a spring by 0.5 m, a restoring force of 20 N is developed. When a body of mass 5 kg is placed on the spring, then calculate the (a) force constant of the spring.
(b) the distance through which the spring is depressed under the weight of the body.
(c ) the period of oscillation of the spring if the the body is pushed down and then released.
View SolutionA particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
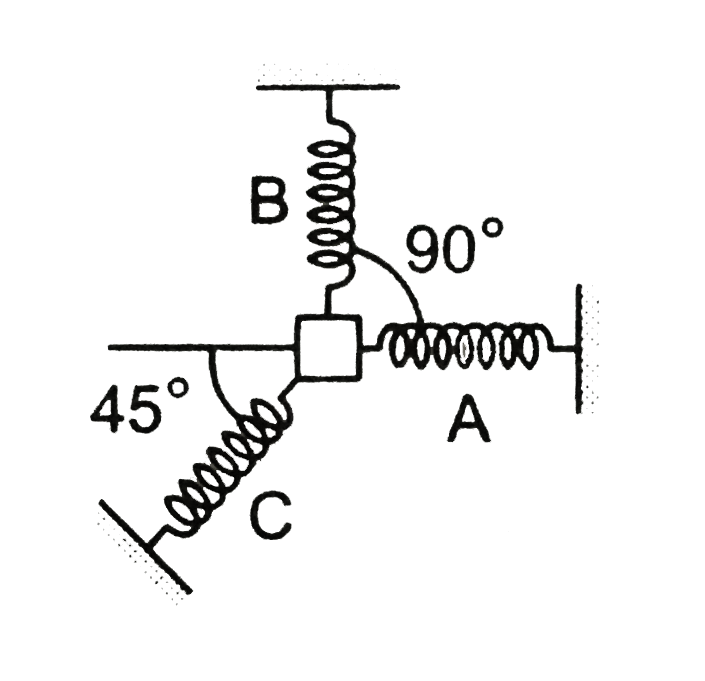
View SolutionA rod of mass m can move vertically on two fixed inclined rod in vertical plane, weight of the rod is blanced by thin liquid film between rods as shown. (Surface tension of liquid is S).
If rod is displaced a little in downward direction and released, then what will be the time period of oscillation of rod.

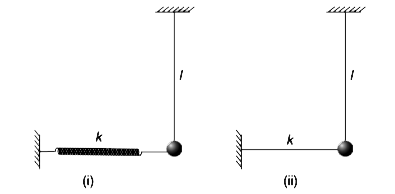
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View Solution
