A particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
T
T
T
T
To solve the problem of finding the time taken for a particle undergoing simple harmonic motion (SHM) to complete 38 of an oscillation, we can follow these steps:
Step 1: Understand the Time Period of SHM
The time period T is the time taken to complete one full oscillation.
Step 2: Determine the Time for 38 of an Oscillation
To find the time taken for 38 of an oscillation, we can express this in terms of the time period T:
Time for 38 oscillation=38×T
Step 3: Calculate the Time Taken in 38 Oscillation
Now, we can calculate the time taken:
Time taken=38T
Step 4: Conclusion
Thus, the time taken for the particle to complete 38 of an oscillation is:
38T
Final Answer
The time taken in 38 oscillation is 38T.
---
The time period T is the time taken to complete one full oscillation.
To find the time taken for 38 of an oscillation, we can express this in terms of the time period T:
Time for 38 oscillation=38×T
Now, we can calculate the time taken:
Time taken=38T
Thus, the time taken for the particle to complete 38 of an oscillation is:
38T
The time taken in 38 oscillation is 38T.
Similar Questions
A particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle performs simple harmonic motion with a period of 2 second. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is 1as.
The value of 'a' to the nearest integer is___________ .
View Solution
Knowledge Check
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A particle is executing simple harmonic motion with a time period T. At time t=0, it is at its position of equilibium. The kinetice energy -time graph of the particle will look like
A B
B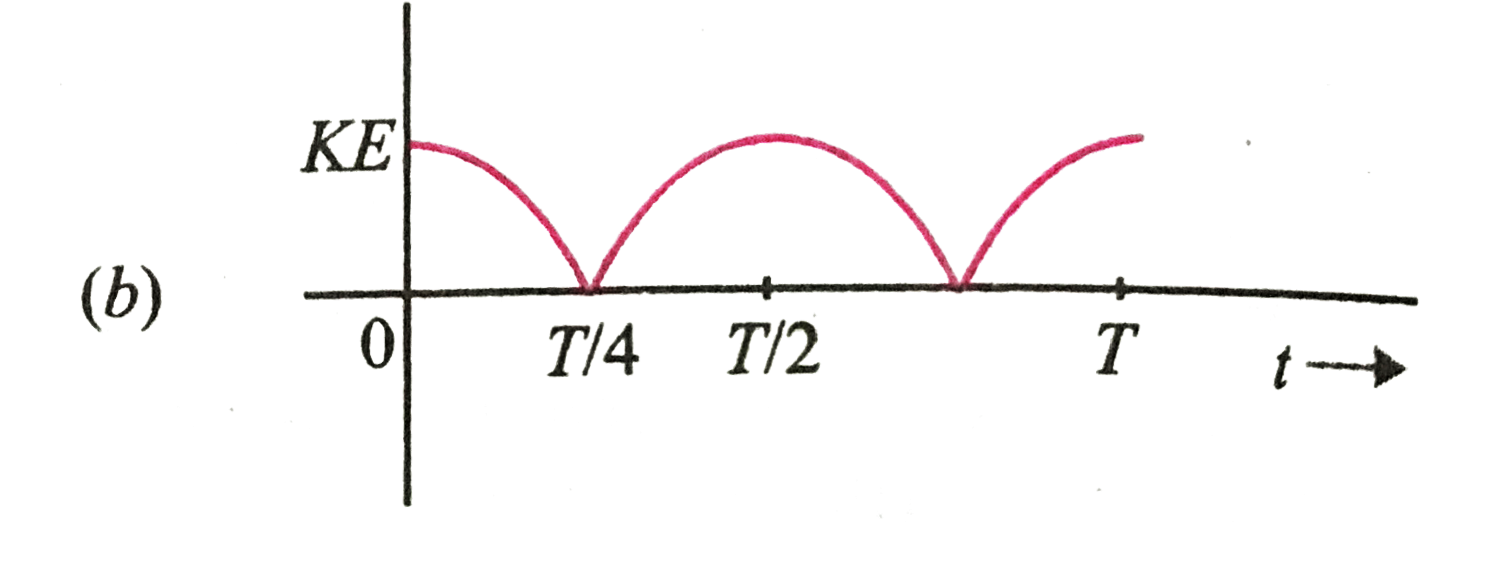 C
C D
D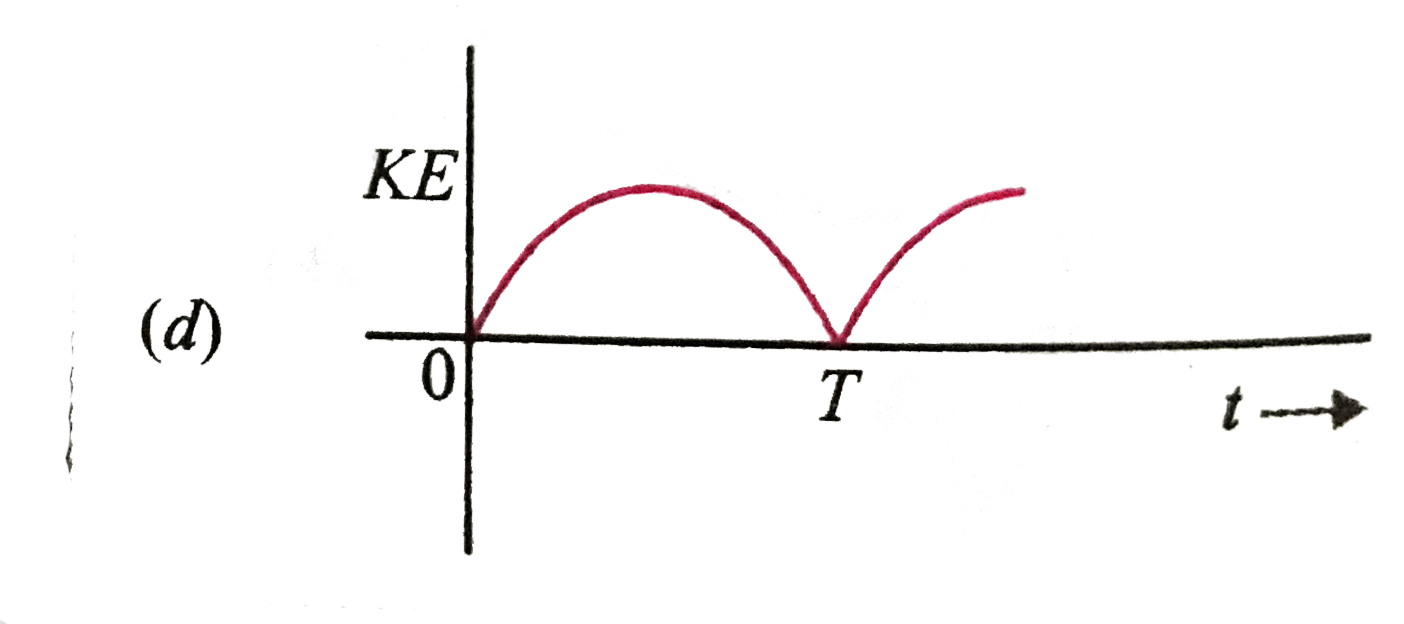
A particle executing a simple harmonic motion has a period of 6 s. The time taken by the particle to move from the mean position to half the amplitude, starting from the mean position is
A14sB34sC12sD32s
A particle executes simple harmonic motion with a time period of 16s. At time t=4s its velocity is 4ms−1. Find its amplitute of motion.
View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionA particle performing simple harmonic motion having time period 3 s is in phase with another particle which also undergoes simple harmonic motion at t=0. The time period of second particle is T (less that 3s). If they are again in the same phase for the third time after 45 s, then the value of T will be
View SolutionThe periodic time of a particle doing simple harmonic motion is 4 second . The time taken by it to go from its mean position to half the maximum displacement (amplitude) is
View SolutionA particle performs simple harmonic motion about O with amplitude A and time period T. The magnitude of its acceleration at t=T8s after the particle reaches the extreme position would be
View Solution