A mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
f
2f
The correct Answer is:A
To solve the problem step by step, we will use the formula for the frequency of oscillation of a mass-spring system and analyze how cutting the spring affects the spring constant.
1. Understand the Frequency Formula:
The frequency of oscillation (f) of a mass (m) attached to a spring with spring constant (k) is given by the formula:
f=12π√km
2. Initial Frequency:
Let the initial frequency of oscillation when the mass is suspended from the original spring (with spring constant k) be:
f=12π√km
3. Effect of Cutting the Spring:
When the spring is cut into two halves, each half will have a new spring constant. The spring constant of a spring is inversely proportional to its length. When the length of the spring is halved, the spring constant doubles. Therefore, the spring constant of one half (let's call it k′) becomes:
k′=2k
4. New Frequency with Half Spring:
Now, if the same mass (m) is suspended from one half of the spring, the new frequency f′ can be calculated using the new spring constant k′:
f′=12π√k′m=12π√2km
5. Relate New Frequency to Old Frequency:
We can relate the new frequency f′ to the original frequency f:
f′=12π√2km=√2⋅12π√km=√2⋅f
6. Final Result:
Therefore, the frequency of oscillation when the mass is suspended from one half of the spring is:
f′=√2⋅f
Conclusion:
The frequency of oscillation of the mass when suspended from one piece of the cut spring is √2 times the original frequency f.
The frequency of oscillation (f) of a mass (m) attached to a spring with spring constant (k) is given by the formula:
f=12π√km
Let the initial frequency of oscillation when the mass is suspended from the original spring (with spring constant k) be:
f=12π√km
When the spring is cut into two halves, each half will have a new spring constant. The spring constant of a spring is inversely proportional to its length. When the length of the spring is halved, the spring constant doubles. Therefore, the spring constant of one half (let's call it k′) becomes:
k′=2k
Now, if the same mass (m) is suspended from one half of the spring, the new frequency f′ can be calculated using the new spring constant k′:
f′=12π√k′m=12π√2km
We can relate the new frequency f′ to the original frequency f:
f′=12π√2km=√2⋅12π√km=√2⋅f
Therefore, the frequency of oscillation when the mass is suspended from one half of the spring is:
f′=√2⋅f
The frequency of oscillation of the mass when suspended from one piece of the cut spring is √2 times the original frequency f.
Similar Questions
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
View SolutionA mass m is suspended from a spring of length l and force constant K . The frequency of vibration of the mass is f1. The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is f2 . Which of the following relations between the frequencies is correct
View Solution
Knowledge Check
A spring has a certain mass suspended from it and its period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is now
AT2BT√2C√2TD2TA spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now T2. The ratio of T2/T1 is
A1/2B1/√2C√2D2A spring has a force constant k and a mass m is suspended from it the spring is cut in two equal halves and the same mass is suspended from one of the halves. If the frequency of oscillation in the first case is n, then the frequency in the second case will be
A2 nBn/√2CnD√2n
The time period of a mass suspended from a spring is T if the spring is cut in to equal part and the same mass is suspended from one of the pert then the time period will be
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
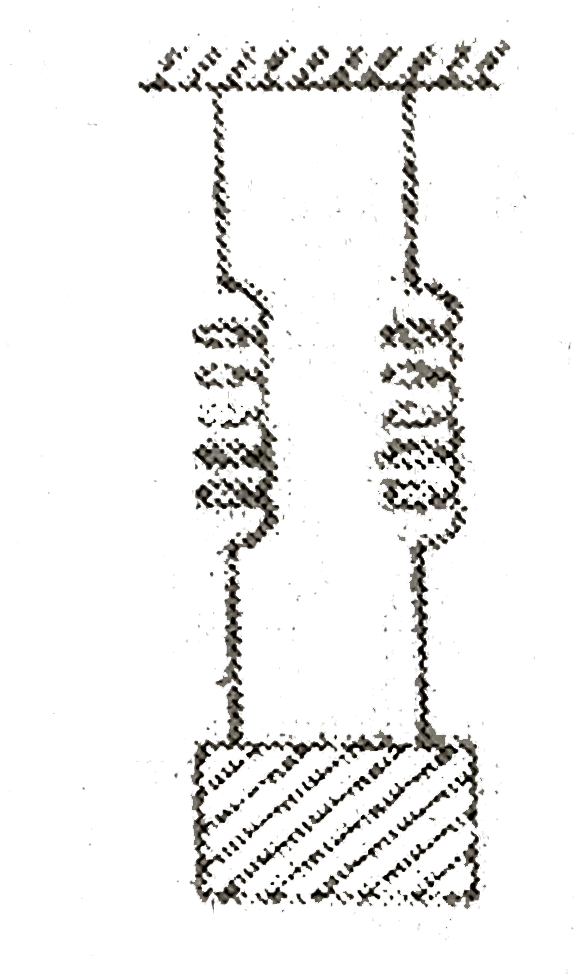
View SolutionThe time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be:
View SolutionA massless spring, having force constant k, oscillates with frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from one half. The frequency of oscillation will now be
View SolutionA spring of force constant k is cut into two equal parts, and mass 'm' is suspended from parallel combination of the springs. Then frequency of small osciollations is
View Solution
