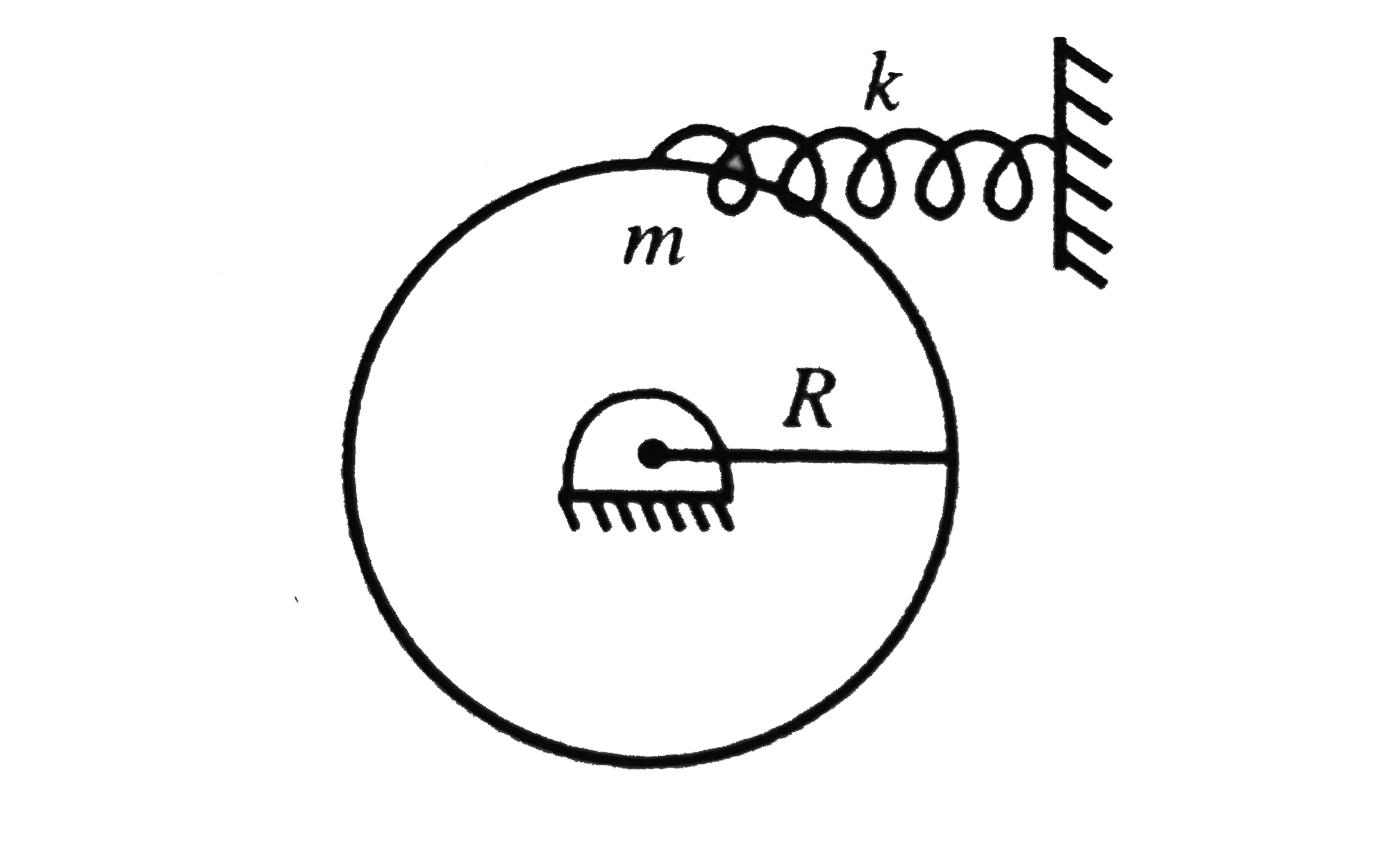
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
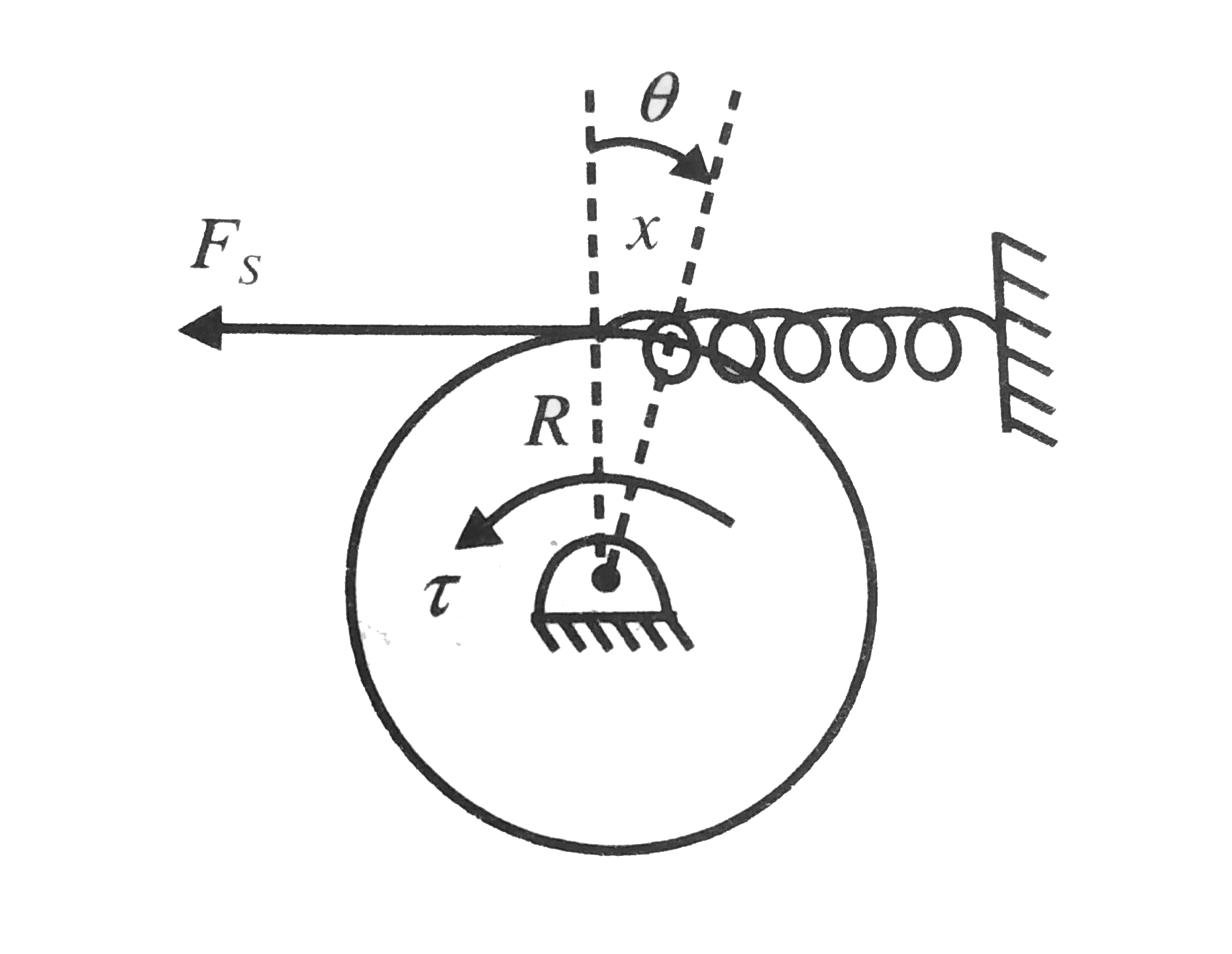
If we twist (rotate) the disc through small clockwise anghe θ, the spring will be deformed (compressed) by a distant x=Rθ, hence the spring force FS=kx=k(Rθ) will produce a restoring torque.
Restoring torque: τ=−FSR where FS=kRθ
This gives τ=−kR2θ
It means after removing the external (applied) torque the restoring torque rotates the disc with an angular acceleration α which will bering the spring-disc system back to its original state.
Newton's law of rotation (or torque equation): Applying Newton's second law of rotation we have.
τ=ICα
where τ==kR2θ
This gives α=−kR2θIC where IC=mR22
Then a=−2kmθ
Comparing the above equation with α=−ω2θ, we have
ω=√2km
After sustituting the values we get ω=2rads.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective type
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Comprehension
Explore 33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
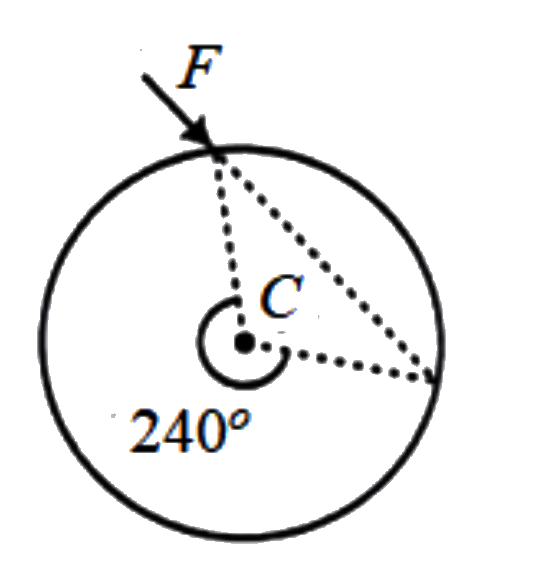
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
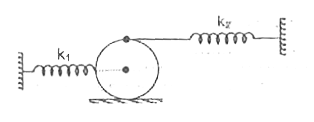
View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View Solution
Knowledge Check
A disc of mass M = 4 kg, radius R = 1 m is attached with two blocks A and B of masses 1 kg and 2 kg respectively on rim and is resting on a horizontal surface as shown in the figure. Find angular frequency of small oscillation of arrangement:
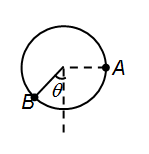 A2.2sec−1B1.42sec−1C1.62sec−1D1.82sec−1
A2.2sec−1B1.42sec−1C1.62sec−1D1.82sec−1A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
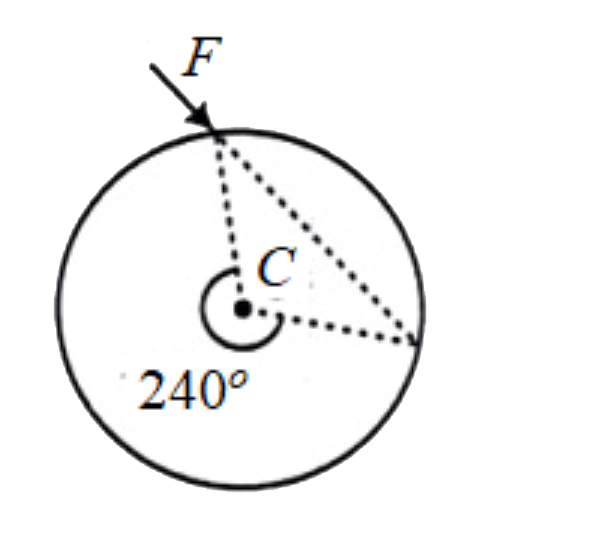 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA uniform cylinder of mass m and radius R is in equilibrium on an inclined plane by the action of a light spring of stiffness k, gravity and reaction force acting on it. If the angle of inclination of the plane is ϕ, then angular frequency of small oscillations of the cylinder is...........
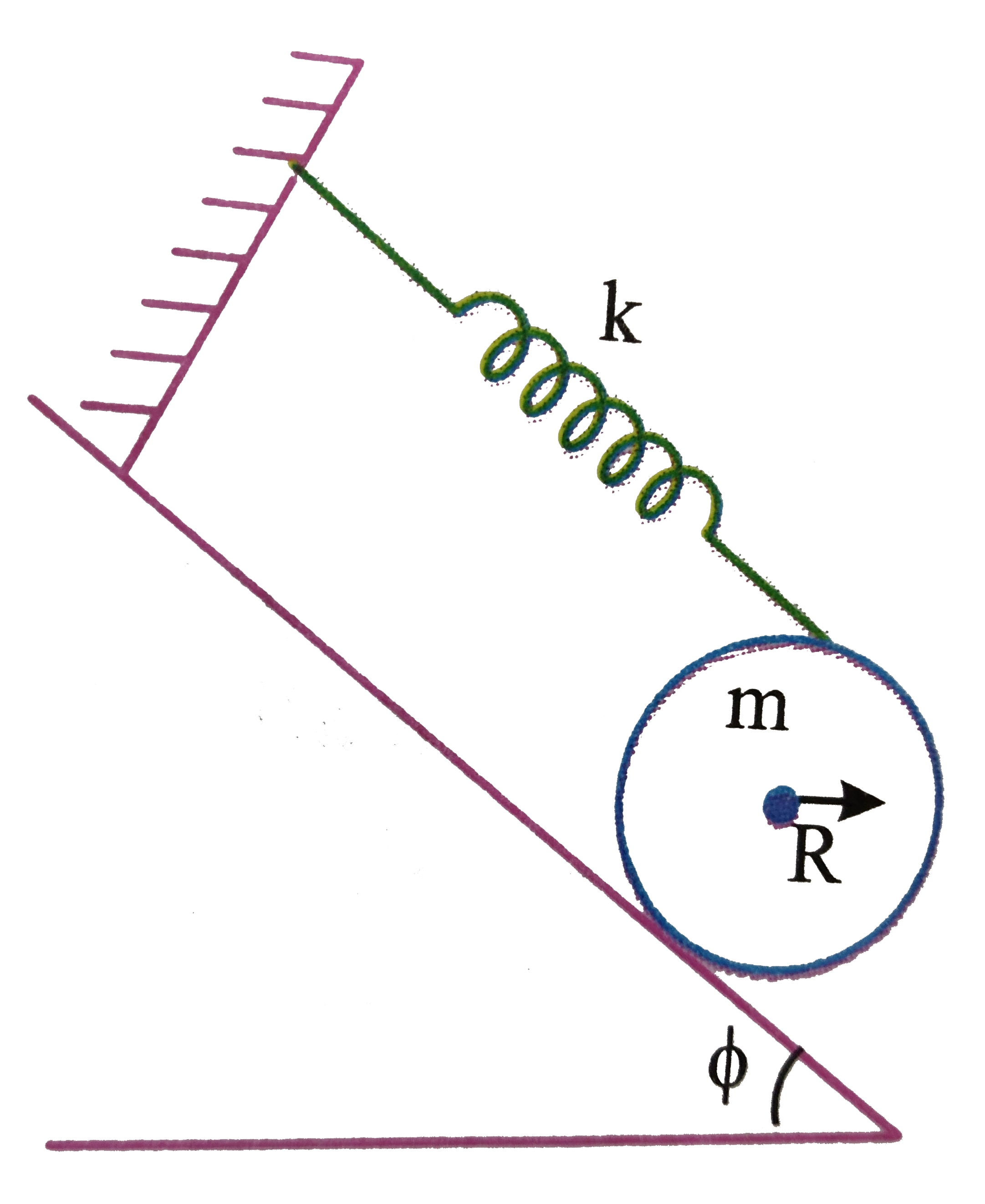 A2√kmB2√2kmC2√2k3mD√2km
A2√kmB2√2kmC2√2k3mD√2km

A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionA uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
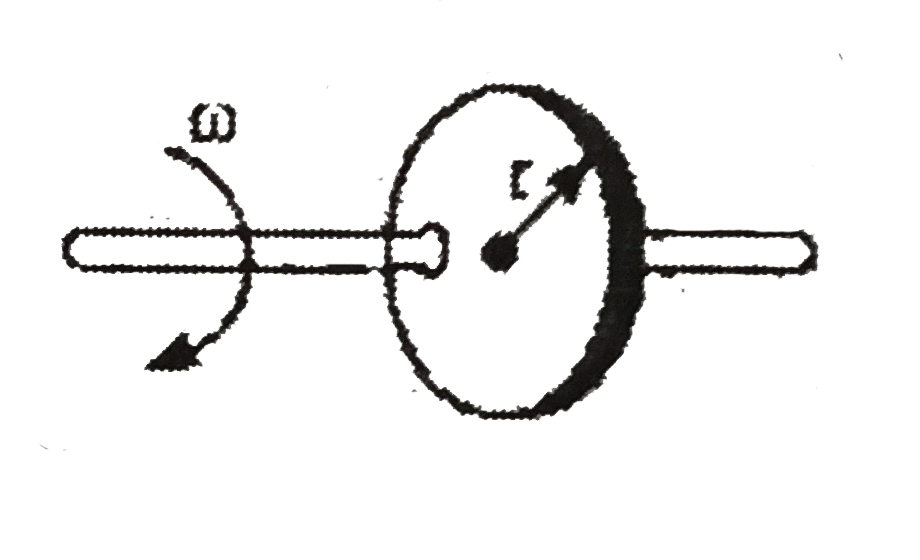
View Solution

