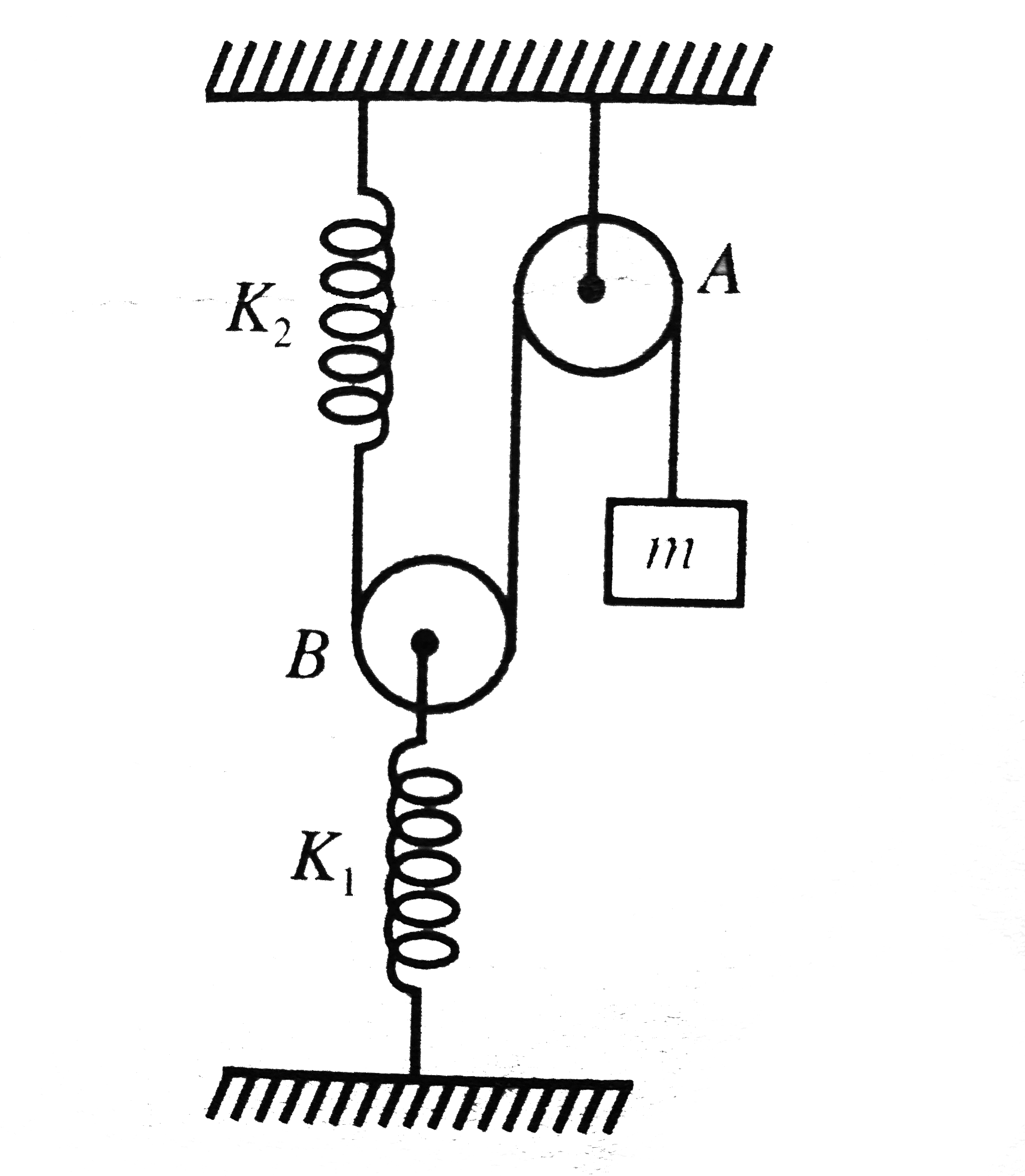
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)

(1) Net sunstituting in the tension in string connecting the block will provide acceleration to the block. We can write
△T=ma .(i)
When the block m is displaced by a distance x beyond equilibrium position, the addition stretch of springs 1 and 2 are x1 and x2 respectively, we can write
x1=x−x22⇒x=2x1+x2 .(ii)
At △T=k2x2 and 2△T=k1x1 then 2(k2x2)=k1x1
⇒x1=2k2x2k1 .(iii)
from eqs. (ii) and (iii) x=2[2k2x2k1]+x2=(4k2+k1)k1x2
⇒x2=k1x(k1+4k2)
and →a=−k1k2(k1+4k2)m.xi ⇒→a=−k1k2(k1+4k2)m.x
ω2==k1k2(k1+4k2)m
Hence R=8023π2m
After substituting the values, we get T=1s
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective type
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Comprehension
Explore 33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
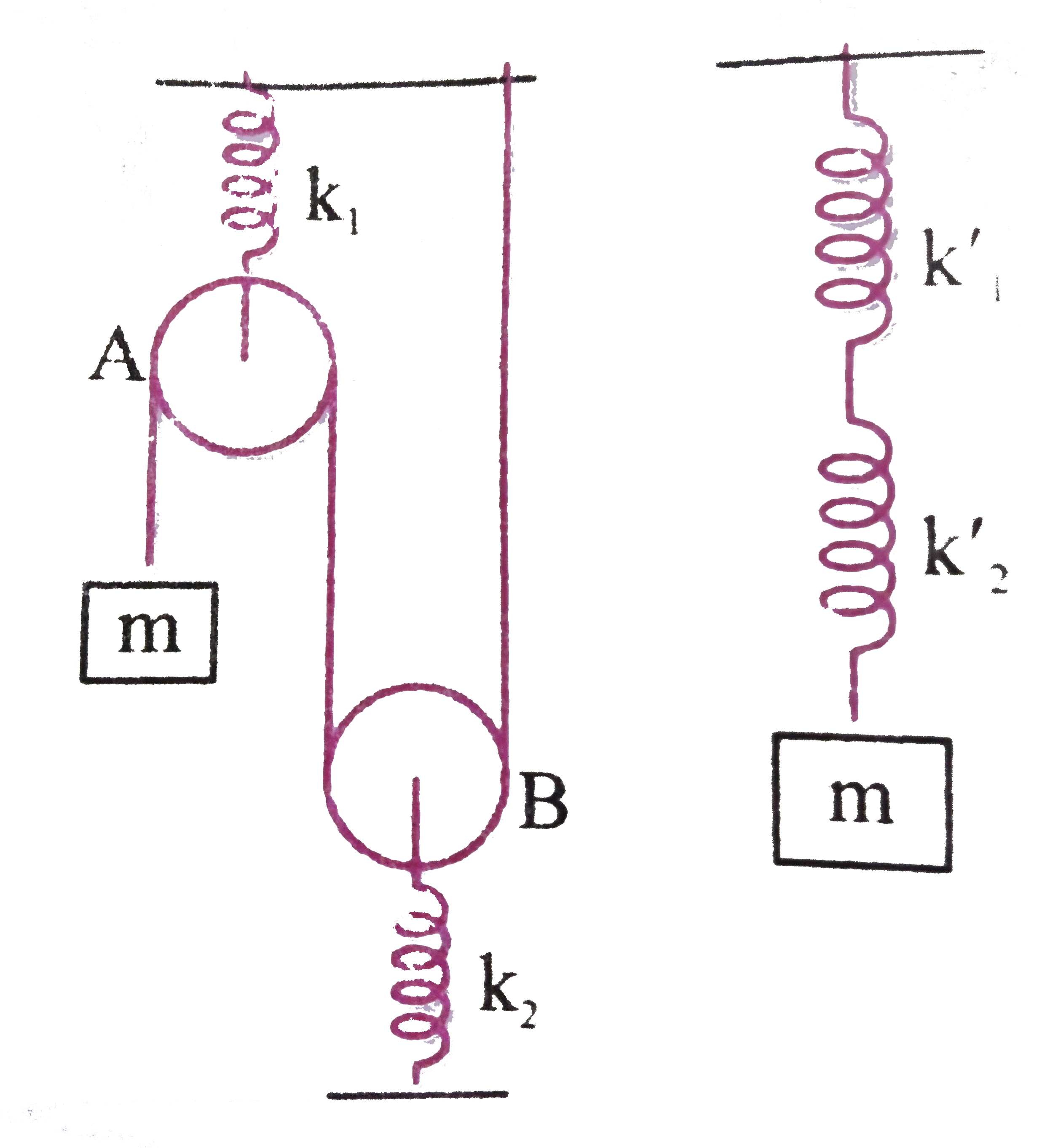
A block of mass m is attached to one end of a light intextensible string passing over a smooth light pulled A and under another smooth light pulled B as shown in Fig. The other end of a springs is fixed to a ceiling. A and B are held by spring of force constant k1 and k2. Find the period of small oscillations of system.
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution
Knowledge Check
A load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
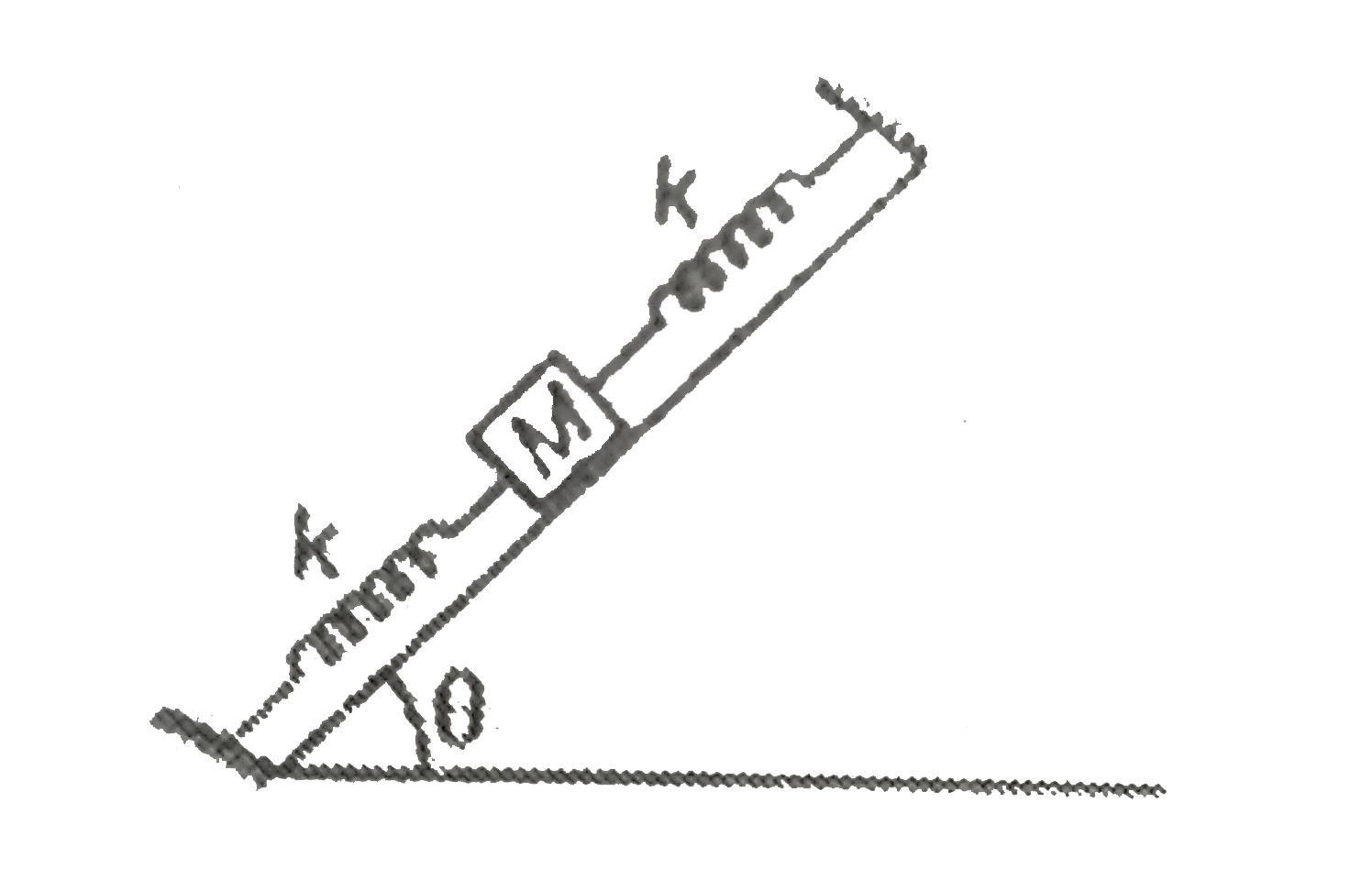
A2π3√10MKB4π√M3KC4π√MKD2π√M3KOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A2π(m2K)1/2B2π(2MK)1/2C2πMgsinθ2KD2π(2MgK)1/2
A2π(m2K)1/2B2π(2MK)1/2C2πMgsinθ2KD2π(2MgK)1/2An object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
AA√k/mBA2k/mCA√m/kDAm/k
A block of mass m is attached to one end of a light inextensible string passing over a smooth light pulley B and under another smooth light pulley A as shown in the figure. The other end of the string is fixed to a ceiling. A and B are held by spring of spring constants k1 and k2. Find angular frequency of small oscillations of small oscillations of the system.

View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View SolutionA massless rod rigidly fixed at O. A sting carrying a mass m at one end is attached to point A on the rod so that OA=a. At another point B(OB=b) of the rod, a horizontal spring of force constant k is attached as shown. Find the period of small vertical oscillations of mass m around its euqilibrium position.
_E01_116_Q01.png)
View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View Solution

