
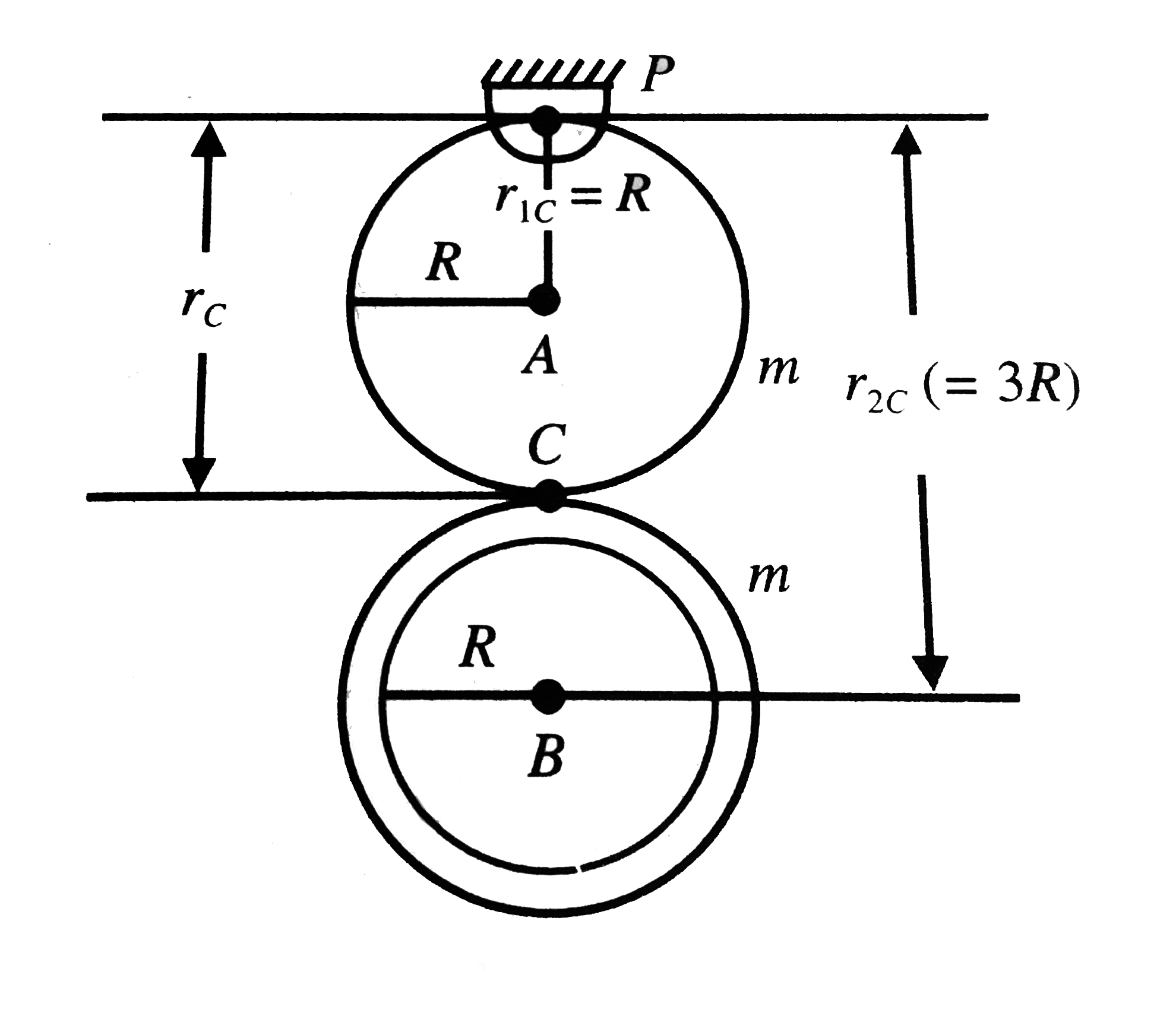
A uniform disc of mass m and radius R=8023π2m is pivoted smoothly at P. If a uniform disc of mass m and radius R is welded at the lowest point of the disc, find the period of SHM of the system (disc + ring). (in seconds)
The time period of a physical pendulum is
T=2π√IPMgr
Here we have three quantities IP, m and r
Let us calculate the quentities one by one as follows: Finding IP:IP=(IP)disc+(IP)ring
Where (IP)disc=IA+m(PA)2=mR22+mR2=3mR22
and (IP)ring=Ib(PB)2=mR2+m(3R)=10mR2
Then, we have IP=32mR2=10mR2=232mR2
Finding r.
r=→rC=m1→r1+m2+→r2Cm1+m2
where m1=m,m2=m
→r1C=−R and r2C=−3R
This gives rC=2R
Finding M:
M=(m)disc+(m)ring=m+m=2m
Substituting IP=232mR2,M=2m and r=2R in the expression
T=2π√IPMgr we have T=π√23Rg
After subsituting the value we get t=2s.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
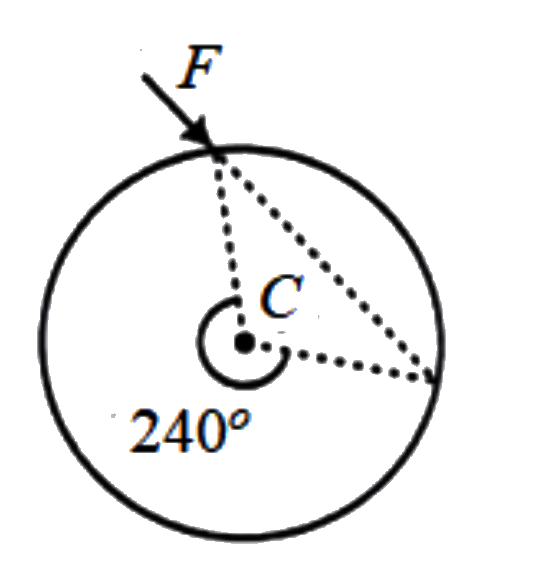
View Solution
Knowledge Check
The M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
A12MR2B14MR2CMR2D34MR2The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
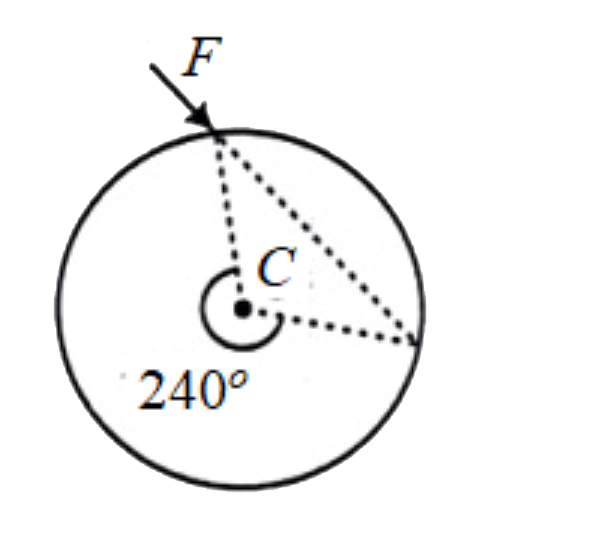
View SolutionA force F acts tangentially on a part of a uniform disc of mass 'm' and radius 'R' hinged at point O. The force exerted by hinge on the portion of disc initially.

View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution
