A particles starts from point x=−√32A and move towards negative extrene as shown . If the time period of oscillation is T , them

The equation of the SHM is x=Asin(2πT+4π3)
The time taken by the particle tto go directly from its initial position to negative extreme is T12
The time taken by the particle to reach at mean position is T3
The equation of the SHM is x=Asin(2πT+π3)
The correct Answer is:A, B, C
Step by step video, text & image solution for A particles starts from point x=-sqrt(3)/(2) A and move towards negative extrene as shown . If the time period of oscillation is T , them by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective type
Explore 3 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective type
Explore 2 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A particle starts from point x=−√32A and move towards negative extreme as shown
(a) Find the equation of the SHM.
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
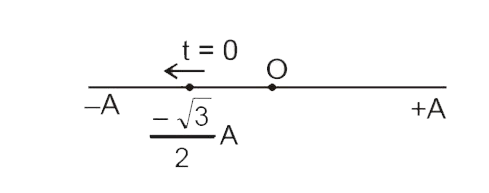
View SolutionA particle starts from point x=−√32A and move towards negative extreme as shown,
_S01_011_Q01.png)
(a) Find the equation of the SHM
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
View Solution
Knowledge Check
A particle moves such that acceleration is given by a=−4x. The period of oscillation is
AπB2πC1πD2πA particle starts from a point P at a distance of A/2 from the mean position O& travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of motion of particle is :
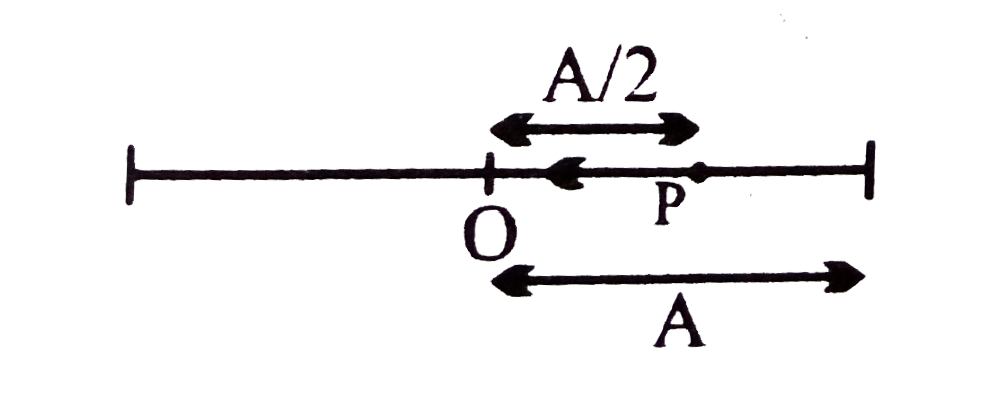 AX=Asin(2πTt+π6)BX=Asin(2πTt+5π6)CX=Acos(2πTt+π6)DX=Acos(2πTt+π3)
AX=Asin(2πTt+π6)BX=Asin(2πTt+5π6)CX=Acos(2πTt+π6)DX=Acos(2πTt+π3)A particle starts from a point P at a distance of A/2 from the mean position O and travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of the motion of particle is
 Ax=Asin(2πTt+π6)Bx=Asin(2πTt+5π6)Cx=Acos(2πTt+π6)Dx=Acos(2πTt+π3)
Ax=Asin(2πTt+π6)Bx=Asin(2πTt+5π6)Cx=Acos(2πTt+π6)Dx=Acos(2πTt+π3)
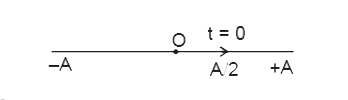
A particle starts from A/2 and moves towards positive extreme as shown below. Find the equation of the SHM. Given amplitude of SHM is A.
View SolutionA particle moves so that its acceleration a is give by a=bn where x is displacement from equilibrium position and b is non negative real constant the time period of oscillation of the particle is
View SolutionA particle moves so that its acceleration a is give by a=bn where x is displacement from equilibrium position and b is non negative real constant the time period of oscillation of the particle is
View SolutionA particle starts from origin and moving along x−axis. Whose v−t graph is as shown . Choose the INCORRECT statement :
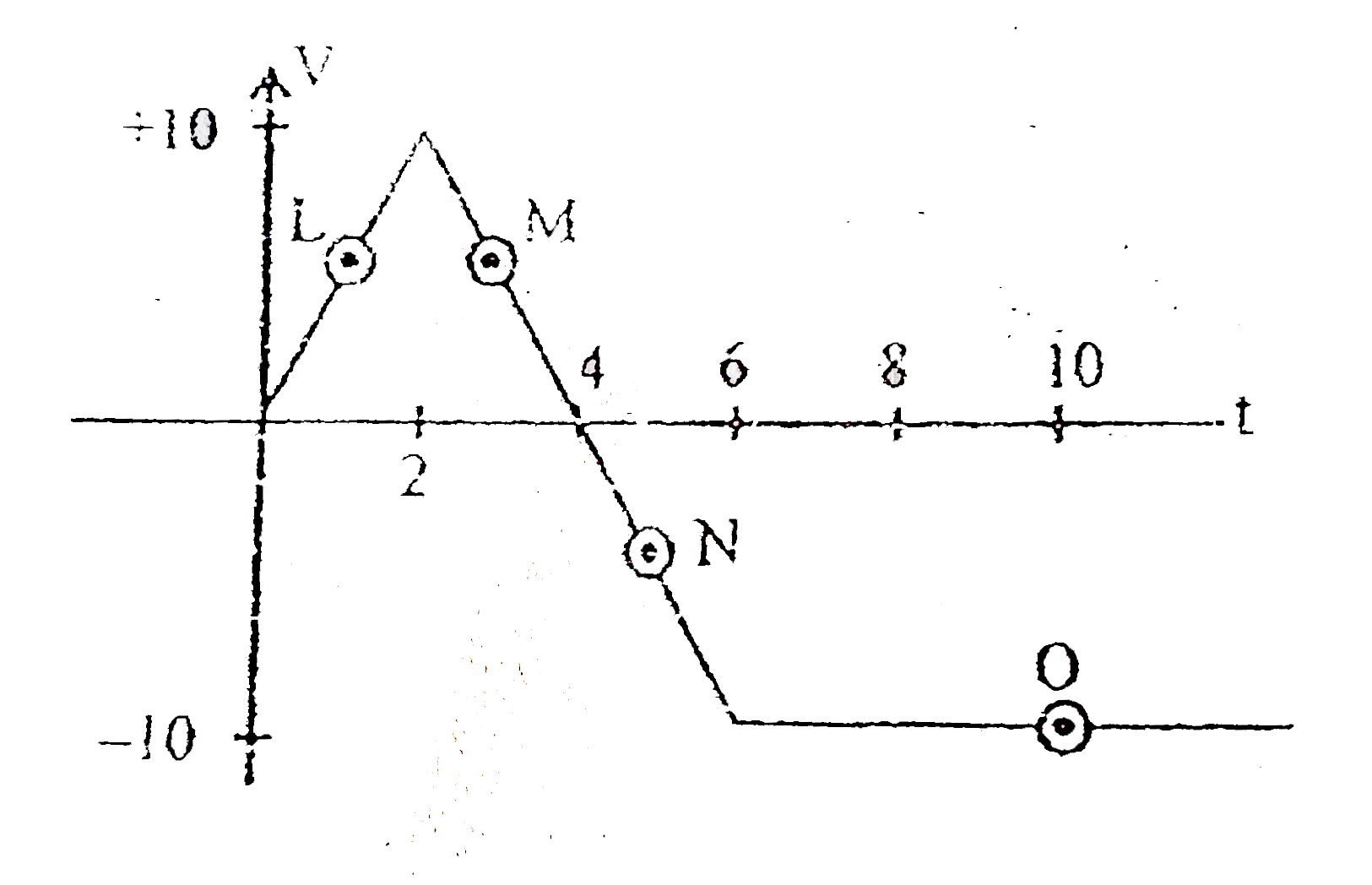 .
.
View SolutionA particle starts from rest x = - 2.25 m and moves along the x - axis with the v - t graph as shown. The time when the particle crosses the origin is :
View Solution

