A particle starts from A/2 and moves towards positive extreme as shown below. Find the equation of the SHM. Given amplitude of SHM is A.
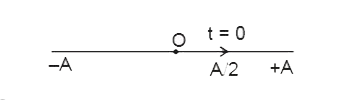
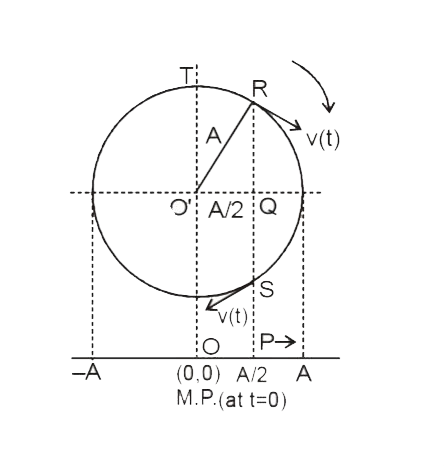
We will solve the above problem with the help of horizontal phasor.
Step 1. Draw a perpendicular line in upward direction from point P on the circle which cuts it at point R & S
Step 2. Horizontal compoment of v(t) at R gives the direction P to A while at S gives P to O. So at t = 0 particle is at R
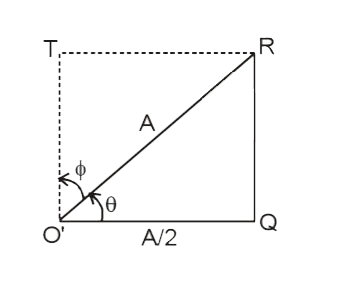
Step 3. In Δ ORQ
cos θ=A/2A=60∘⇒ϕ=30∘
So equation of the SHM is x = A sin (ωt+30∘)
Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-A )
Explore 8 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
A particle starts from mean position and moves towards positive extreme as show below. Find the equation of the SHM, Amplitude of SHM is A.
_S01_003_Q01.png)
View SolutionA particle start form mean position and moves towards positive extreme as shown. Find the equation of the SHM. Amplitude of SHM is A.

View Solution
Knowledge Check
If the particle in linear S.H.M. starts from the extreme left position, then its equation of motion is given by
Ax=Asin(ωt+π/2)Bx=Asin(ωt−π/2)Cx=−Asin(ωt+π/2)Dx=AcosωtA particle performing a linear S.H.M. starts from the positive extremity. Then the epoch of the particle is
AZeroBπ radianCπ/2 radianD2π radianWhen a particle executing a linear S.H.M. moves from its extreme position to the mean position, its
AK.E. decreases and potential energy increasesBK.E. increases and potential energy decreasesCpotential energy becomes zero but kinetic energy remains constantDP.E. increases but the K.E. becomes zero
A particle starts from point x=−√32A and move towards negative extreme as shown
(a) Find the equation of the SHM.
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
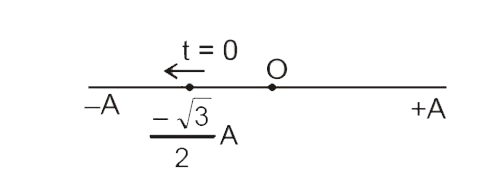
View SolutionA particle starts from point x=−√32A and move towards negative extreme as shown,
_S01_011_Q01.png)
(a) Find the equation of the SHM
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
View SolutionWrite the equation of SHM for the sitution shown below :
_S01_004_Q01.png)
View SolutionTwo particles A and B oscillates in SHM having same amplitude and frequencies fA and fB respectively. At t=0 the particle A is at positive extreme position while the particle B is at a distance half of the amplitude on the positive side of the mean position and is moving away from the mean position.
View SolutionThe periodic time of a particle performing a linear S.H.M. is 12 sec. It starts from the mean position. After 2 seconds, its velocity is found to be πcm/sec. What is the amplitude of S.H.M. ?
View Solution

