A particle start form mean position and moves towards positive extreme as shown. Find the equation of the SHM. Amplitude of SHM is A.

General equation of SHM can be written as x=Asin(ωt+ϕ)
At t=0,x=0
∴0=Asinϕ
∴Φ=0,π,ϕ∈[0,2π)
Also, at t=0,v=+ve
∴Aωcosϕ=+ve
or, ϕ=0
Hence, if the particle is at mean position at t=0 and is moving towards +ve extreme, then the equation of SHM is given by x=Asinωt
Similarly
for ϕ=π
∴ equation of SHM is x=A(ωt+π)
or, x=−Asinωt

Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Solved Miscellaneous Problems
Explore 9 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Board Level Exercise
Explore 24 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
A particle starts from mean position and moves towards positive extreme as show below. Find the equation of the SHM, Amplitude of SHM is A.
_S01_003_Q01.png)
View SolutionA particle starts from A/2 and moves towards positive extreme as shown below. Find the equation of the SHM. Given amplitude of SHM is A.
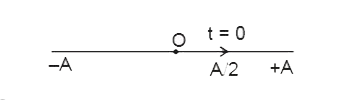
View Solution
Knowledge Check
Particle moves from extreme position to mean position, its
Akinetic energy increases, potential energy decreasesBkinetic energy decreases, potential increasesCboth remains constantDpotential energy becomes zero and kinetic energy remains contantA particle starts from a point P at a distance of A/2 from the mean position O and travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of the motion of particle is
 Ax=Asin(2πTt+π6)Bx=Asin(2πTt+5π6)Cx=Acos(2πTt+π6)Dx=Acos(2πTt+π3)
Ax=Asin(2πTt+π6)Bx=Asin(2πTt+5π6)Cx=Acos(2πTt+π6)Dx=Acos(2πTt+π3)A particle performing a linear S.H.M. starts from the positive extremity. Then the epoch of the particle is
AZeroBπ radianCπ/2 radianD2π radian
A particle starts from point x=−√32A and move towards negative extreme as shown
(a) Find the equation of the SHM.
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
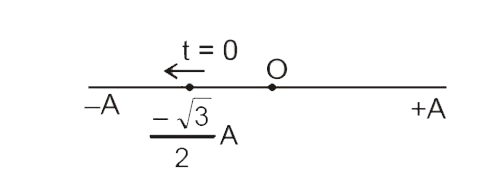
View SolutionA particle starts from point x=−√32A and move towards negative extreme as shown,
_S01_011_Q01.png)
(a) Find the equation of the SHM
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
View SolutionA particle executes SHM from extreme position and covers a distance equal to half to its amplitude in 1 s.
View SolutionA particle starts from a point P at a distance of A/2 from the mean position O& travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of motion of particle is :
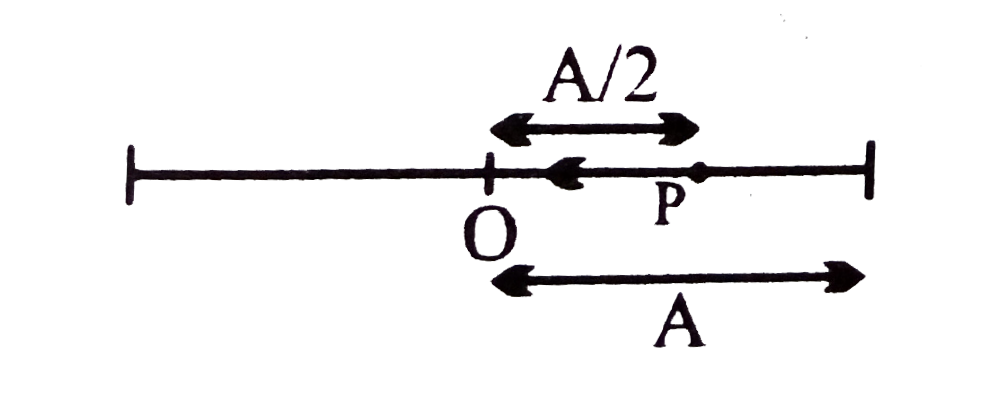
View SolutionA particle performing SHM starts from mean position. The phase of that particle is π/s when it has
View Solution

