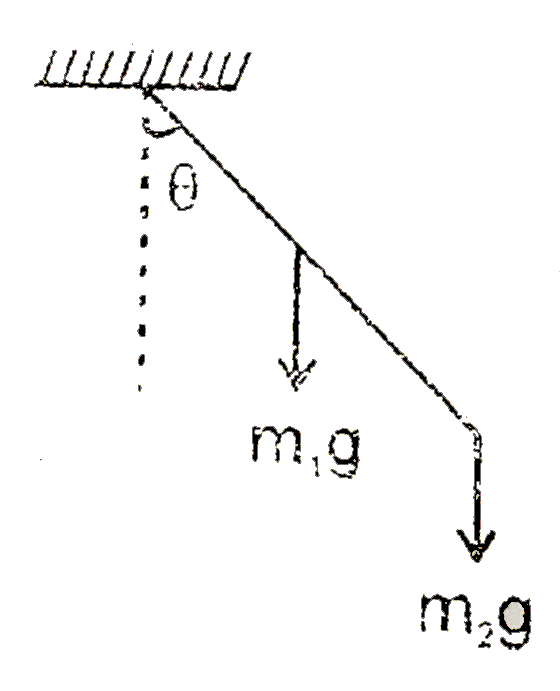
Two point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.

The correct Answer is:1
Net rostoring about O
=m1gl1sinθ+m2gl2sinθ=(m1l1+m2l2)gsinθ
⇒τrestoring=(m1l1+m2l2)gsinθ
compare with τ=Cθ
T=2π√IoC=2π
⎷(m1l21+m2l22)(m1l21+m2)g=1π.
Topper's Solved these Questions
Similar Questions
A compound pendulum consists of a rigid light rod having two spherical bobs of masses m1andm2 at distance l1andl2 from the centre of suspension. Find the time period of oscillations of the pendulum
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
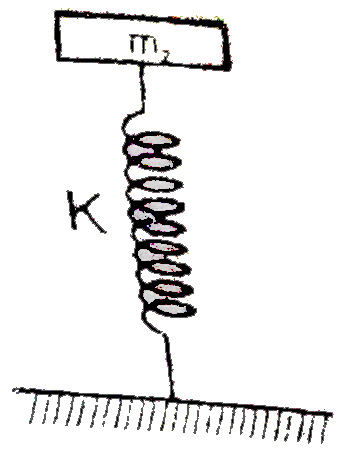
View Solution
Knowledge Check
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)
The system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionTwo masses m1 and m2 are attached to the ends of a light rod of length l.The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is (m1=m and m2 =2m)
View SolutionA wire of length L is hanging from a fixed support. The length changes to L1andL2 when masses M1andM2 are suspended respectively from its free end. Then L is equal to
View SolutionTwo particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
View SolutionTwo particles of masses m1 and m2 are connected with a rigid rod of length l. If a force F acts perpendicular to the rod then (a1&a2 are instantaneous of m1&m2)

View Solution