A compound pendulum consists of a rigid light rod having two spherical bobs of masses m1andm2 at distance l1andl2 from the centre of suspension. Find the time period of oscillations of the pendulum
The correct Answer is:T=2π√m1l12+m2l22m1l1+m2l2
Step by step video, text & image solution for A compound pendulum consists of a rigid light rod having two spherical bobs of masses m_(1) and m_(2) at distance l_(1) and l_(2) from the centre of suspension. Find the time period of oscillations of the pendulum by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE AND COMPOUND PENDULUMBook:NN GHOSHChapter:SIMPLE AND COMPOUND PENDULUMExercise:Exercise
Explore 24 Videos
- SECOND LAW OF THERMODYNAMICSBook:NN GHOSHChapter:SECOND LAW OF THERMODYNAMICSExercise:All Questions
Explore 7 Videos
- SIMPLE HARMONIC MOTIONBook:NN GHOSHChapter:SIMPLE HARMONIC MOTIONExercise:Eexercies
Explore 39 Videos
Similar Questions
Two point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.

View Solution(a) Find the time period of oscillations of a torsinal pendulum, if the torsional, constant of the wire is K=10π2J/rad. The moment of inertia of rigid body is 10kgm2 about the axis of rotation.
(b) A simple pendulum of length l=0.5m is hanging from ceiling of a car. the car is kept on a horizontal plane. The car starts acceleration of 5m/s2. find the time period of oscillations of the pendulum for small amplitudes about the mean position.
View Solution
Knowledge Check
What is the maximum velocity of the bob of a second's pendulum, if the amplitude of oscillation of the pendulum is 0.1 m ?
A0.2 m/sB0.5 m/sC0.3142 m/sD0.6284 m/sThe position of centre of mass of a system consisting of two particles of masses m1 and m2 seperated by a distance L apart , from m1 will be :
Am1Lm1+m2Bm2Lm2+m2Cm2m1LDL2The periodic time of a simple pendulum is 3 sec. The mass of its hollow spherical bob is 100 gram. The bob is then filled with sand, so that the mass of the bob becomes 200 gram. Then the new period of oscillation of the simple pendulum wil be
A6 secB12 secC3 secD9 sec
A simple pendulum of length 'l' and having bob of mass 'm' is doing angular SHM inside water A constant buoyant force equal to half the weight of he bob is acting on the ball. Find the time period of oscillation?
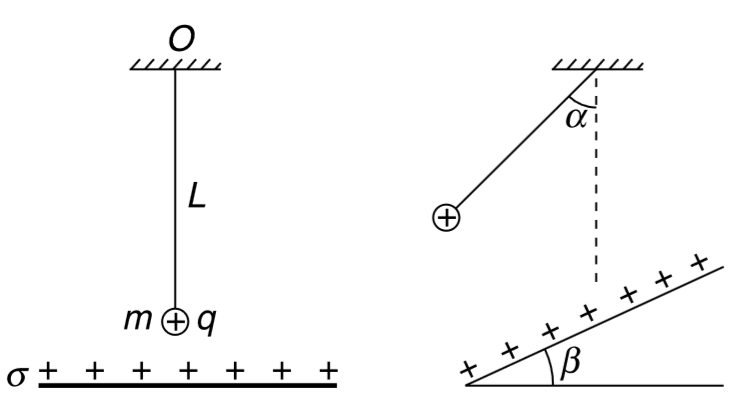
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
View SolutionA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will be
View SolutionA pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
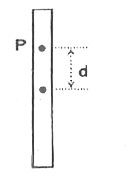
The time period of this pendulum when d = L/2 will be
View Solution

