What would be the period of the free oscillations of the system shown here if mass M1 is pulled down a little force constant of the spring is k, mass of fixed pulley is negligible and movable pulley is smooth
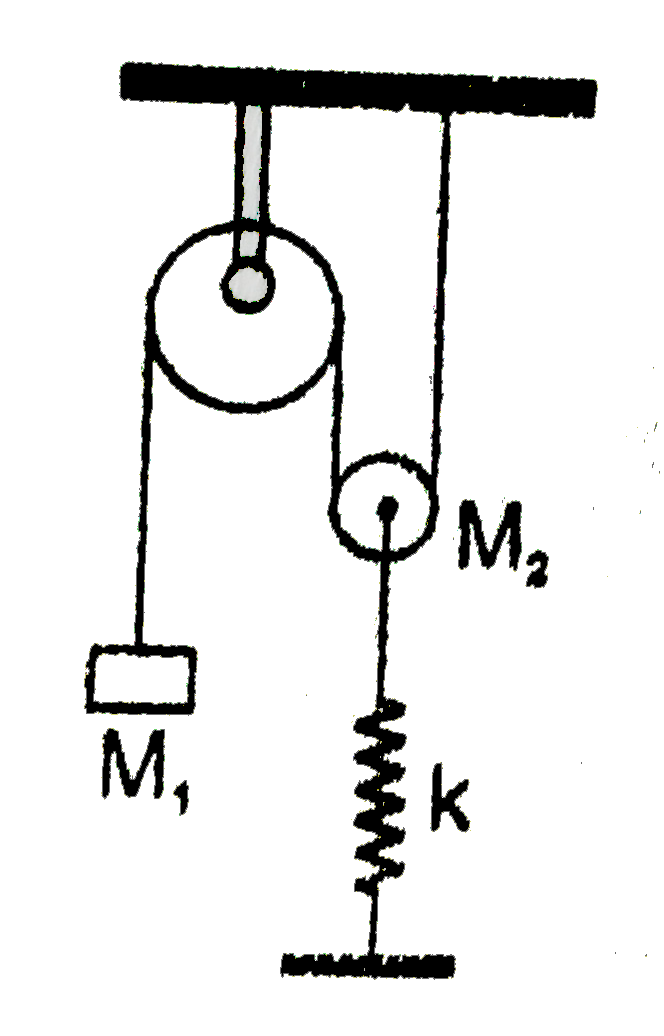
The correct Answer is:T=2π√M2+4M1k

(i) Equilibrium position determination
M1g=T→ (from FBD of M1)
2T=M2g+kx0 (from FBD of M2)
∴2M1g=M2g+kx0
∴kx0=2M1g−M2g
(ii) Displace block M1 by small disp, x by
At new displacement position
−Mgx+12M1V2+12M2(v2)2+M2g(x2)+12K(x0+x2)2x=C
−M1g'dxdt+12M12vdvdt+M282vdvdt+M2g2dxdt+K22(x0+x2)(12dxdt)=0
⇒−M1g+M1a+M2a4+M2g2+K2(x0+x2)=0, (where a=dvdt)
⇒−M1g+M2g2+M1a+M2a4+Kx02+Kx4=0 (from equilibrium −M1g+M2g2+Kx02=0)
Hence, 4M1+M24a=−Kx4
∴a=−K4M1+M2x,ω2=K(4M1+M2)
ω=√K(4M1+M2),T=2πω
∴T2=2π√4M1+M2K
Topper's Solved these Questions
Similar Questions
Knowledge Check
The period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
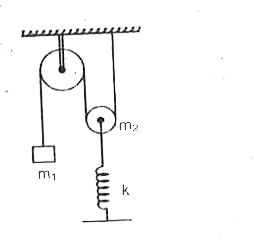 AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2k
AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2kComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
ACLBV1CLCCLDLCFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k
A mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
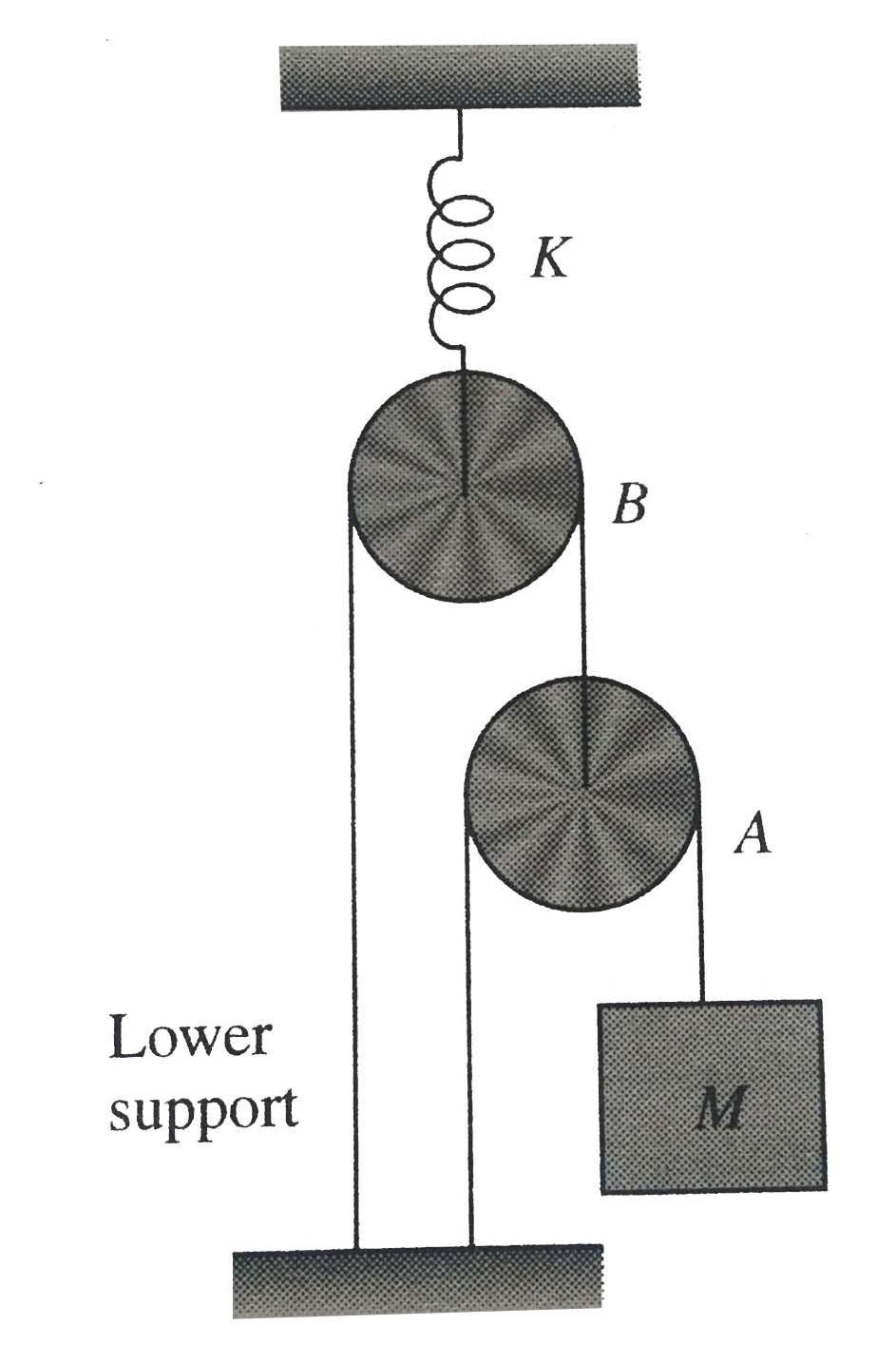
The extension produced in the spring is given by
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.

If each of the pullies A and B has mass M, then find the net tension force acting on the lower support. Asumme pulleys to be frictionaless.
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
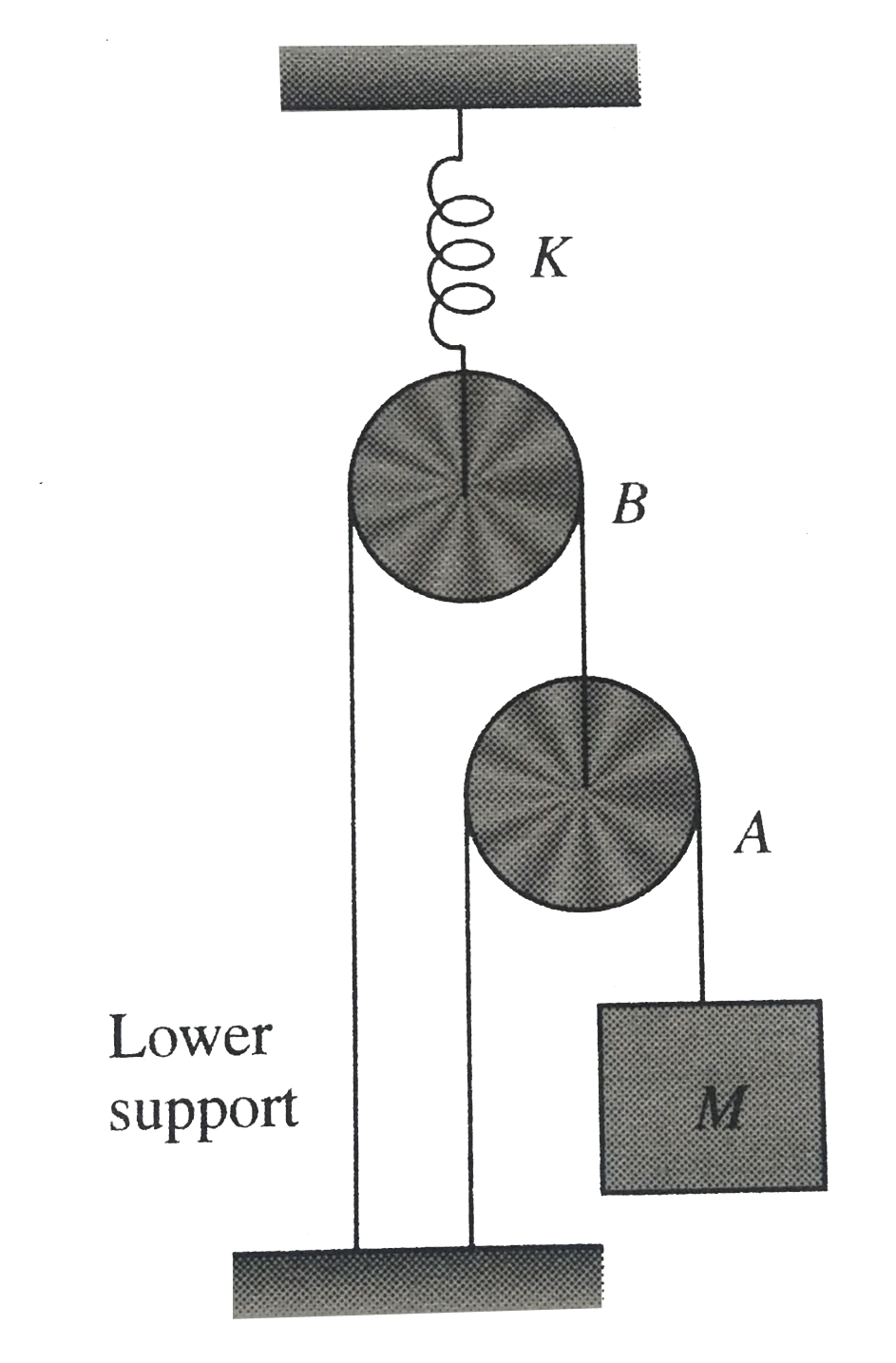
Find the net tension force acting on the lower support.
View SolutionIn the system shown in the figure, which the following is correct? (Pulleys and strings are of negligible mass)
View Solution

