
Two simple pendulums A and B having lengths l and l4 respectively are released from the position as shown in Fig. Calculate the time (in seconds) after which the two strings become parallel for the first time. (Take l=90π2m and g=10ms2.
The correct Answer is:π3√lg
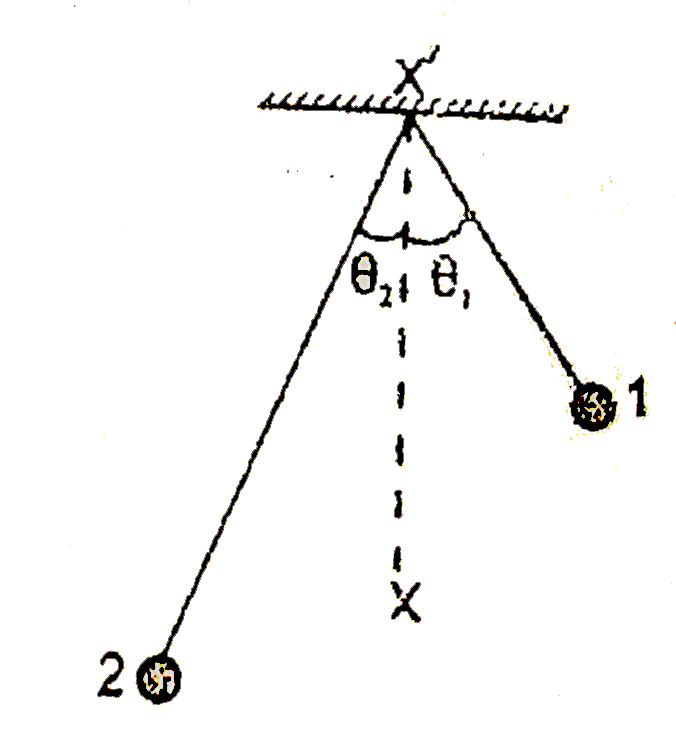
The angular position of pendulum 1 and 2 are (taking angles to the right of reference line ×' to be positive)
θ1=θcos(4πTt), [where T=2π√lg]
θ2=−θcos(2πT)t=cos(2πTt+π)
F for the strings to be parallel for the first time
or cos(4πTt)=cos(2πTt+π) ltbr> ∴4πTt=2nπ±(2πTt+π)
for n=0,t=T2
for n=1,t=T6,3T2
∴ Both the pendulum are parallel to each other for the first time after t=T6=√lg
Topper's Solved these Questions
Similar Questions
Two simple pendulum A and B having lengths l and l/4 respectively are released from the positions as shown in figure. Calculate the time after which the release of the two strings become parallel for the first time. Angle θ is very small.

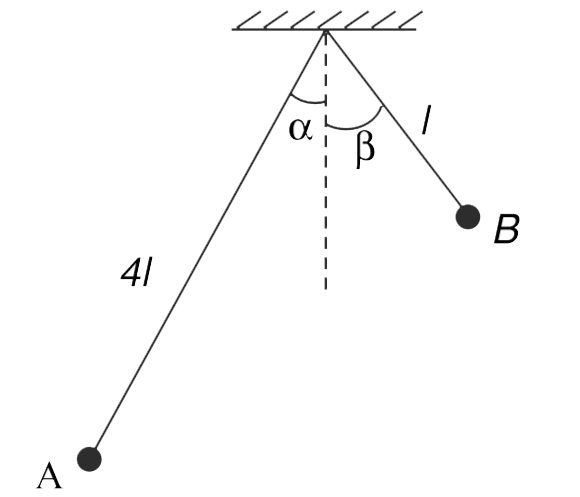
View SolutionTwo simple pendulums A and B have length 4l and l respectively. They are released from rest from the position shown. Both the angles α and β are small. Calculate the time after which the two string become parallel for the first time if-
(a) α=β " " (b)β=1.5α
View Solution
Knowledge Check
Two simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
A8π3√lgBπ3√lgC2sDNone of theseTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
A3:5B4:5C2:5D1:2Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
AL/3B3L/4C4L/3D5L/3
Two simple pendulums of length 1m and 1.21 m are started oscillating from some position. Find the minimum time (in second) after which they again start from same position.
View SolutionTwo simple pendulum have lengths land 25l16 . At t=0 they are in same phase after how may oscillations of smaller pendulum will they be again in phase for first time ?
View SolutionTwo balls are released from the same height at an interval of 2s. When will the separation between the balls be 20m after the first ball is released? Take g=10m/s2.
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution
