
Two simple pendulums and having lengths and respectively are released from the position as shown in Fig. Calculate the time (in seconds) after which the two strings become parallel for the first time. (Take m and .
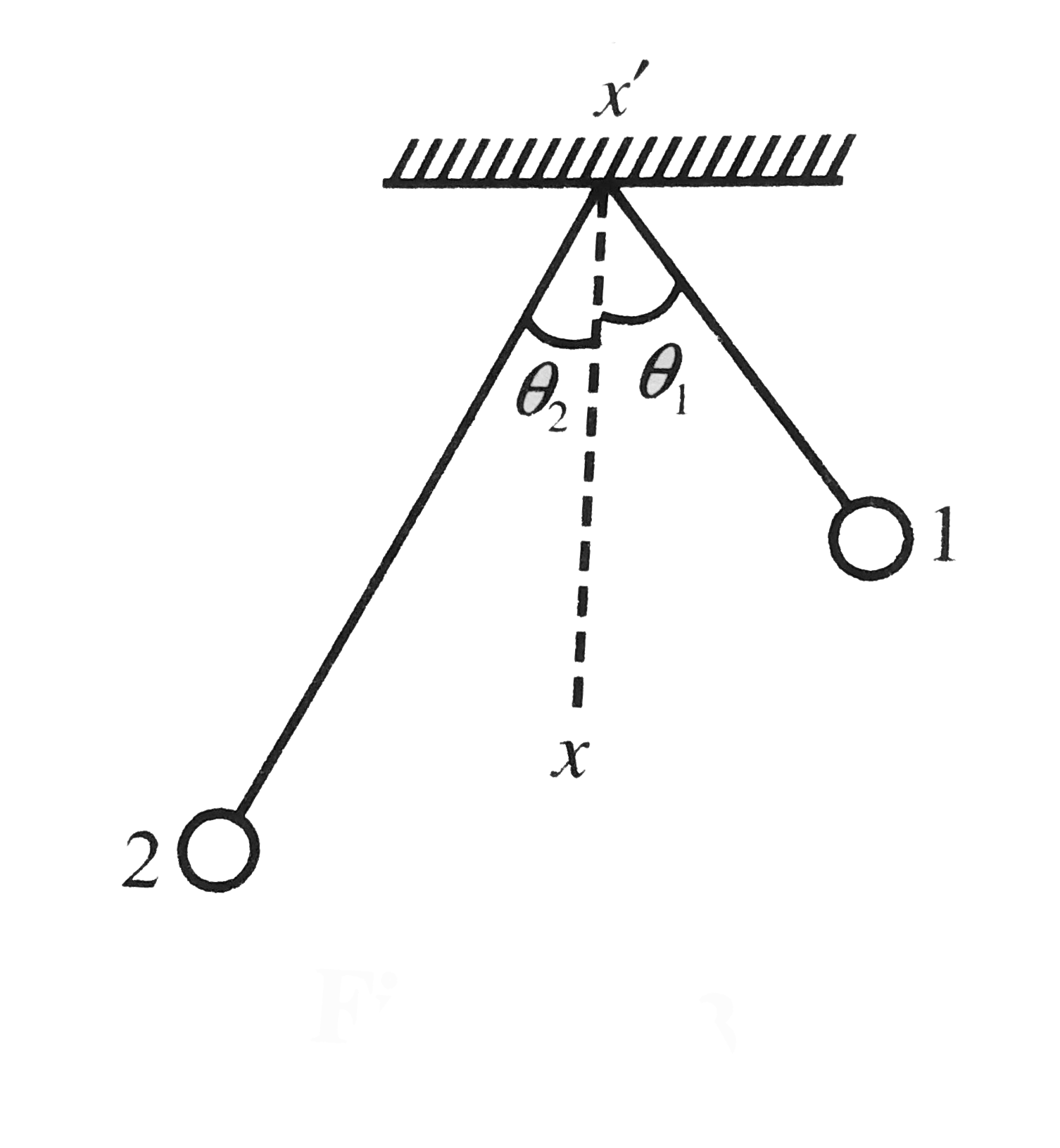
The angular positions of pendulums 1 and 2 are (takeing angles to the right of reference line to be positive)
(where
For the strings to be parallel for the first time
for ,
for ,,
Both the pendulums are parallel to each other for the first time after
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective type
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Comprehension
Explore 33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Two simple pendulum A and B having lengths l and l/4 respectively are released from the positions as shown in figure. Calculate the time after which the release of the two strings become parallel for the first time. Angle θ is very small.

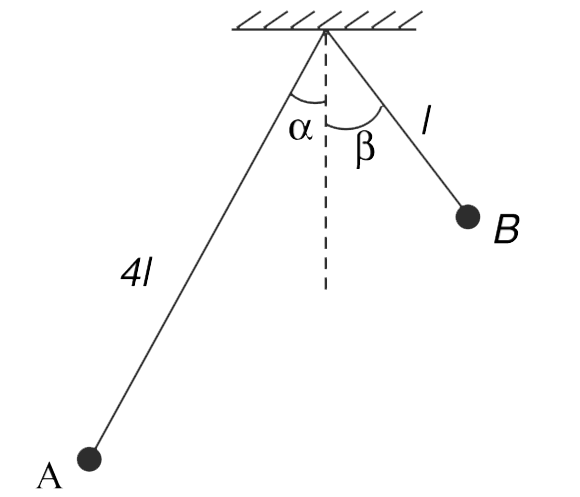
View SolutionTwo simple pendulums A and B have length 4l and l respectively. They are released from rest from the position shown. Both the angles α and β are small. Calculate the time after which the two string become parallel for the first time if-
(a) α=β " " (b)β=1.5α
View Solution
Knowledge Check
Two simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
A8π3√lgBπ3√lgC2sDNone of theseTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
A3:5B4:5C2:5D1:2Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
AL/3B3L/4C4L/3D5L/3
Two simple pendulums of length 1m and 1.21 m are started oscillating from some position. Find the minimum time (in second) after which they again start from same position.
View SolutionTwo simple pendulum have lengths land 25l16 . At t=0 they are in same phase after how may oscillations of smaller pendulum will they be again in phase for first time ?
View SolutionTwo balls are released from the same height at an interval of 2s. When will the separation between the balls be 20m after the first ball is released? Take g=10m/s2.
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution

