
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .
√3k2m+gl
√3k2m+3gl
√3km+3g2l
√3km+2g3l
The correct Answer is:C
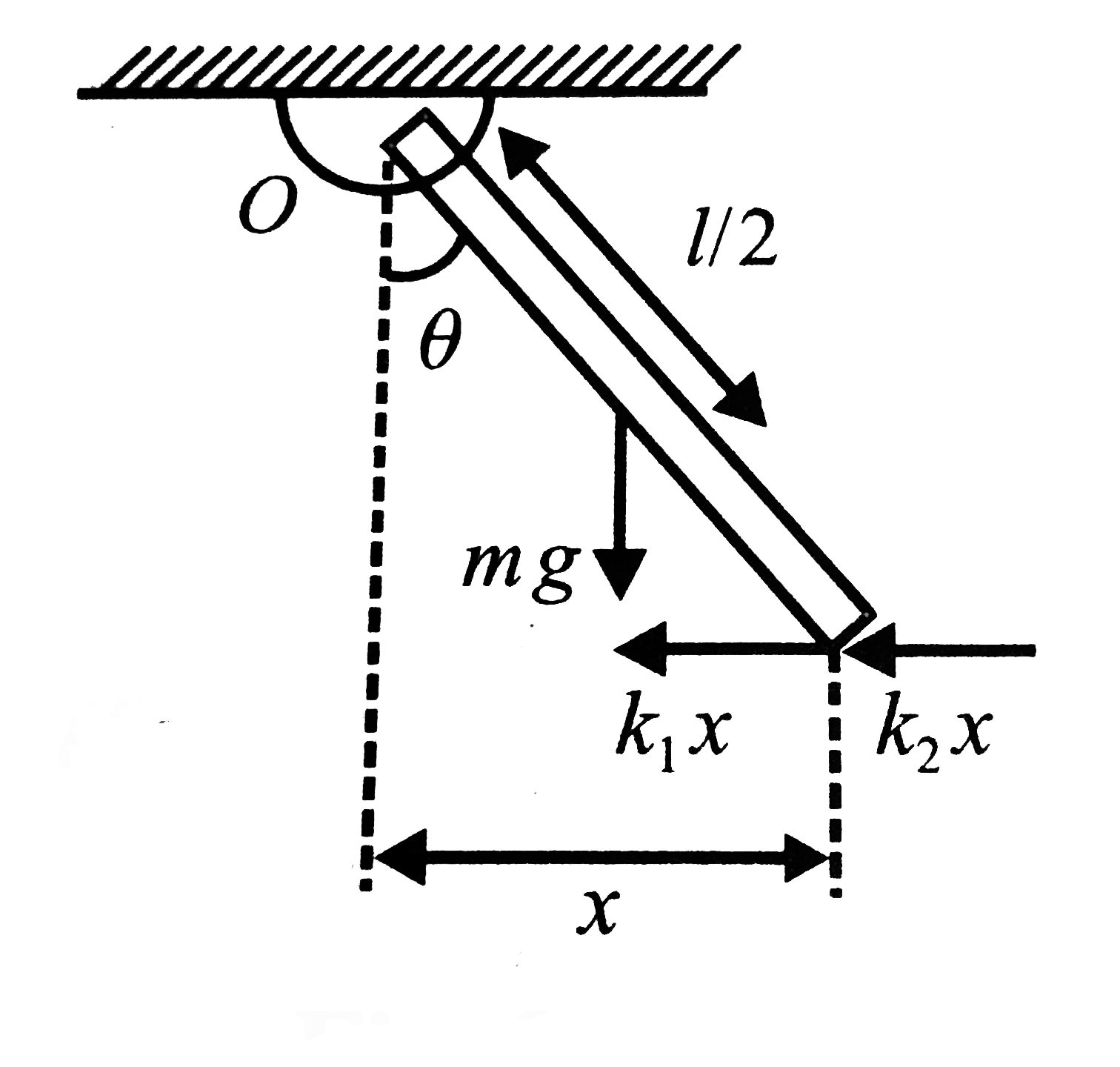
Let the bar be rotated through a small angle θ.
The restoring torque of the forces mg,k1x and k2x about O can be given as
τ=−[mg(12)sinθ+k1x(lcosθ)+k2x(lcosθ)]
Since θ is small, sinθ≅θ,x=<hη and cosθ=≅1 Putting k1+k2=k, we obtain
τ=−[kl2+mg(l2)]θ
or Iα=−[kl2+mg(l2)]θ
⇒ωOSC=
⎷⎛⎜
⎜⎝kl2+mg(l2)ml23⎞⎟
⎟⎠
=√3km+3g2l
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Find the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
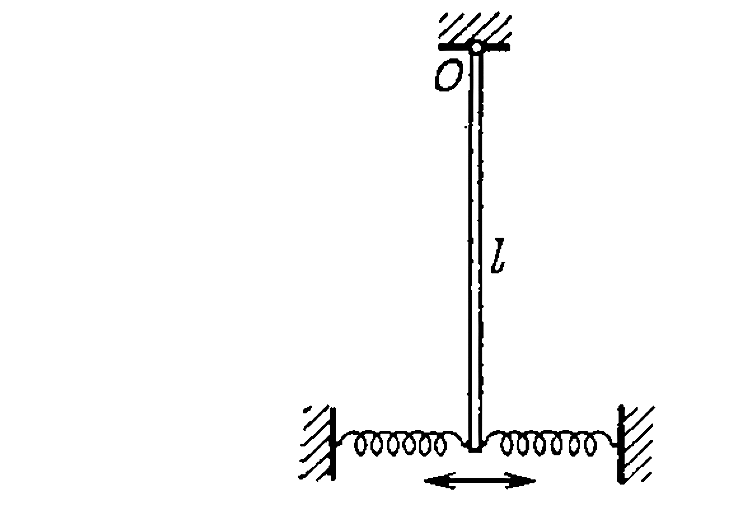
View SolutionFind the M.I. of thin uniform rod of mass M and length L about the axis as shown.

View Solution
Knowledge Check
A thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
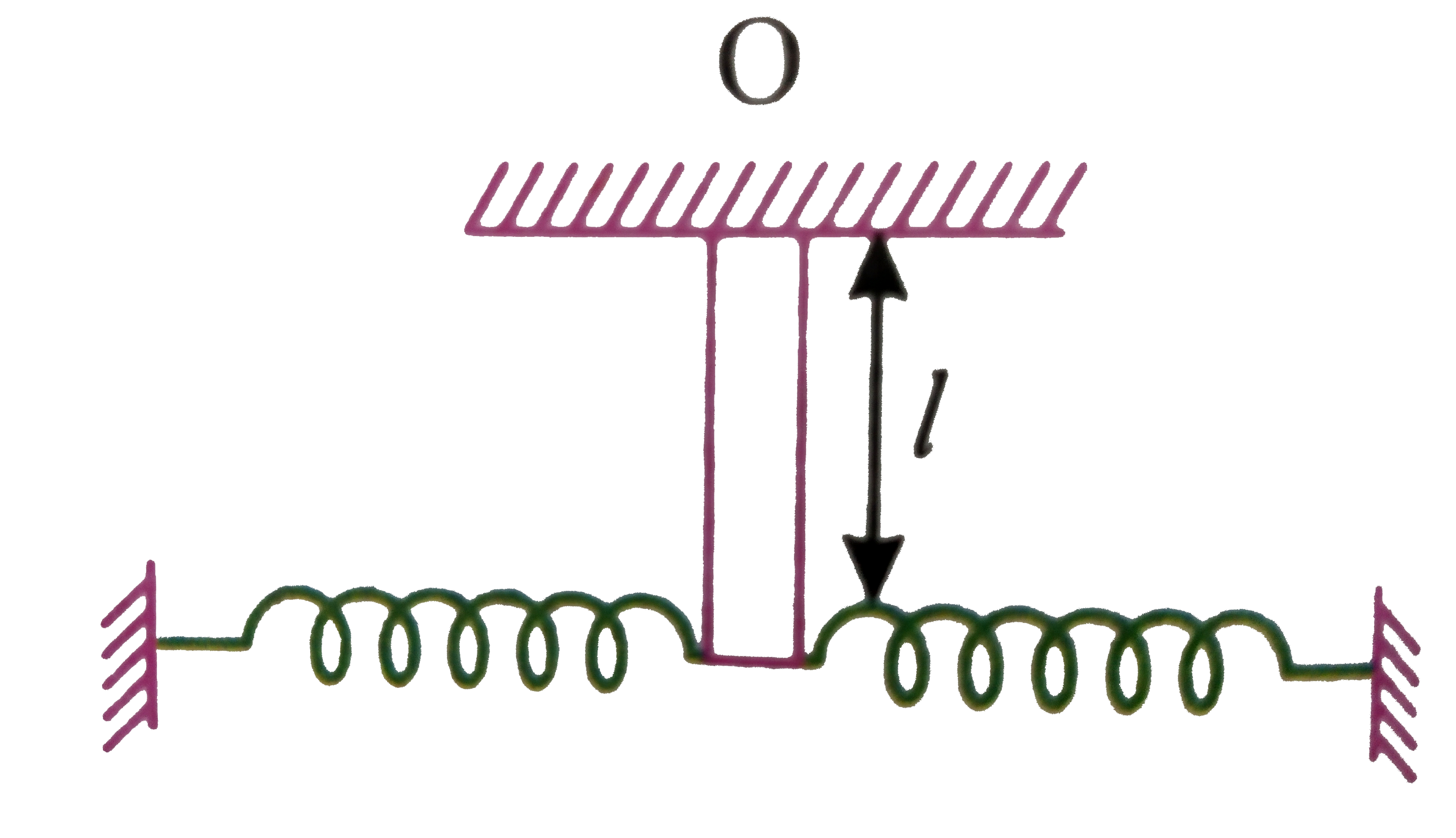 A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3lA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA body of mass m, is attached to a vertical rod of mass M nad length L, hung from a pivoted supprot. A springs of constant K fixed to a support on the left as shown and is attached to the rod at a distance form the pivot. The frequency of the oscillation is:
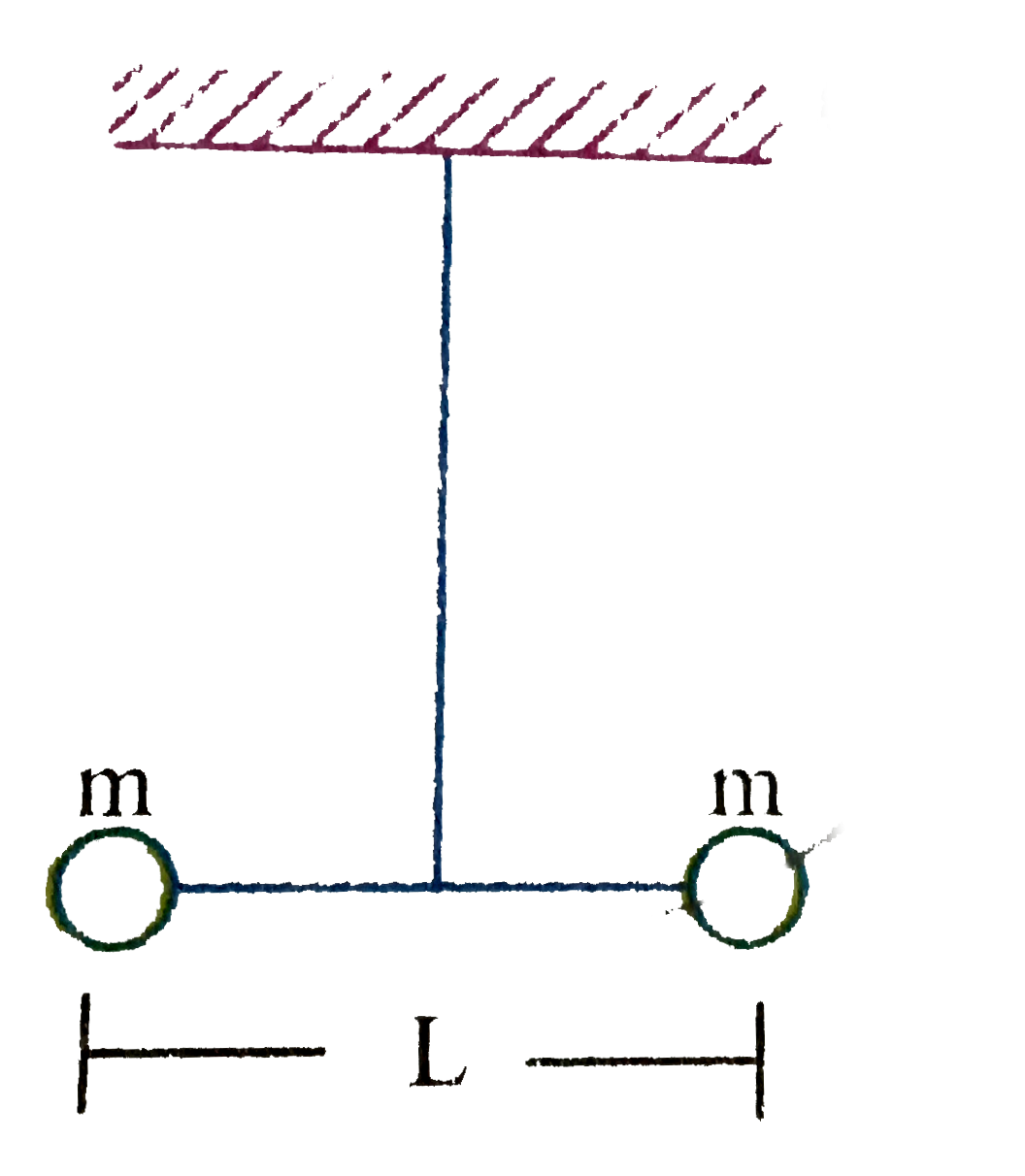 A12π√K(M+2m)B12π ⎷K(M3+2m)C2π ⎷K(M3+2m)D2π√M+2mK
A12π√K(M+2m)B12π ⎷K(M3+2m)C2π ⎷K(M3+2m)D2π√M+2mK
If the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
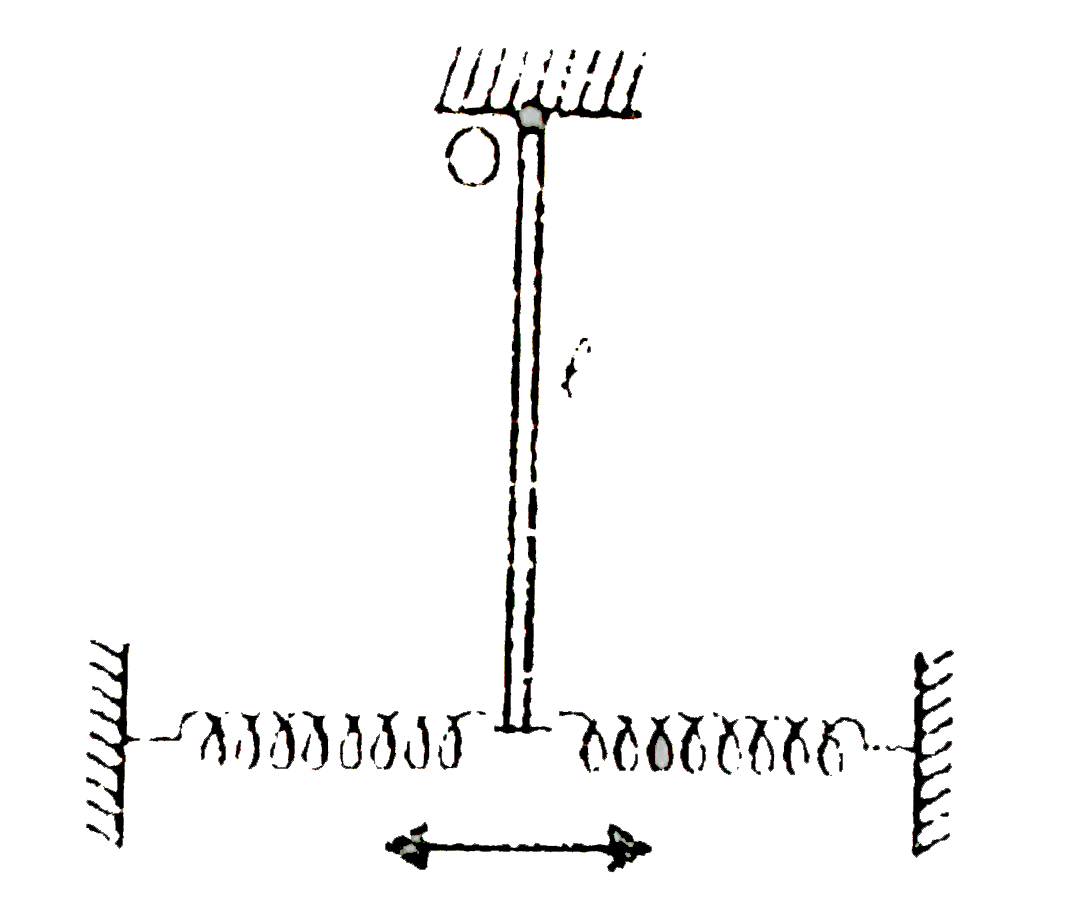
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
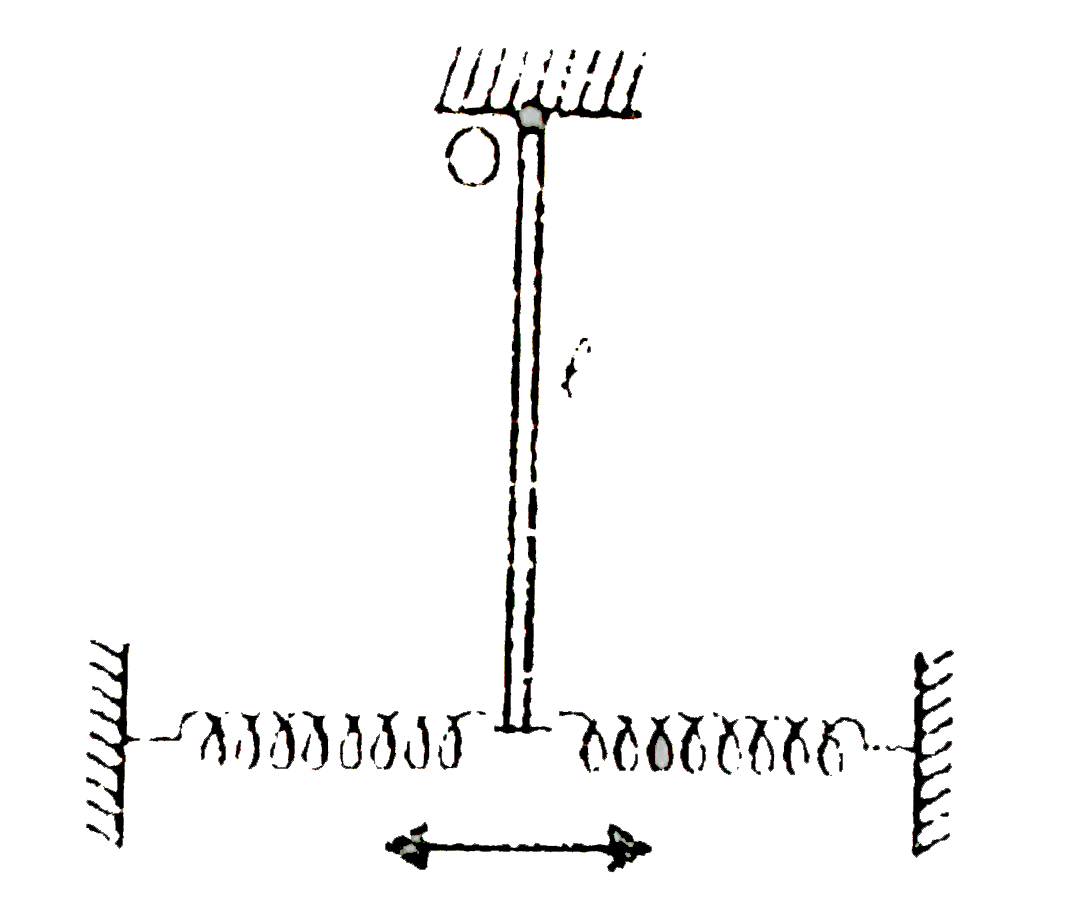
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
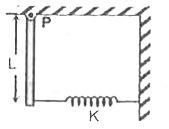
View SolutionA unifrom rod of mass m and length l0 is pivoted at one end and is hanging in the vertical at one end and is hagingh in the vertical direction.The period of small angular oscillations of the rod is

View Solution

