Find the M.I. of thin uniform rod of mass M and length L about the axis as shown.
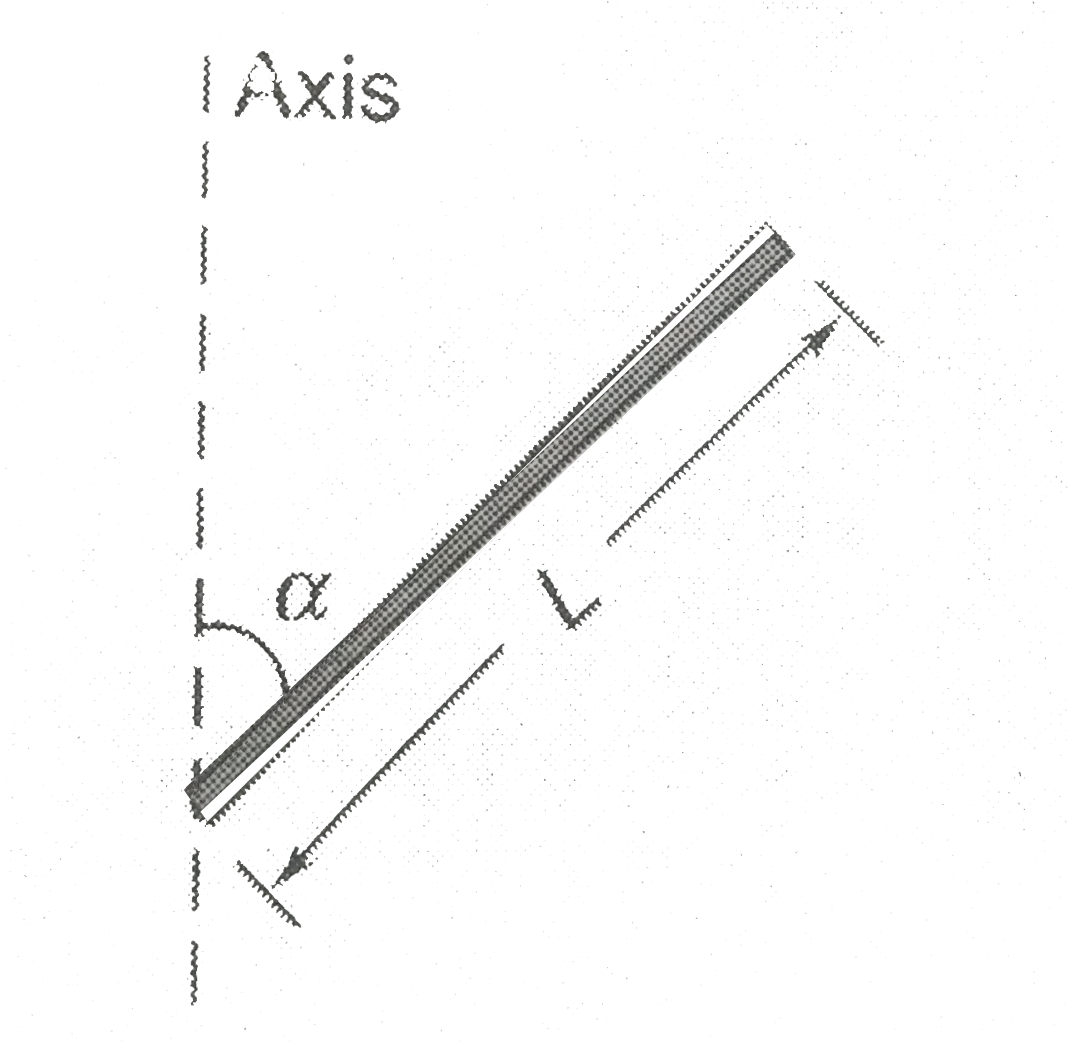

Here mass is distributed on length. Taking an element of small length dx at distance x as shown.
dm=MLdx
dI=r2dm=(xsinα)2MLdx
I=MLsin2α∫L0x2dx
=MLsin2α∣∣∣x33∣∣∣L0
=MLsin2αL33
13ML2sin2α
If α=90∘,I=13ML2
Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
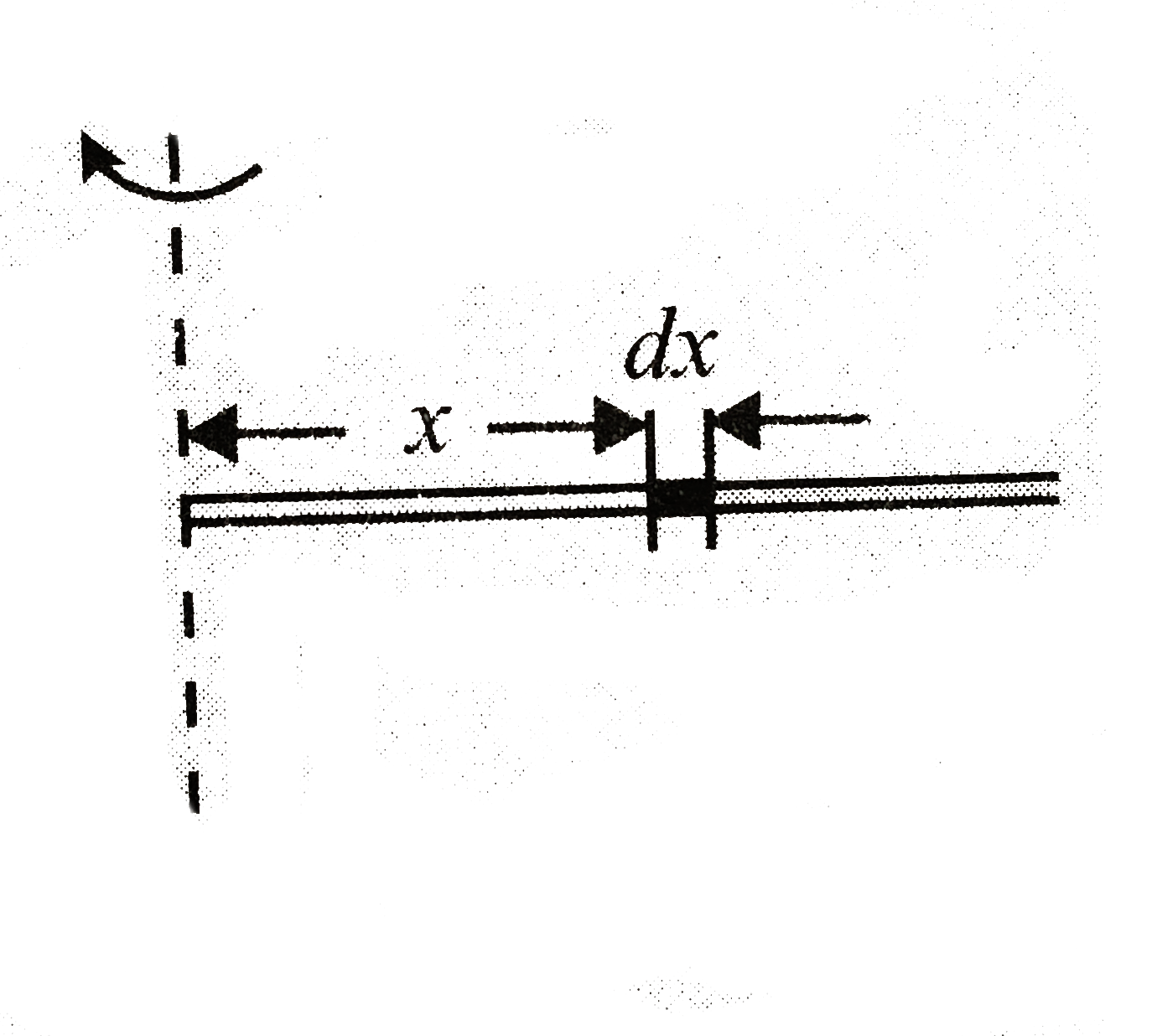
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution
Knowledge Check
The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
AI0+ML2/4BI0+2ML2CI0+ML2DI0+ML2/2The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0 . Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is
AI0+ML2/2BI0+ML2/4CI0+2ML2DI0+ML2
Figure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center.
(a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center?
(b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its eneds and perpendicular to its length.
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
View SolutionThe moment of inertia of a uniform thin rod of mass m and length L about two axis PQ and RS passing through centre of rod C and in the plane of the rod are IPQ and IRS respectively. Then IPQ+IRS is equal to
View Solution

