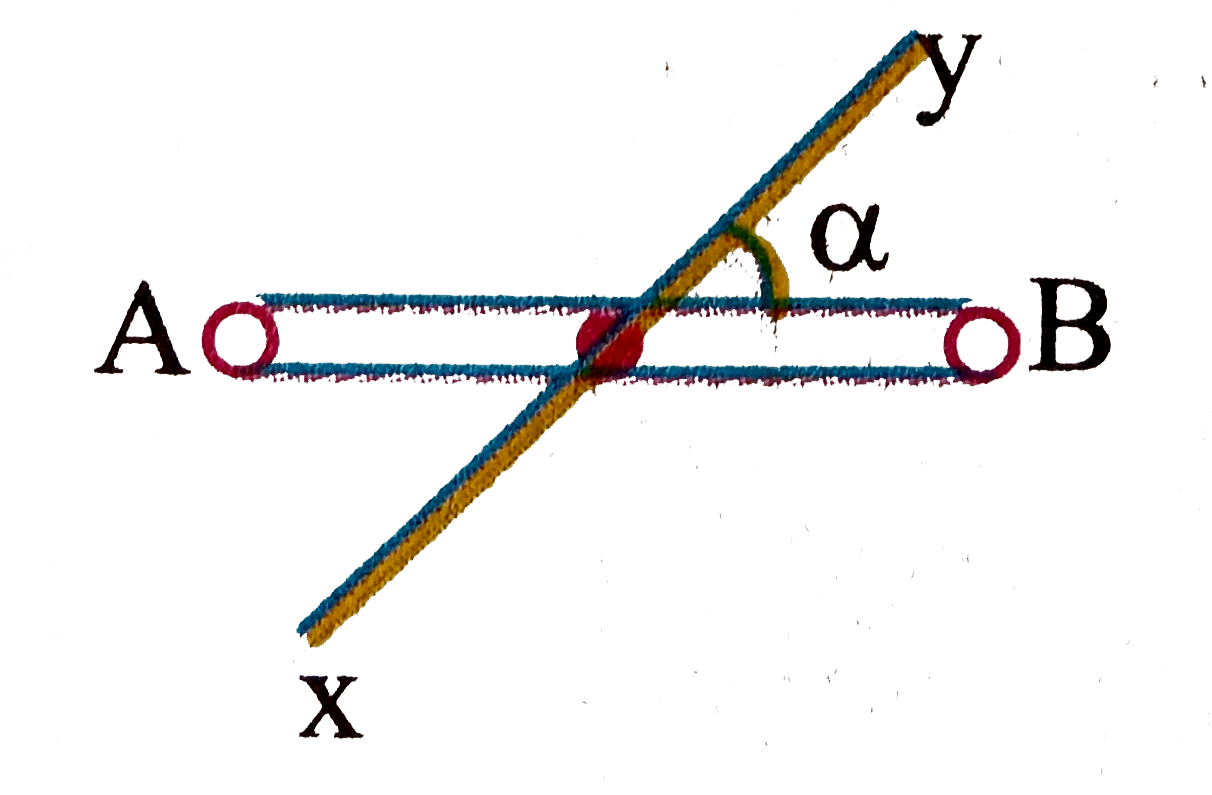
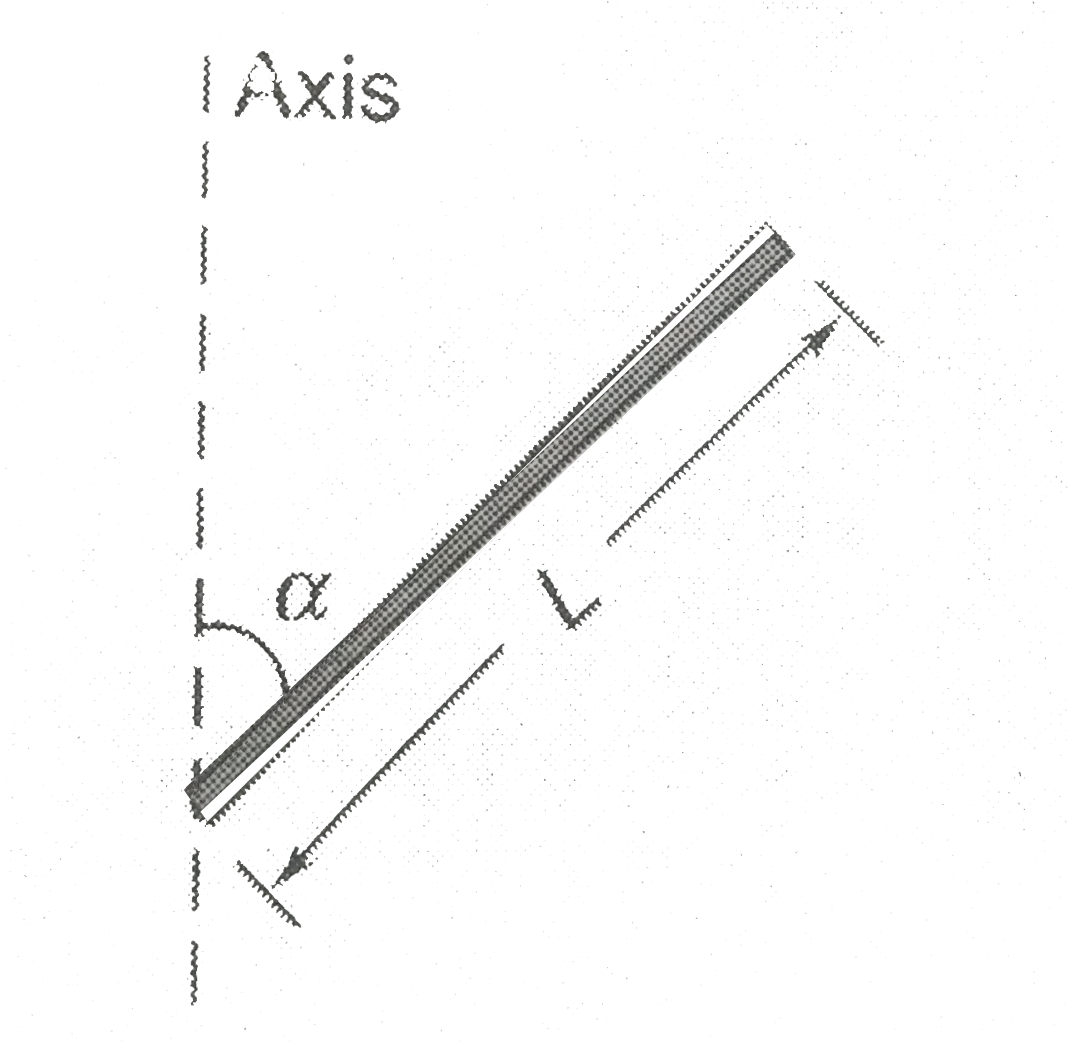The moment of inertia of a uniform thin rod of mass m and length L about two axis PQ and RS passing through centre of rod C and in the plane of the rod are $I_{P Q}$ and $I_{R S}$ respectively. Then $I_{P Q} + I_{R S}$ is equal to

A

$\frac{m l^{2}}{3}$

B

$\frac{m l^{2}}{2}$

C

$\frac{m l^{2}}{4}$

D

$\frac{m l^{2}}{12}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

The MI of rod about axis PQ figure (a) and MI of rod about axis P'Q' figure (b) are same by symmetry

$∴ I_{P Q} + I_{R S} = O_{P Q} + I_{R S} = \frac{m l^{2}}{12}$
by perpendicular axis theorem.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
A $\frac{m l^{2}}{12}$
B $\frac{m l^{2}}{3}$
C $\frac{7 m l^{2}}{48}$
D $\frac{m l^{2}}{9}$
Question 2 - Select One
Moment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
A $\frac{M L^{2}}{6}$
B $\frac{M L^{2}}{12}$
C $\frac{7 M L^{2}}{24}$
D $\frac{7 M L^{2}}{48}$
Question 3 - Select One
The moment of inertia of a uniform rod of length $2 l$ and mass $m$ about an axis $x y$ passing through its centre and inclined at an angle $α$ is

A $\frac{m l^{2}}{3} {sin}^{2} α$
B $\frac{m l^{2}}{12} {sin}^{2} α$
C $\frac{m l^{2}}{2} {cos}^{2} α$
D $\frac{m l^{2}}{2} {cos}^{2} α$

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.58

Home
Ask Doubt
Profile