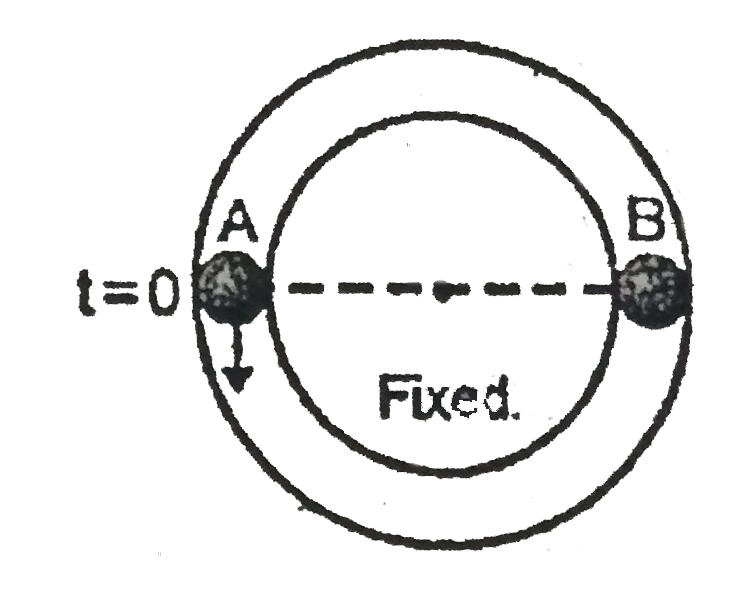
Particle 'A' moves with speed 10m/s in a frictionless circular fixed horizontal pipe of radius 5m and strikes with 'B' of double mass that of A. Coefficient of restitution is 12 and particle 'A' -starts its journey at t=0. The time at which second collision occurs is:
π2s
2π3s
5π2s
4πs
The correct Answer is:C
For first collision
v=10m/st1=π(5)10=π/2sec
velocity of sep = e velocity of opp.
v2−v1=12(10)⇒v2−v2=5m/s
for second collision
∴t2=2π(5)5=2π
∴ total time t=t+t2=π/2+2π
t=2.5π
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.59
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.60
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.57
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Two particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Loss in kinetic energy in collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View Solution
Knowledge Check
A ball falls from a height of 10m on to a horizontal plane. If the coefficient of restitution is 0.4, then the velocity with which it rebounds from the plane after second collision is
A2.24ms−1B5.6ms−1C2.8ms−1D0.9ms−1A particle moving with a velocity of (4ˆi−ˆj ) mis strikes a fixed smooth wall and finally moves with a velocity of (3ˆi+2ˆj) m/s. The coefficient of restitution between the wall and the particle in the collision will be
A73B37C√1317D√1713A particle moves with a speed of 1.5×108 m/s. The ratio of its mass to its rest mass is
A1.1B1.5C2.5D5.2
Two particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
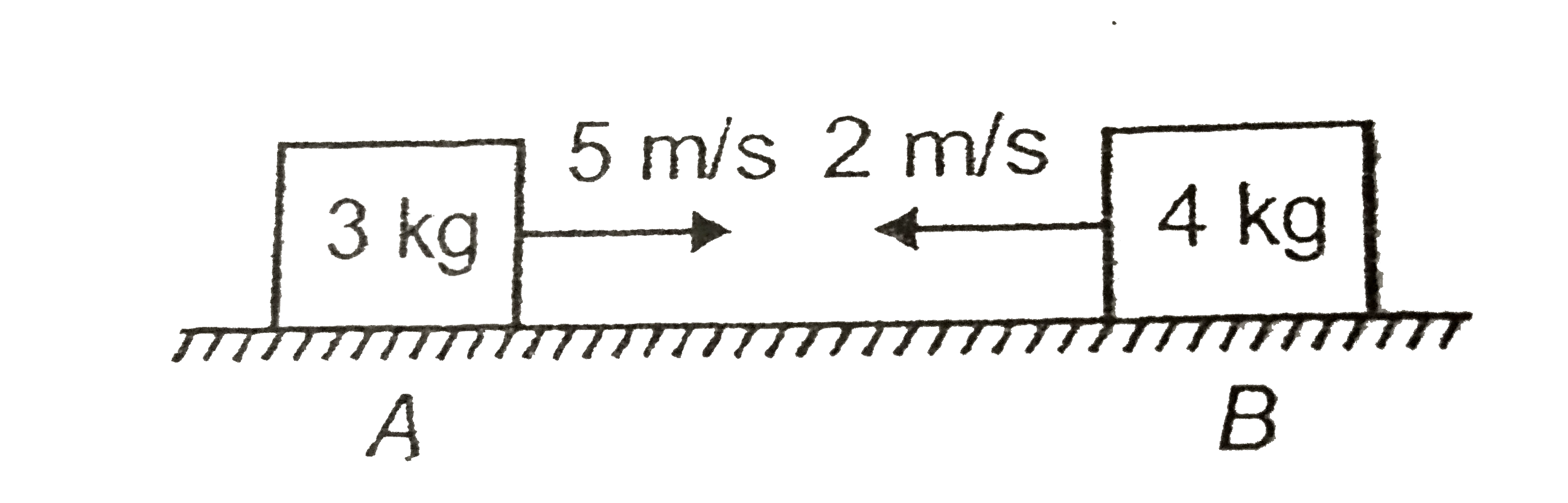
Velocity of A after collision
View SolutionIf a particle moves with a speed of 1.5×108 m/s then the ratio of its mass to its rest mass is
View SolutionA particle dropped from a height of 100 m, collides with the horizontal surface where coefficient of restitution is 0.5, the velocity attained by the particle in 5th collision is
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
View Solution

