Two semicircular rings of linear mass densities λ and 2λ and of radius 'R' each are joined to form a complete ring. The distance of the centre of the mass of complete ring from its geometrical centre is :
3R8π
2R3π
3R4π
None of these
The correct Answer is:B
Let the two half rings be placed in left and right of y-axis centre as shown in the figure.
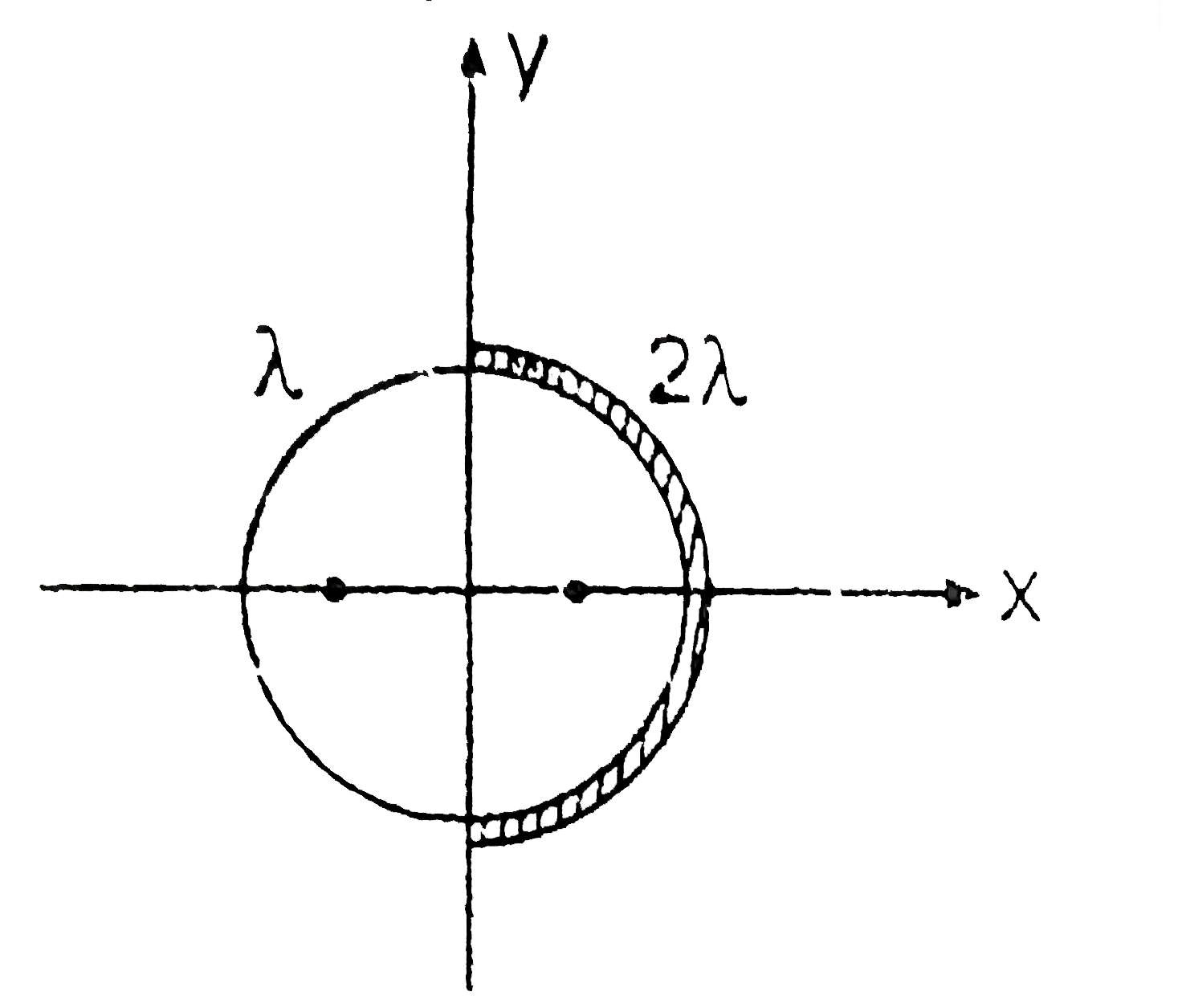
Then the coordinate of centre of mass of left and right rings are (−2Rπ,0) and (2Rπ,0)
∴ x-coordinates of centre of mass of complete ring is m(−2Rπ)+2m(2Rπ)3m=2R3π.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.59
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.60
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.57
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Knowledge Check
What is the distance of centre of mass of a half fring from centre if the ring has radius =0.5 m [XI]
A1πB13πC23πD12πA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2The moment of inertia of semicircular ring about its centre is
AMR2BMR22CMR24DNone of these
Find the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
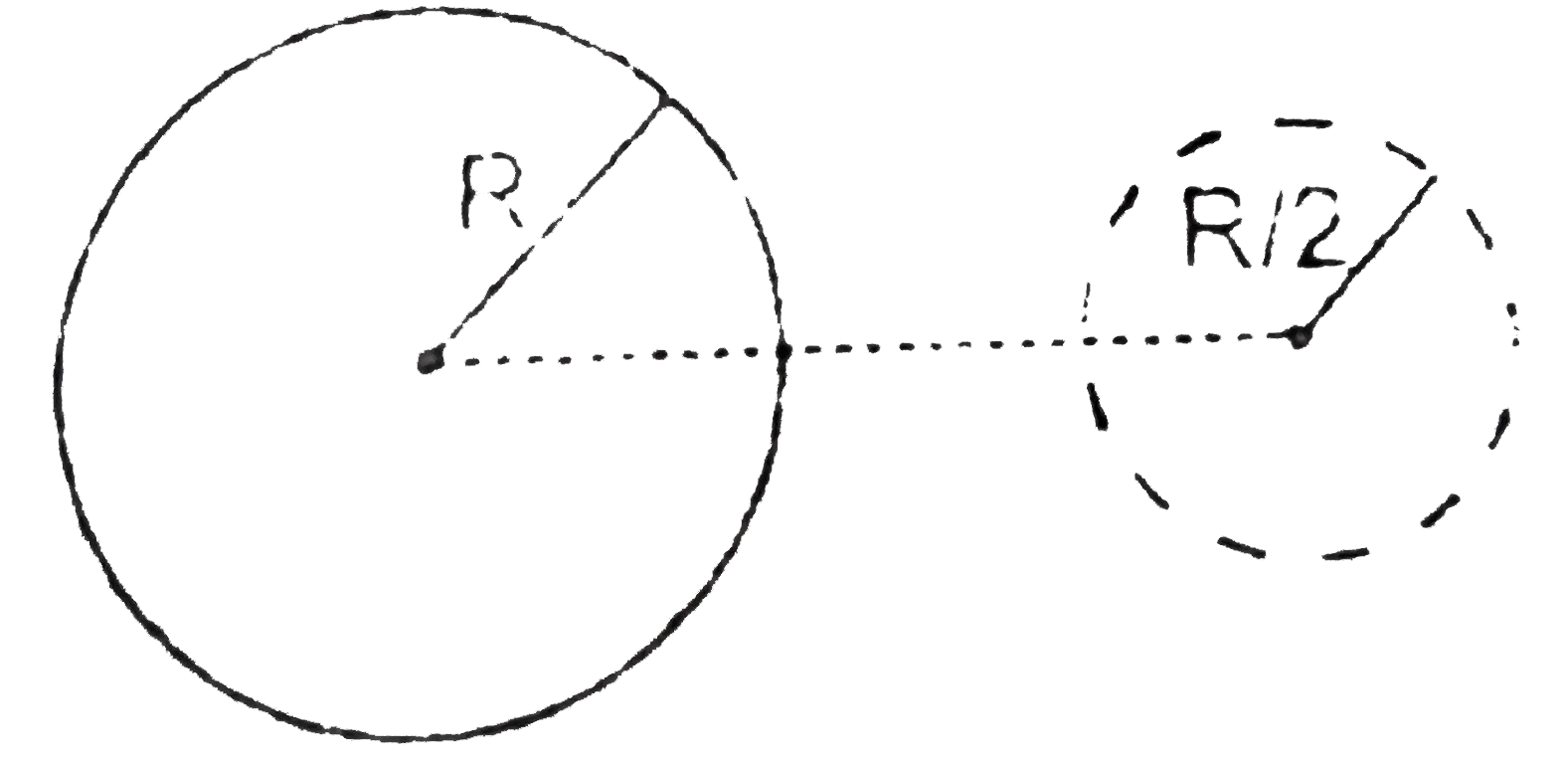
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
View SolutionThe escape velocity form the centre of a unifrom ring of mass M and radius R is :
View Solution

