The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is

(3/2)MR2
(3/4)MR2
MR2(1+1/√2)
MR2/(2√2)
The correct Answer is:B
Related Playlists
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.599videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.609videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.579videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions

Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is LView Solution
Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is LView SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
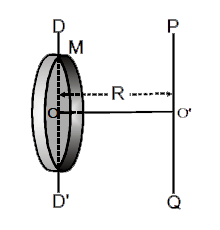 View Solution
View SolutionCalculate the moment of inertia of a thin rod of mass m and length l about a symmetry axis through the centre of mass and perpendicular to the length of the rod, as shown in Fig.
 View Solution
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View Solution

