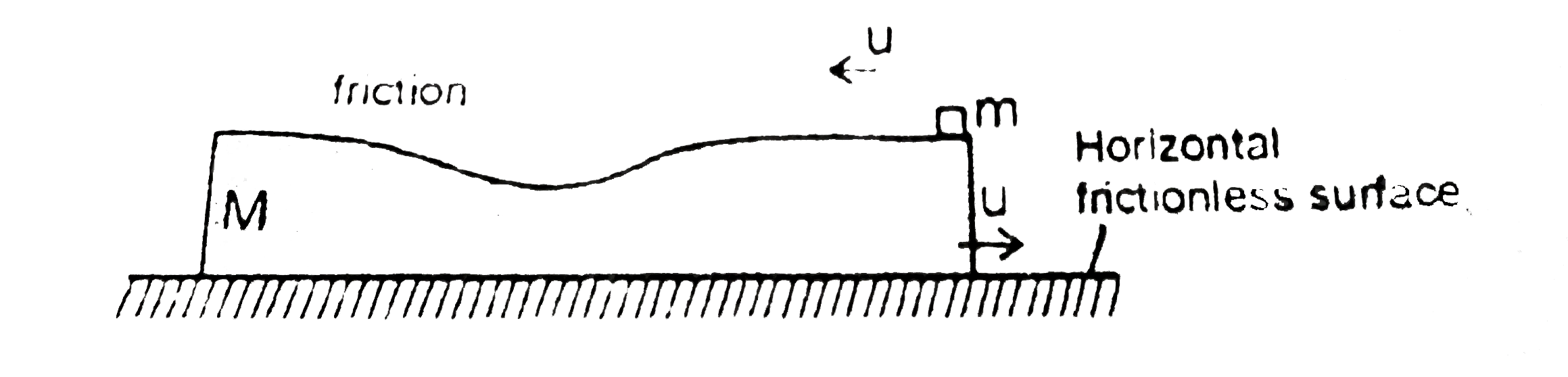
A small block of mass 'm' is placed on bigger block of mass M1 which is placed on a fractionless horizontal surface. The two blocks are given equal speed u1 but opposite directions, as shown in the figure. After sometime, it is observed that both blocks are moving in the direction of motion of the lower block, with a speed greater than u2. It can be concluded that -
M>3m
3M<m
m>2M
M,m can have any value such that M>m
The correct Answer is:A
Conserving linear momentum in horizontal direction w.r.t ground
Mu−μ=(M+m)v
It v>u2⇒(M−m)(M+m)u>u2
⇒(M−m)(M+m)>12,⇒M>3m
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.59
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.60
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.57
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
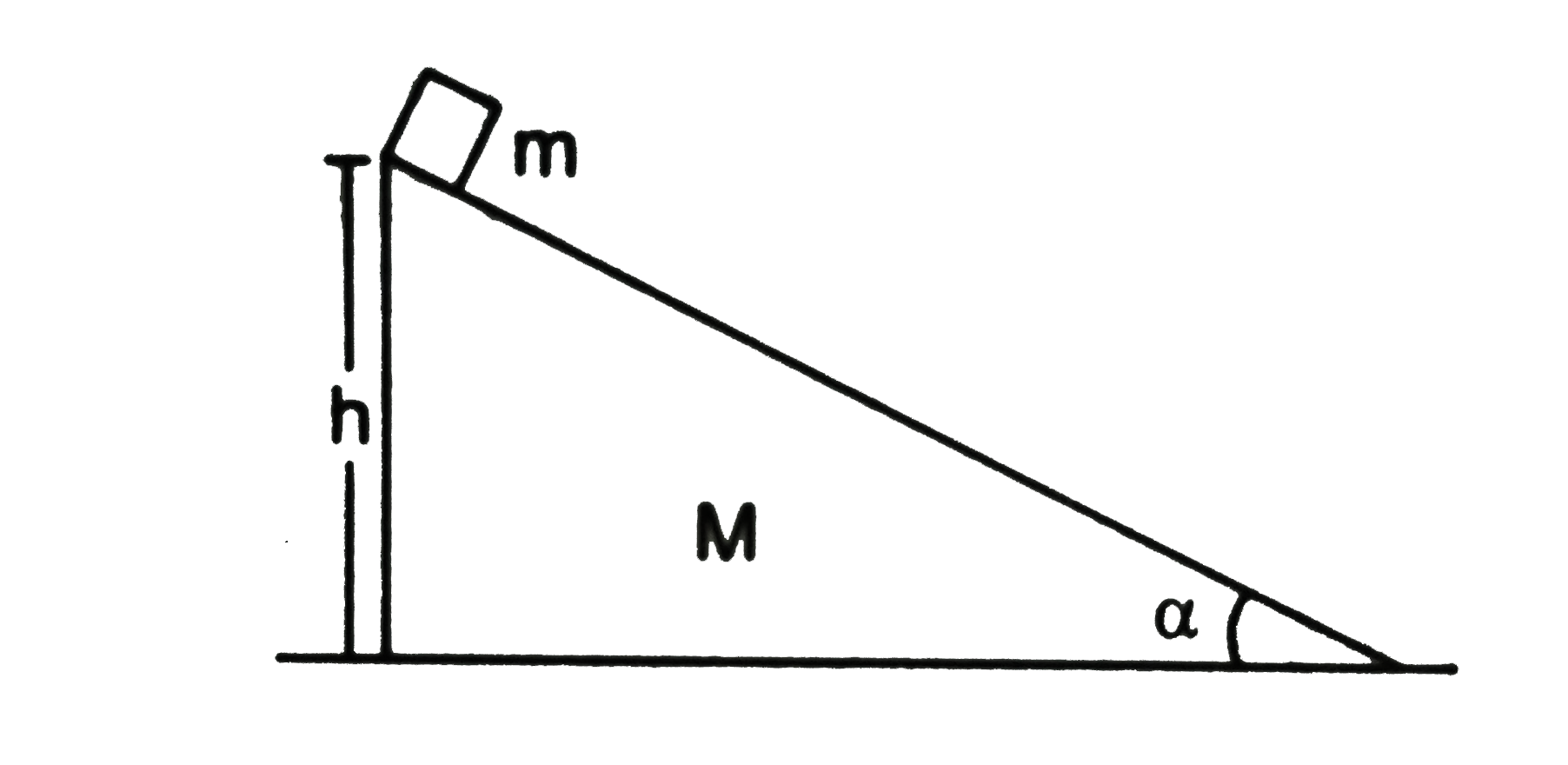
A block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
View SolutionTwo identical blocks each of mass 1kg are joined together with a compressed spring. When the system is released the two blocks appear to be moving with unequal speeds in the opposite directions as shown in fig.
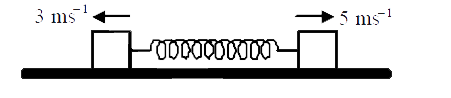
Choose the correct statement -
View Solution
Knowledge Check
A small block of mass 'm' is placed on bigger block of mass M1 which is placed on a fractionless horizontal surface. The two blocks are given equal speed u1 but opposite directions, as shown in the figure. After sometime, it is observed that both blocks are moving in the direction of motion of the lower block, with a speed greater than u2. It can be concluded that -
 AM>3mB3M<mCm>2MDM,m can have any value such that M>m
AM>3mB3M<mCm>2MDM,m can have any value such that M>mBlocks A and B are resting on a smooth horizontal surface given equal speeds of 2ms−1 in opposite sense as shown in the figure.
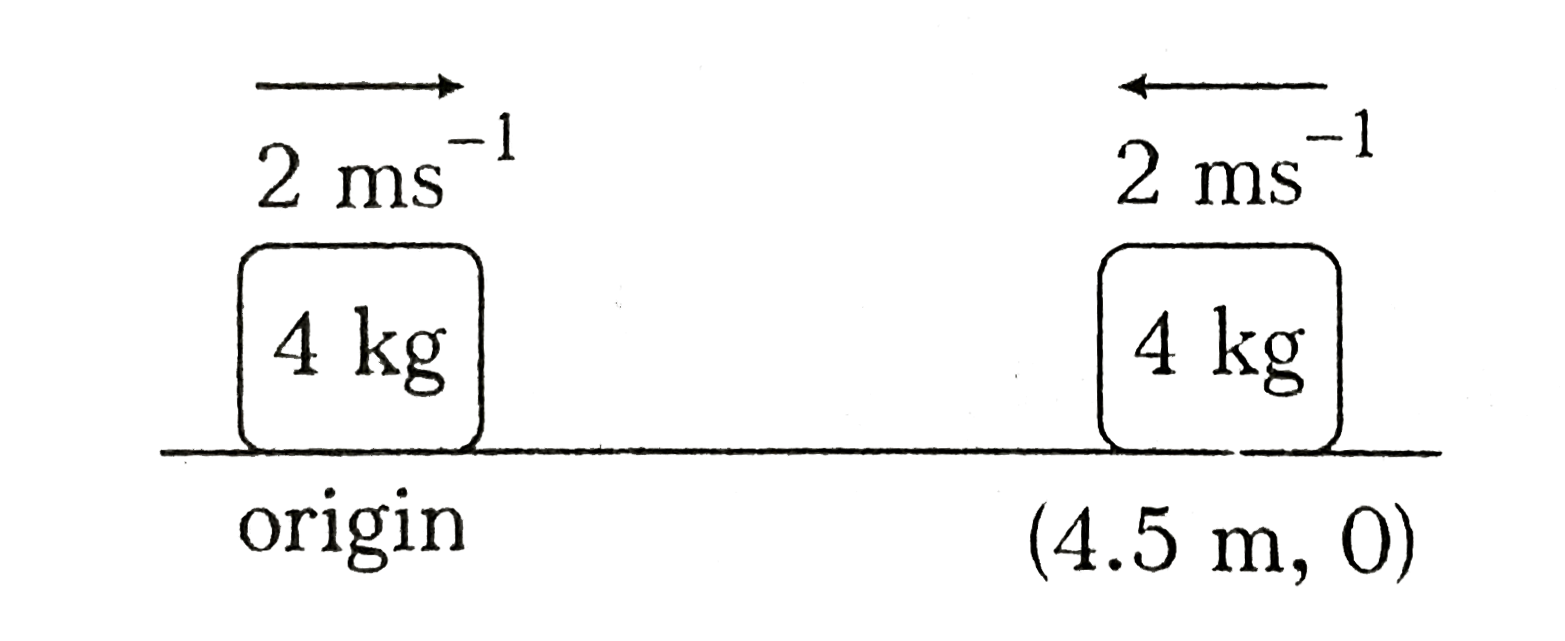
At t=0, the position of blocks are shown, then the coordinates of center of mass t=3s will beA(1,0)B(3,0)C(5,0)D(2.25,0)A block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?
 A(M+m)(μ2−μ1)gB(M−m)(μ2−μ1)gC(M−m)(μ2+μ1)gD(M+m)(μ2+μ1)g
A(M+m)(μ2−μ1)gB(M−m)(μ2−μ1)gC(M−m)(μ2+μ1)gD(M+m)(μ2+μ1)g
A small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
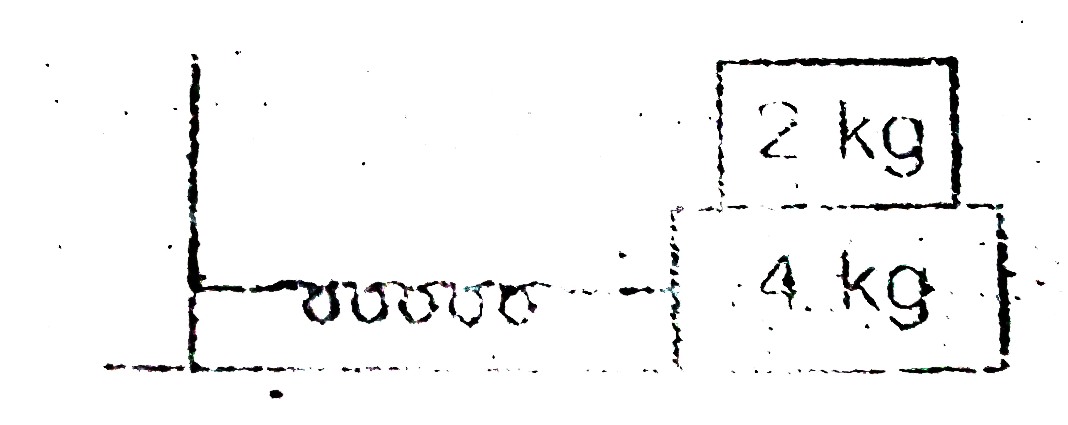
View SolutionA block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

View SolutionA block of mass 2 kg is plased on a smooth horizontal surface. Two forces F1=20 N and F2=5 N start acting on the block in opposite directions as shown. If block gets displaced by 5 m in the direction of net force then work done by F2 is :-

View SolutionA body of mass M with a small block m placed on it rests on a smooth horizontal surface. The block is set in motion in the horizontal direction with a velocity v. To what height relative to the initial level will the block rise after breaking off from the body M. Friction can be assumed to be absent.

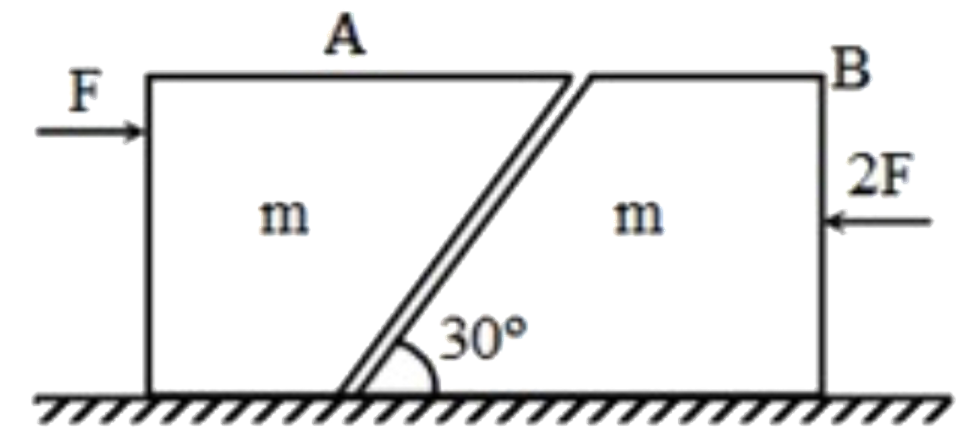
View SolutionTwo blocks 'A' and 'B' each of mass 'm' are placed on a smooth horizontal surface . Two horizontal force F and 2F are applied on the blocks A and B , respectively , as shown in figure . The block A does not slide on block B . The normal reaction acting between the two blocks is
View Solution
