A block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

When the smaller block reaches at bottom
V:vM/g
v:vm/M
vm/g in horizontal direction =vcos30∘−V
vm/g in vertical direction =vsin30∘
By the momentum conservation in the horizontal direction
m(vcos30∘−V)=MV=2mV
3V=vcos30∘=√3v2⇒v=2√3V
By the energy conservation
mgH=12m(vcos30∘−V)2
+12m(vsin30∘)2+12MV2
=12m(2V)2+12m(2V√3×12)2+12×2mV2
=2mV2+3mV22+mV2=92mV2
V=√2gH9=√2gH3

Topper's Solved these Questions
Similar Questions
A block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
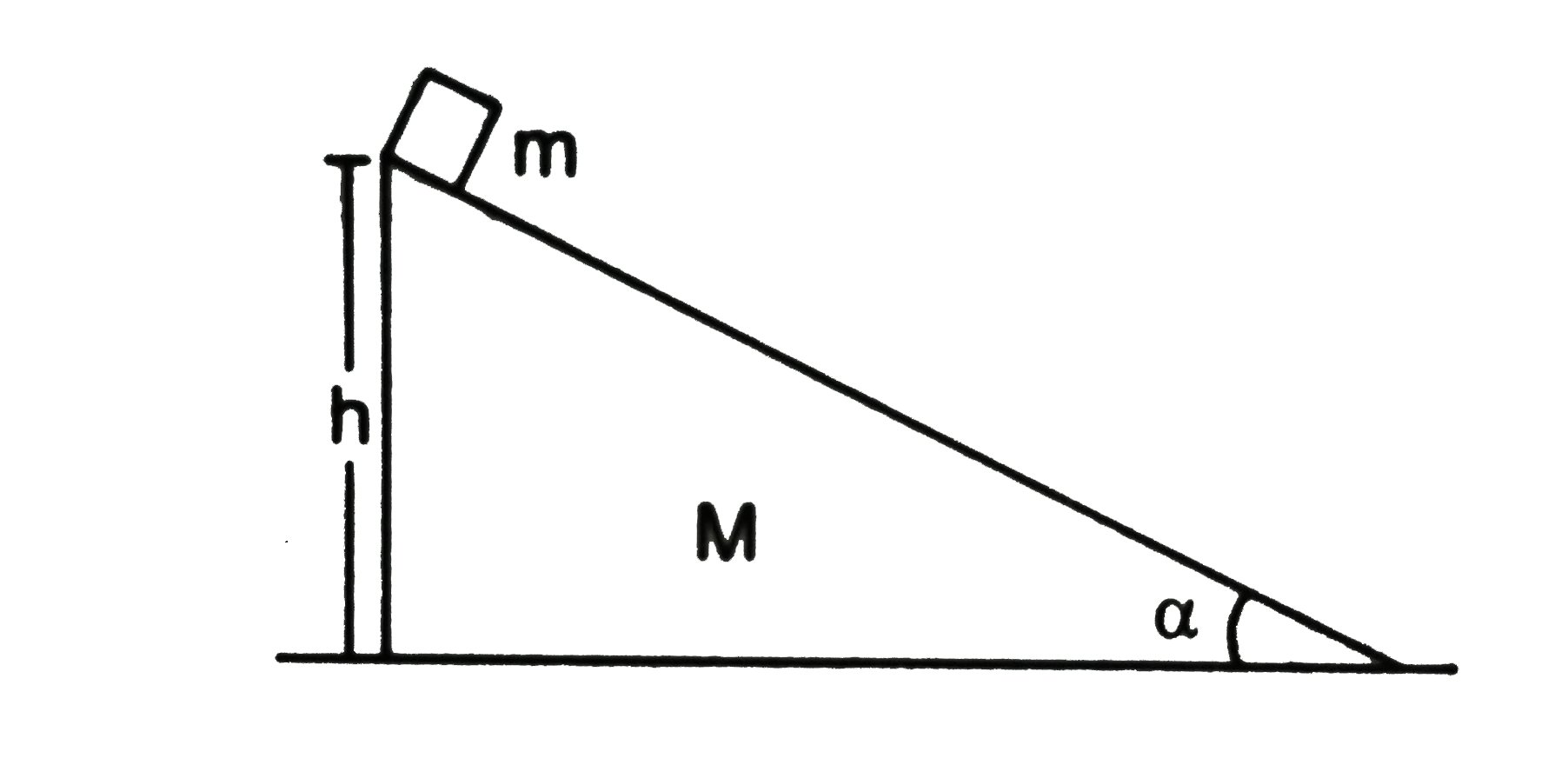
View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View Solution
Knowledge Check
A block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
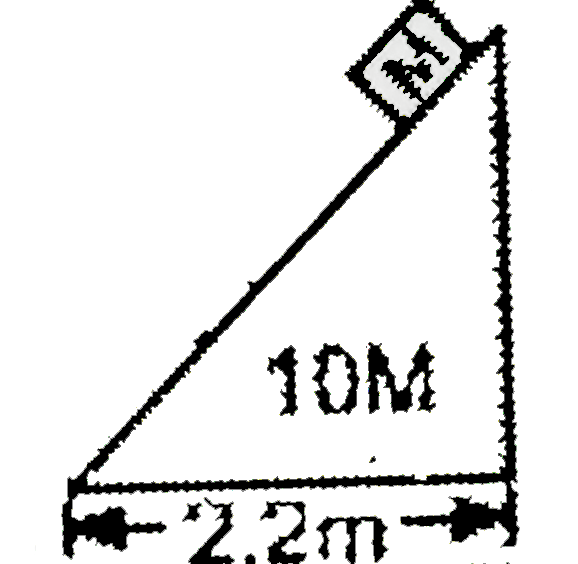 A0.22 mB0.20 mCzeroD0.24 m
A0.22 mB0.20 mCzeroD0.24 mA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
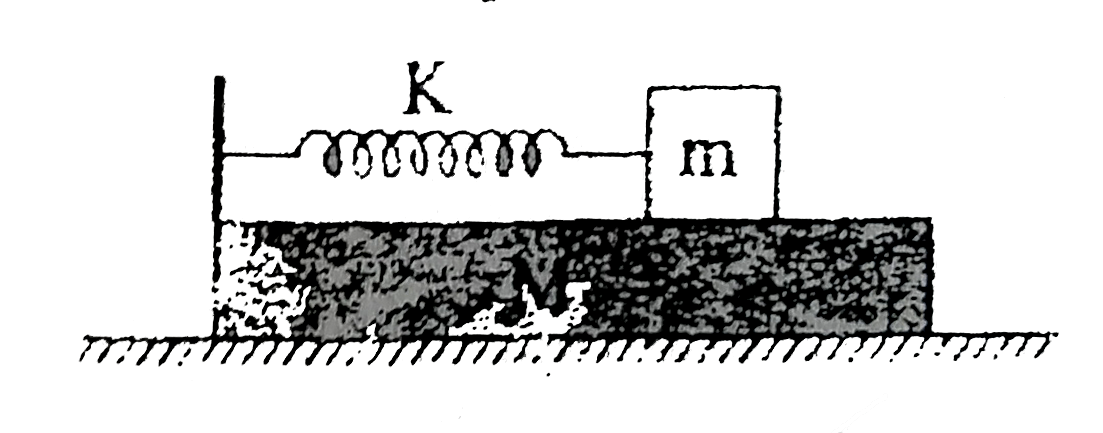 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0A block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
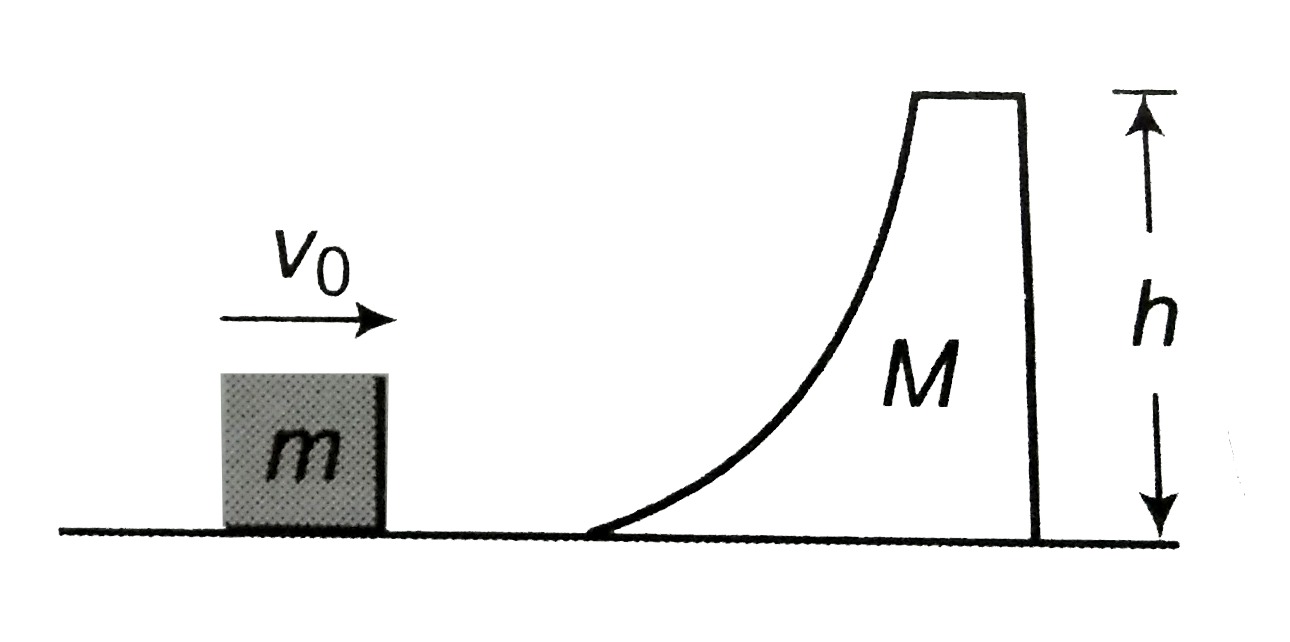 A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
Assuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

View SolutionA block of mass m is placed on a wedge of mass M and a force F is acting on its as shown . If all surfaces are smooth , find the force F such that, there is no relative motion between m and M.
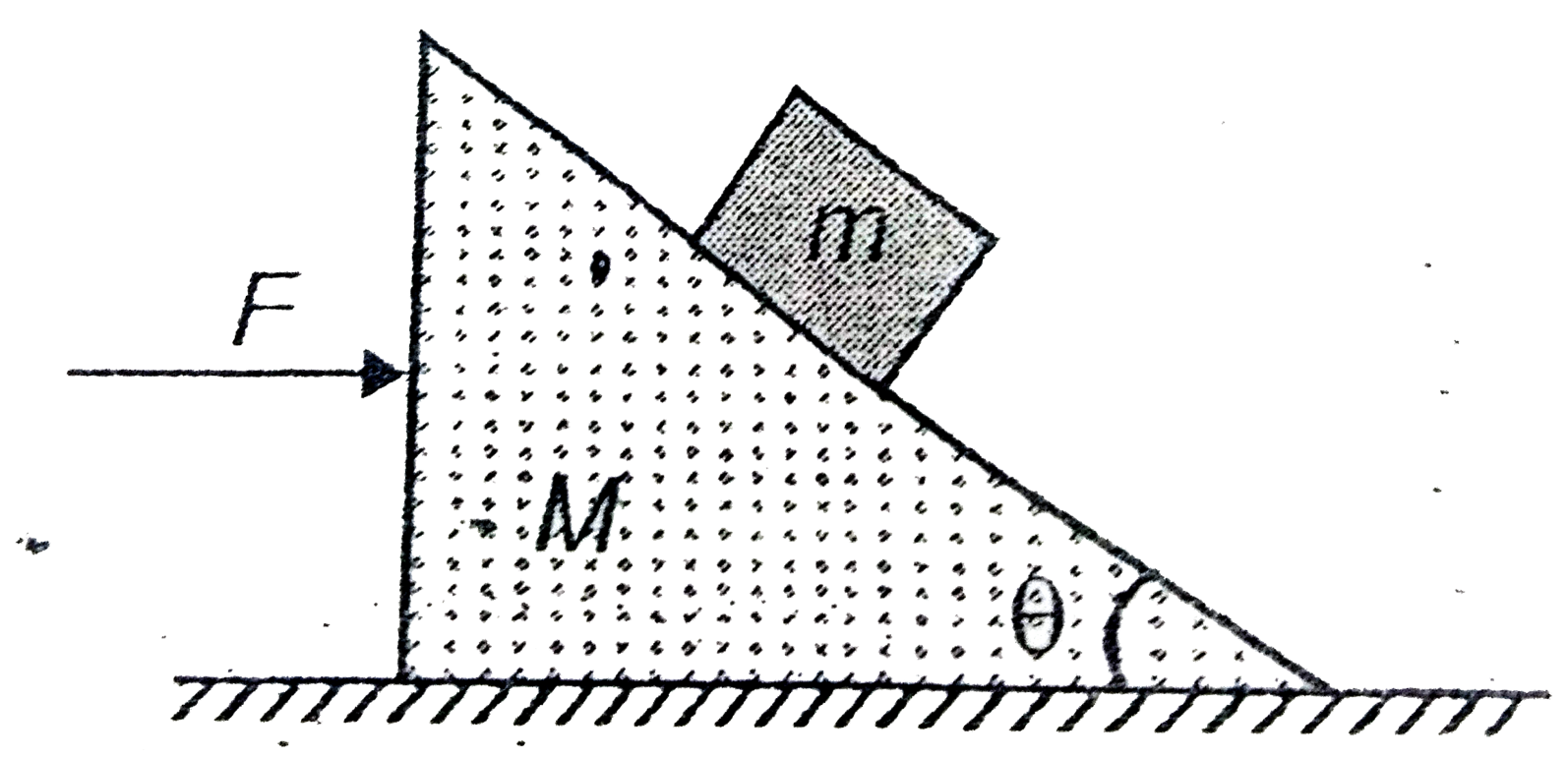
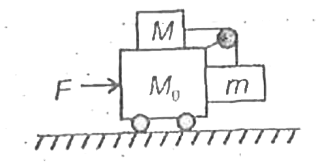
View SolutionTwo blocks of mass M and m are kept on the trolley whose all surfaces are smooth select the correct statement
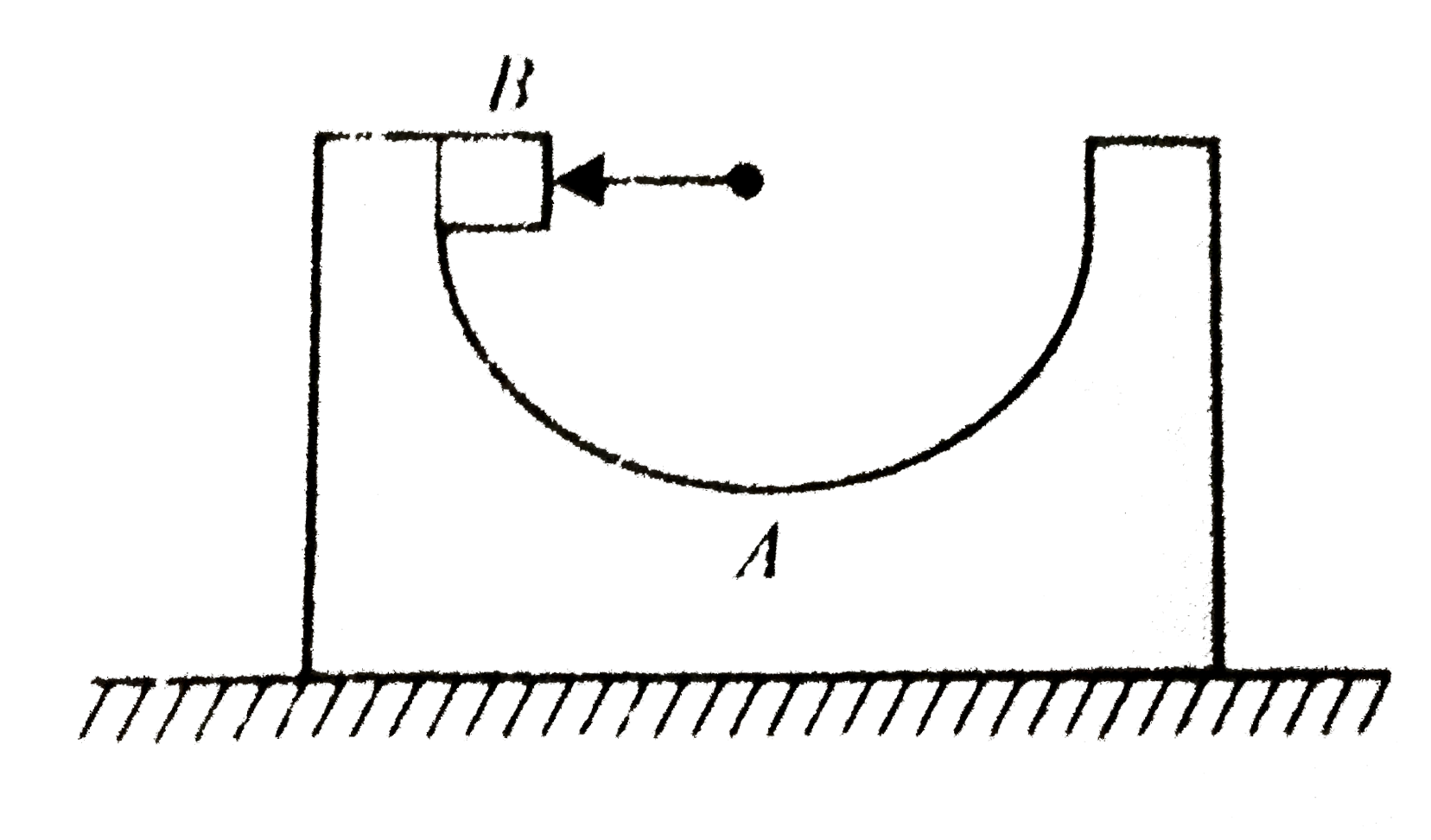
View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View Solution

