A pulley fixed to the ceiling carries a string with blocks of mass m and 3m attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
0
g/4
g/2
−g/2
The correct Answer is:B
To find the acceleration of the center of mass of the system consisting of two blocks of masses m and 3m connected by a string over a pulley, we can follow these steps:
Step 1: Identify the forces acting on the system
When the system is released, the block of mass 3m will accelerate downward due to gravity, while the block of mass m will accelerate upward. The gravitational force acting on each block is given by:
- For block m: \( F_1 = mg \) (upward)
- For block 3m: \( F_2 = 3mg \) (downward)
Step 2: Calculate the net force acting on the system
The net force acting on the system can be calculated by considering the difference between the downward force and the upward force:
\(
F_{net} = F_2 - F_1 = 3mg - mg = 2mg
\)
Step 3: Determine the total mass of the system
The total mass of the system is the sum of the masses of both blocks:
\(
M_{total} = m + 3m = 4m
\)
Step 4: Apply Newton's second law to find the acceleration
According to Newton's second law, the acceleration \( a \) of the center of mass can be calculated using the formula:
\(
a = \frac{F_{net}}{M_{total}} = \frac{2mg}{4m}
\)
Simplifying this gives:
\(
a = \frac{2g}{4} = \frac{g}{2}
\)
Step 5: Determine the direction of acceleration
Since the net force is directed downward (due to the heavier block), the acceleration of the center of mass will also be downward. Therefore, we can express the acceleration as:
\(
a = \frac{g}{2} \text{ (downward)}
\)
Final Answer
The acceleration of the center of mass of the system is \( \frac{g}{2} \) downward.
---
When the system is released, the block of mass 3m will accelerate downward due to gravity, while the block of mass m will accelerate upward. The gravitational force acting on each block is given by:
- For block m: \( F_1 = mg \) (upward)
- For block 3m: \( F_2 = 3mg \) (downward)
The net force acting on the system can be calculated by considering the difference between the downward force and the upward force:
\(
F_{net} = F_2 - F_1 = 3mg - mg = 2mg
\)
The total mass of the system is the sum of the masses of both blocks:
\(
M_{total} = m + 3m = 4m
\)
According to Newton's second law, the acceleration \( a \) of the center of mass can be calculated using the formula:
\(
a = \frac{F_{net}}{M_{total}} = \frac{2mg}{4m}
\)
Simplifying this gives:
\(
a = \frac{2g}{4} = \frac{g}{2}
\)
Since the net force is directed downward (due to the heavier block), the acceleration of the center of mass will also be downward. Therefore, we can express the acceleration as:
\(
a = \frac{g}{2} \text{ (downward)}
\)
The acceleration of the center of mass of the system is \( \frac{g}{2} \) downward.
Topper's Solved these Questions
Similar Questions
A pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
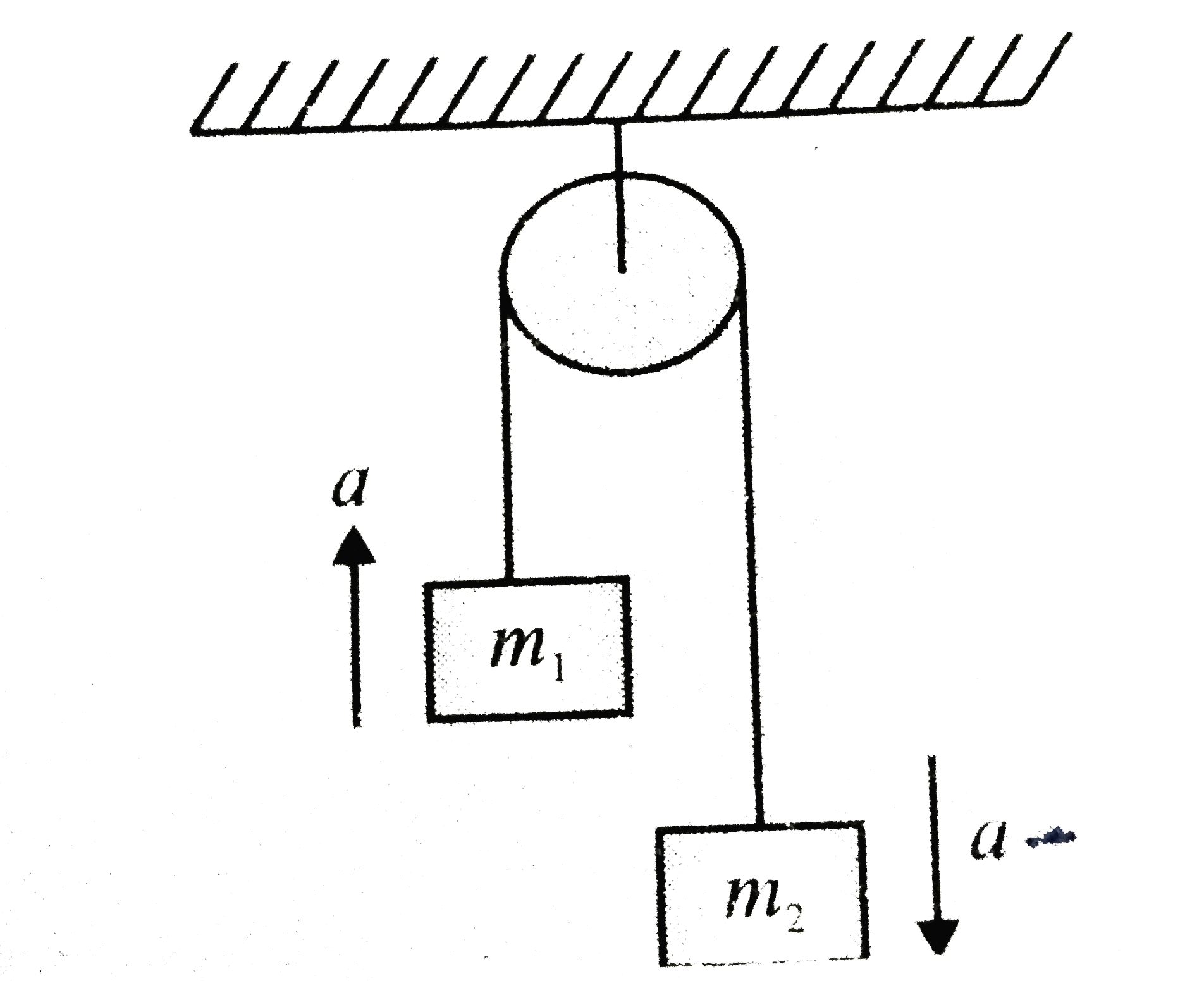
View Solution
Knowledge Check
Two blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
Ag, vertically downwardsBg5, vertically downwardsCg25, vertically downwardsDzeroTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
A7g8,g8B21g8,g8C21g8,g5D12g5,g5A thin uniformed rod of mass m and length L is hinged at one end and from other end a light string is attached. The string is wound over a frictionless pullely (having mass 2m) and a block of mass 2m is connected to string on other side of pulley as shown. the system is released from rest when the rod id making an angle of 37∘ with horizontal. Based on above information answer the following question :
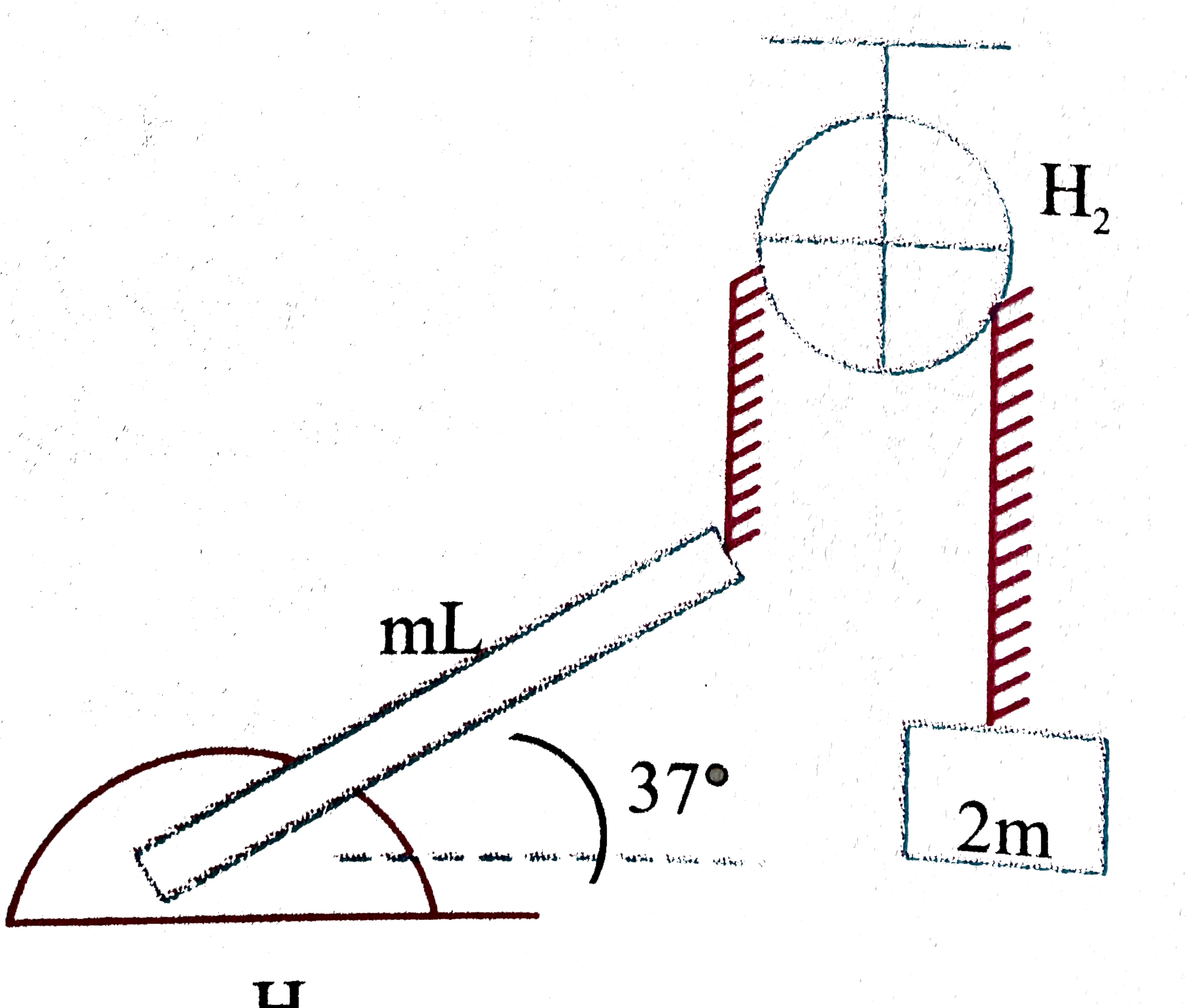
Just after releases of the system from rest acceleration of block isA72g121, downwardsB48g119, downwardsC90g121, downwardsD90g121,upwards
A pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the loads of masses 3m and m . The car starts gong up with acceleration g/s. Assuming the masses of the pulley and the thread, as well as friction, to be negligible, find the force exerted by the pulley on the ceiling of car.

View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
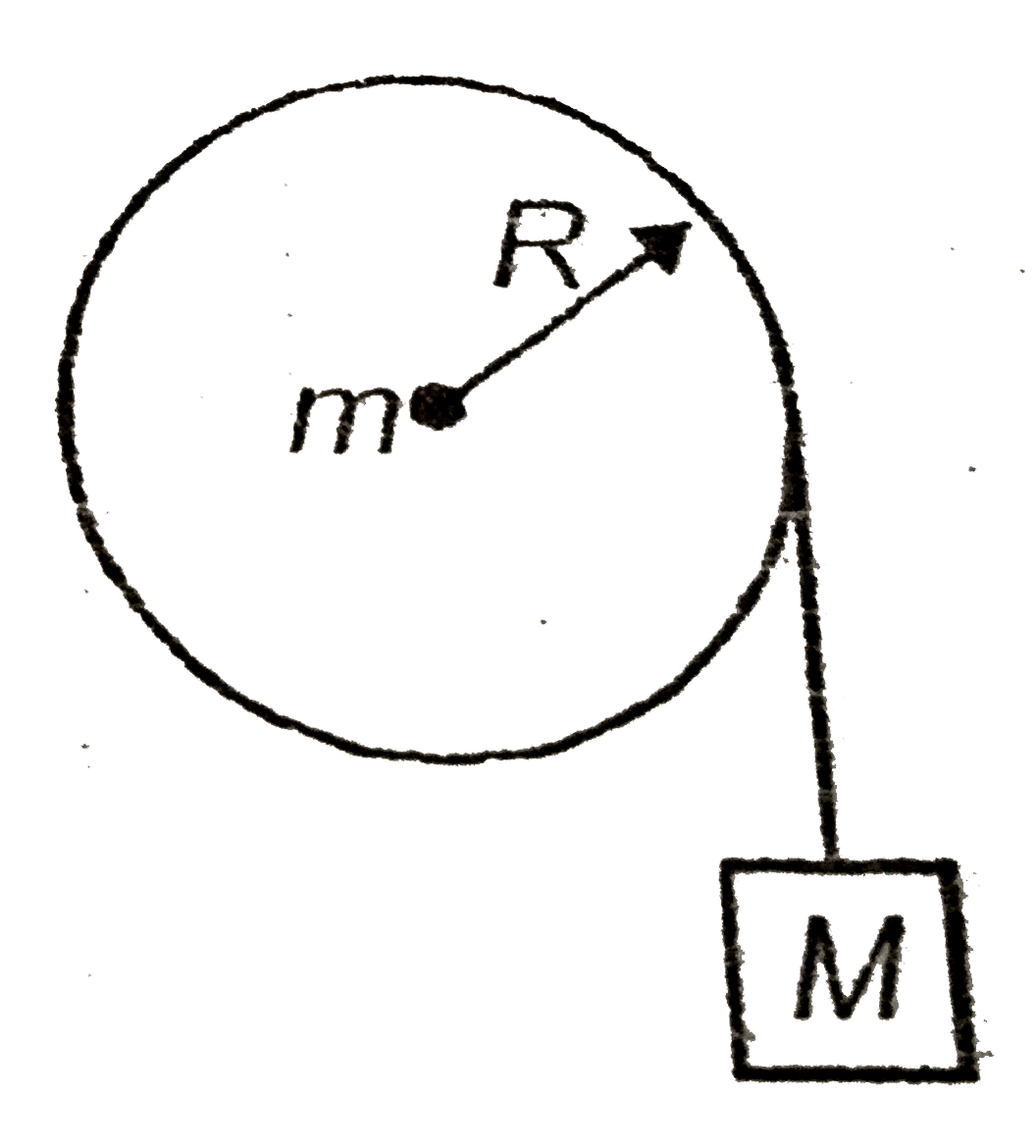
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View Solution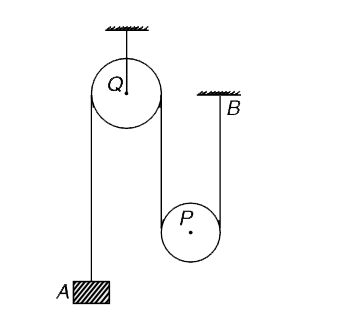
A light thread is wrapped tightly a few turns around a disc P of mass M. One end of the thread is fixed to the ceiling at B. The other end of the thread is passed over a mass less pulley (Q) and carries a block of mass M. All segment of the thread (apart from that on the pulley and disc) are vertical when the system is released. Find the acceleration of block A. On which object – the block A or the ceiling at B – does the thread exert more force ?
View SolutionIn Fig. 6-29, a 2.0 kg block is placed on top of a 3.0 kg block, which lies on a frictionless surface. The coefficient of kinetic friction between the two blocks is 0.30, they are connected via a pulley and a string. A hanging block of mass 10 kg is connected to the 3.0 kg block via another pulley and string. Both strings have negligible mass and both pulleys are frictionless and have negligible mass. When the assembly is released, what are (a) the acceleration magnitude of the blocks, (b) the tension in string 1, and (c) the tension in string 2?

View Solution

