A pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
We know that acceleration of centre of mass of the system is given by the expression.
→wC=m1→w1+m2→m2m1+m2
Since →w1=−→w2
→wC=(m1−m2)→w1m1+m2 (1)
Now from Newton's second law →F=m→w, for the bodies m1 and m2 respectively.
→T+m1→g=m1→w1 (2)
and →T+m2→g=m2→w2=−m2→w1 (3)
Solving (2) and (3)
→w1=(m1−m2)→gm1+m2 (4)
Thus from (1), (2) and (4),
→wc=(m1−m2)2→g(m1+m2)2

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
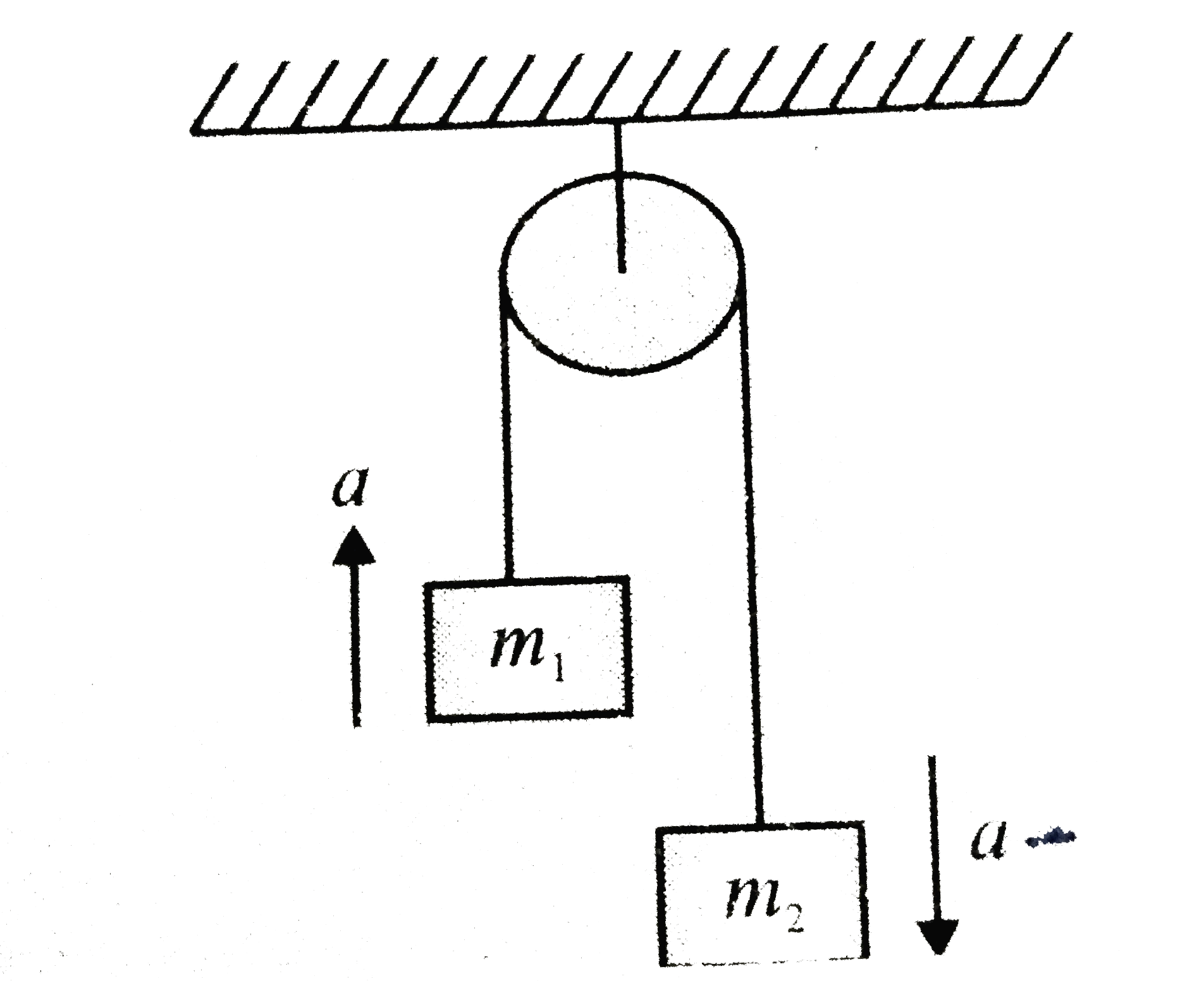
View Solution
Knowledge Check
A pulley fixed to the ceiling carries a string with blocks of mass m and 3m attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
A0Bg/4Cg/2D−g/2Two bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
A(a) (m1−m2m1+m2)gB(b) (m1−m2m1+m2)2gC(c) m1gm1+m2D(d) m2gm1+m2Two blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
Ag, vertically downwardsBg5, vertically downwardsCg25, vertically downwardsDzero
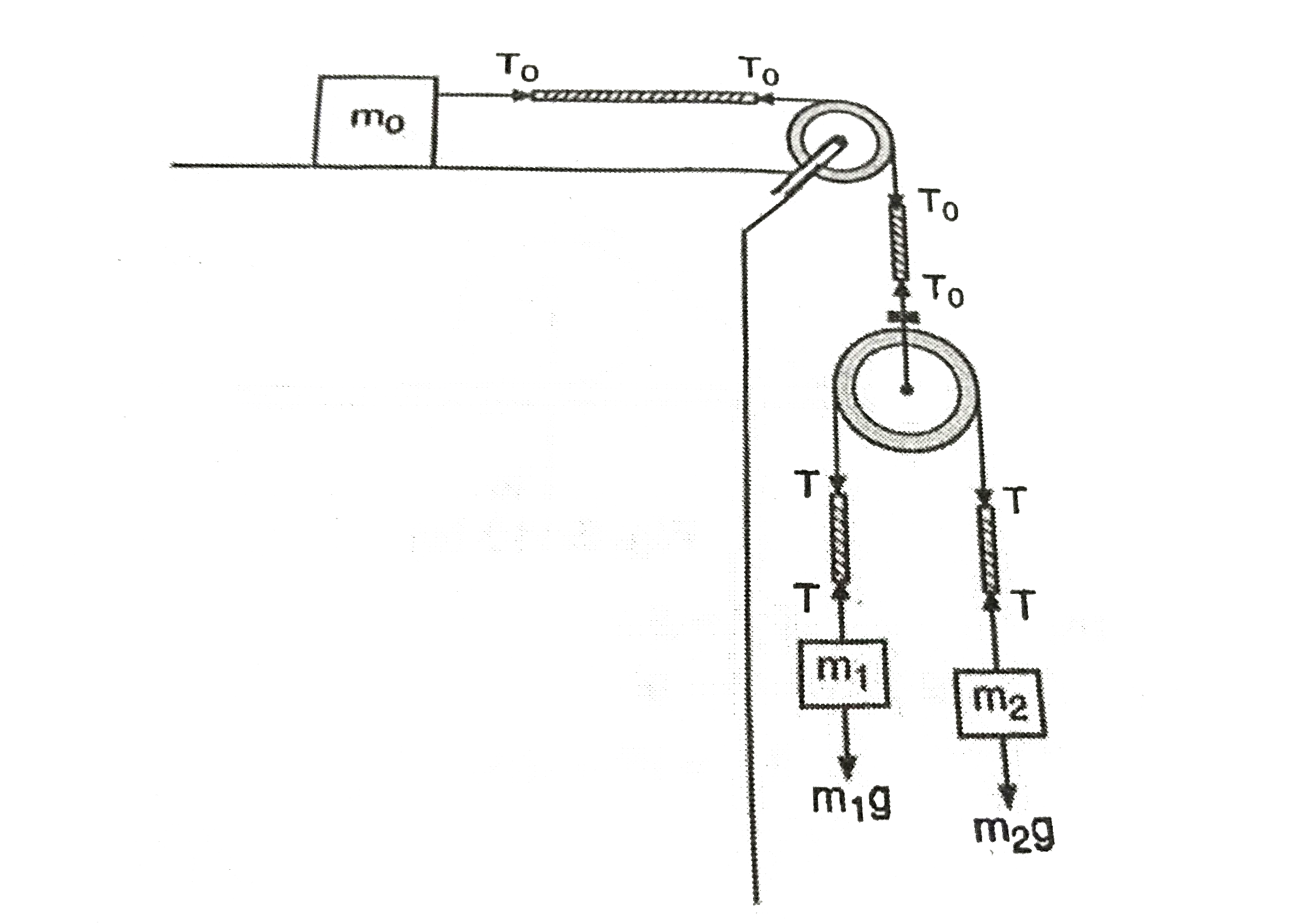
In the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1
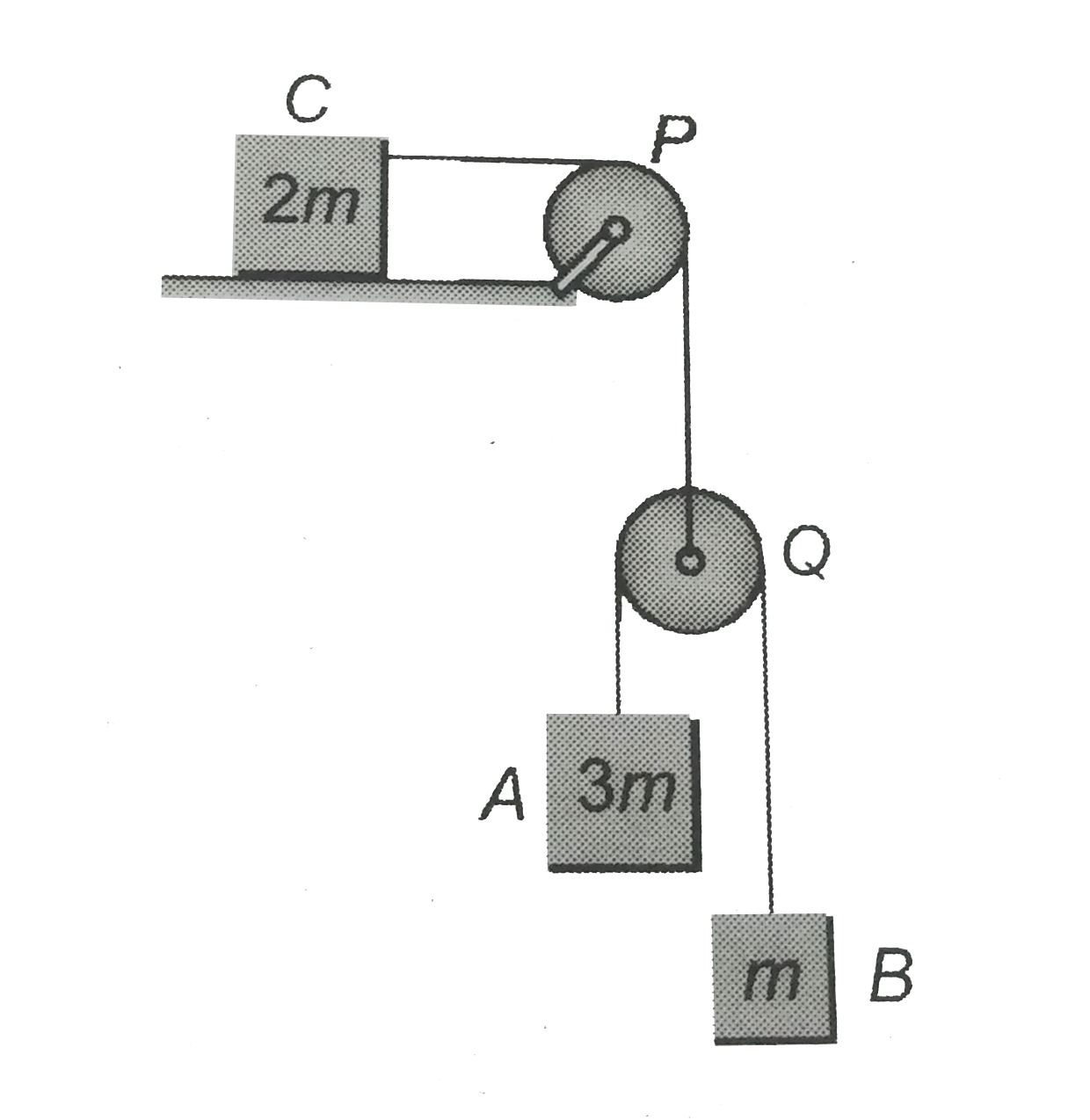
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View SolutionIn the arrangement shown in figure the bodies have masses m0, m1, m2, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of the body m1. Look into possible cases.

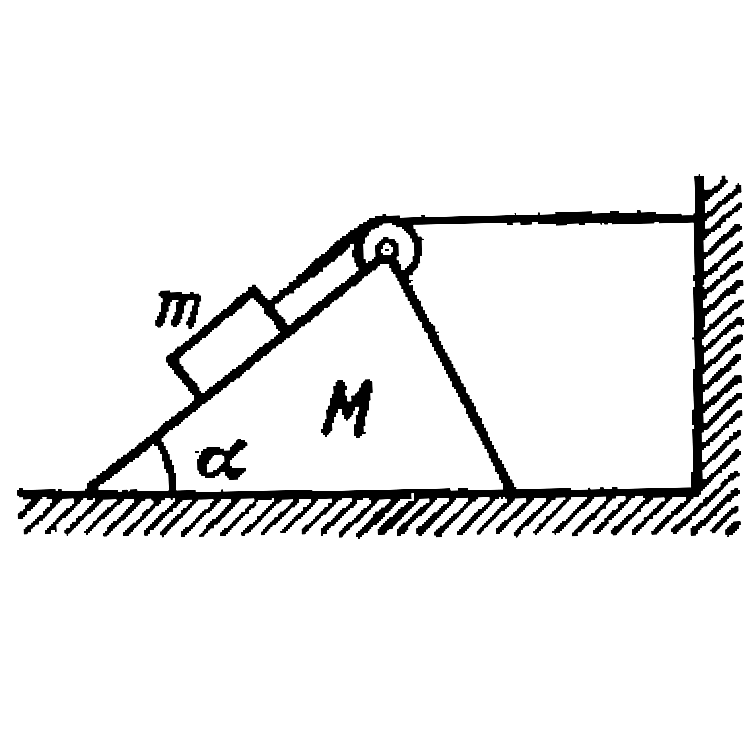
View SolutionIn the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
View SolutionIn the arrangement of figure the masses m0, m1, and m2 of bodies are equal, the masses of the pulley and the threads are negligible, and there is no friction in the pulley. Find the acceleration w with which the body m0 comes down, and the tension of the thread binding together the bodies m1 and m2, if the coefficient of friction between these bodies and the horizontal surface is equal to k. Consider possible cases.

View Solution

