Two bars of masses m1 and m2 connected by a weightless spring of stiffness ϰ (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
After releasing the bar 2 acquires the velocity v2, obtained by the energy, conservation:
12m2v22=12kx2 or, v2=x√km2 (1)
Thus the sought velocity of C.M.
vcm=0+m2x√km2m1+m2=x√m2k(m1+m2)
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Two blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionTwo cubes of mass m1 and m2 are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.

View Solution
Knowledge Check
Two bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
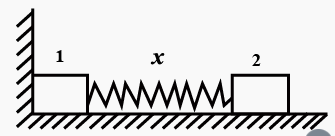 A(a) x0√km2m1+m2B(b) x0m1+m2√km2C(c) x0km1+m2m2D(d) x0√km1(m1+m2)
A(a) x0√km2m1+m2B(b) x0m1+m2√km2C(c) x0km1+m2m2D(d) x0√km1(m1+m2)Two objects of masses 1kg and 2kg separated by a distance of 1.2m are rotating about their centre of mass. Find the moment of inertia of the system
A0.96kgm2B0.48kgm2C0.83kgm2D0.72kgm2Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correct
Two blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
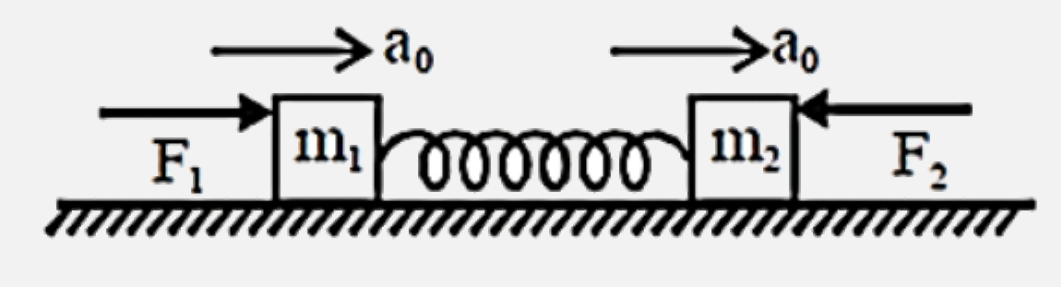
View SolutionTwo cubes with masses m1 and m2 were interconnected by a weightless spring of stiffness x and placed on a smooth horizontal surface. Then the cubes were drawn closer to each other and released simultaneously. Find the natural oscillation frequency of the system.
View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
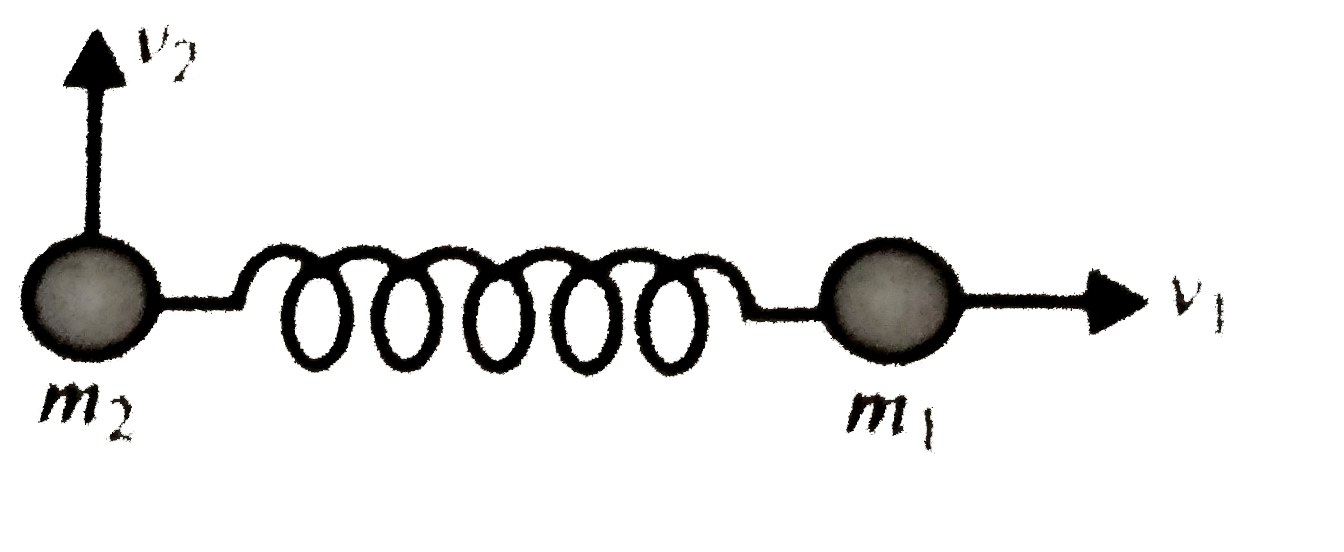
View SolutionTwo small discs of masses m1 and m2 interconnected by a weightless spring rest on a smooth horizontal plane. The discs are set in motion with initial velocities v1 and v2 whose directions are mutually perpendicular and lie in a horizontal plane. Find the total energy ˜E of this system in the frame of the centre of inertia.
View SolutionTwo small discs of masses m1 and m2 are connected by a weightless spring resting on a smooth horizontal plance. The discs are set in motion with initial velocities v1andv2 whose directions are mutually perpendicular and in the same horizontal plane. Find the total energy E of hte system with reference to the frame fixed to the centre of mass.
View Solution

