Find the increment of the kinetic energy of the closed system comprising two spheres of masses m1 and m2 due to their perfectly inelastic collision, if the initial velocities of the sphere were equal to v1 and v2.
For perfectly inelastic collision, in the C.M. frame, final kinetic energy of the colliding system (both spheres) becomes zero. Hence initial kinetic energy of the system in C.M. frame completely turns into the internal energy (Q) of the formed body. Hence
Q=˜Ti=12μ|→v1−→v2|2
Now from energy conservation ΔT=−Q=−12μ|→v1−→v2|2,
In lab frame the same result is obtaiend as
ΔT=12(m1→v1+m2→v2)2m1+m2−12m1|→v1|2+m2|→v2|2
=−12μ|→v1−→v2|2
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Two particles of mass 2m and m moving with speed v and 2v respectively perpendicular to each other collides perfectly inelastically, then
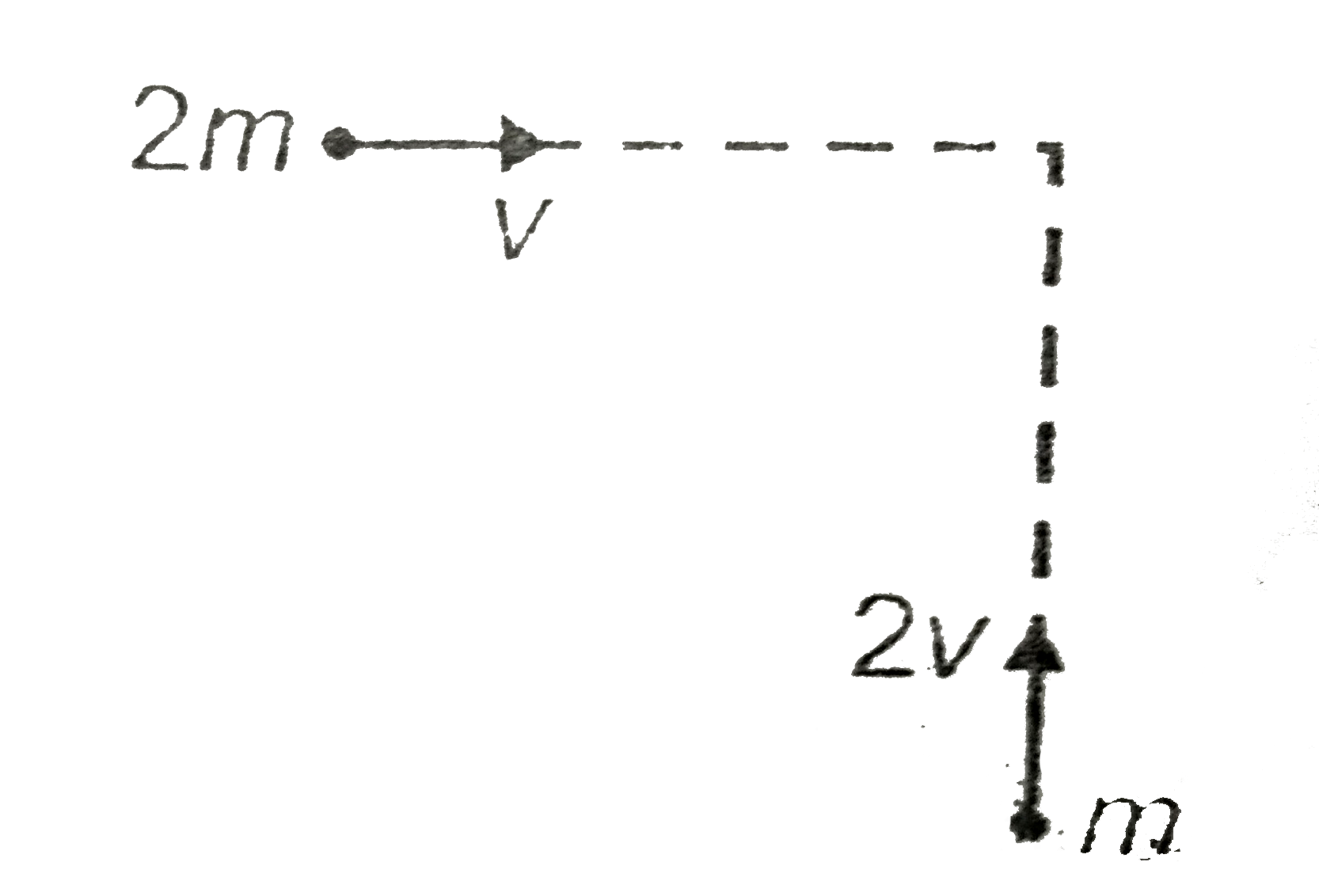
Loss in kinetic energy of the system
View SolutionA sphere of mass m1 moving with a velocity vo hits a sphere of mass m2 that is at rest. The collision is absolutely elastic "and central. The velocities of the spheres after collision are u1andu2, respectively. What are the mass ratios for the following values of velocities: u1=0,u1<0,andu1>0?
View Solution
Knowledge Check
Two particles of mass m and 2 m moving in opposite directions collide elastically with velocities v and 2v. Find their velocities after collision.
A0, 3vB1, 3vC0, 1vD0, 4vTwo identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
AM2(u2−u1)2BM2(u21−u22)CM4(u2−u1)2DM4(u21−u22)Statement-1 : In a perfectly inelastic collision between two spheres, velocity of both spheres just after the collision are not always equal.
Statement-2 : For two spheres undergoing collision, component of velocities of both spheres along line of impact just after the collision will be equal if the collision is perfectly inelastic. The component of velocity of each sphere perpendicular to line of impact remains unchanged due to the impact.AStatement-1 is True, Statement-2 is True,
Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True,
Statement-2 is NOT a correct explanation for Statement-2CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is False
A particle of mass M at rest decays into two particles of masses m1andm2 having velocities V1andV2 respectively. Find the ratio of de- Broglie wavelengths of the two particles
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionThe ratio of kinetic energies of two spheres rolling with equal centre of mass velocities is 2 : 1. If their radii are in the ratio 2 : 1, then the ratio of their masses will be
View SolutionIn perfectly elastic collision between two masses m1andm2 in one dimension energy transfer is a maximum, when
View SolutionA sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
View Solution

