A thin uniform rod AB of mass moves translationally with acceleration due to two antiparallel forces and (figure). The distance between the points at which these forces are applied is equal to . Besides, it is known that . Find the length of the rod.
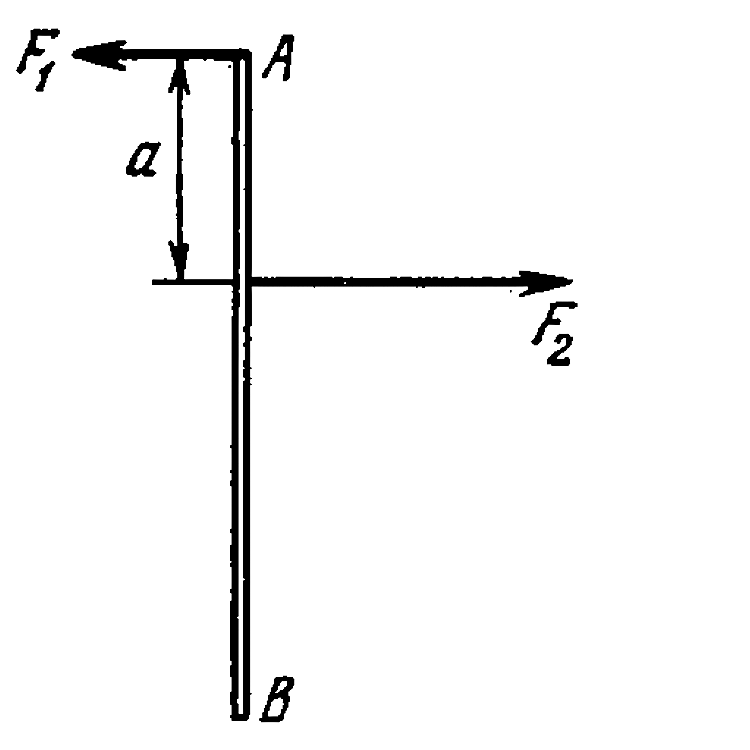
Since, motion of the rod is purely translational, net torque about the C.M. of the rod should be equal to zero.
Thus or, (1)
For the translational motion of rod.
or (2)
From (1) and (2)
or,
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A Thin uniform rod AB of mass m=1.0kg moves translationally with acceleration a=2.0m/s2 due to two antiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to d=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.

View Solution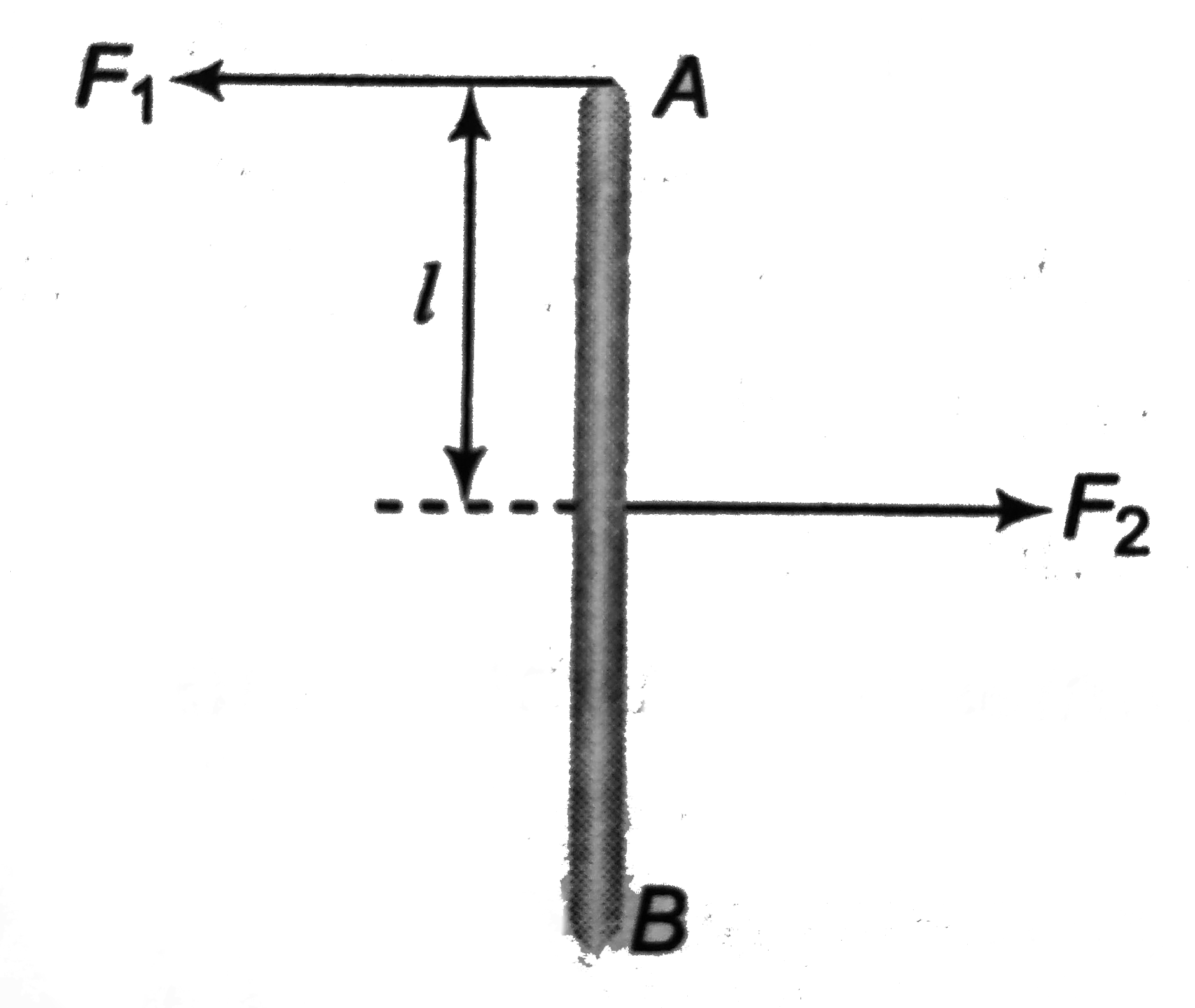
A thin uniform rod AB of mass m=1kg moves translationally with acceleration a=2m/s2 and to two anitiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to l=20cm besides it is known that F2=5N find the length of the rod.
View Solution
Knowledge Check
A thin uniform rod AB of mass 1kg move translationally with acceleration a=2m/s2 due to two antiparallel force as shown. If l=20cm then:
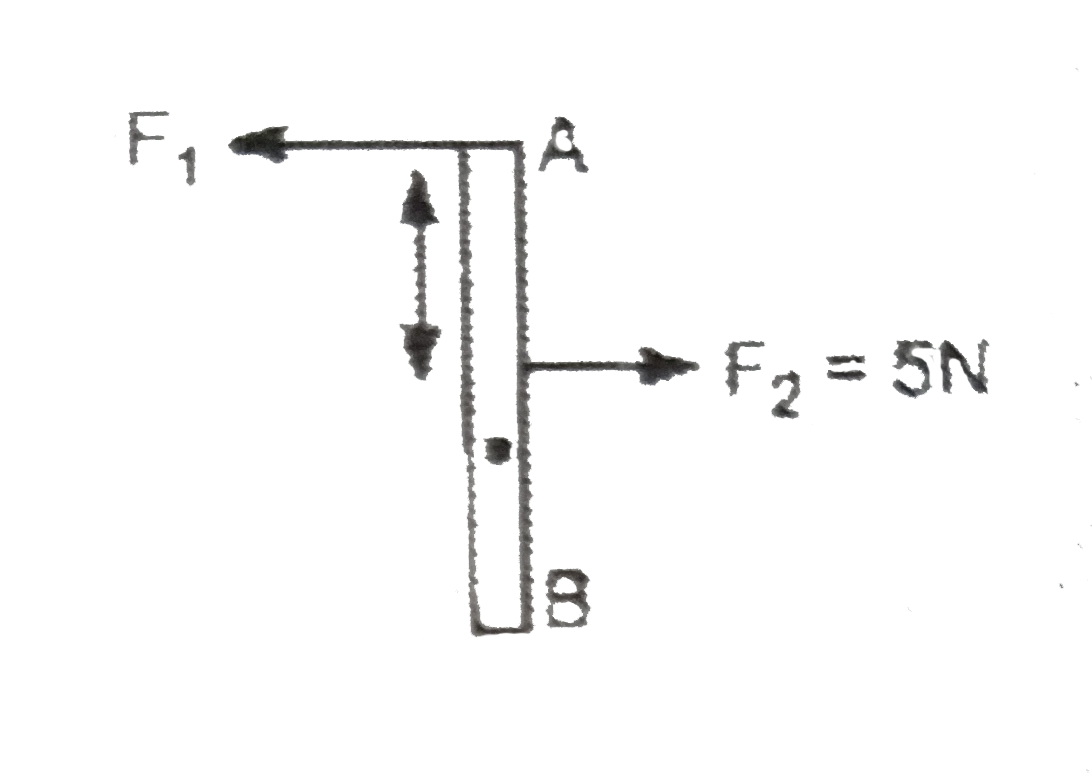 AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cm
AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cmA thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
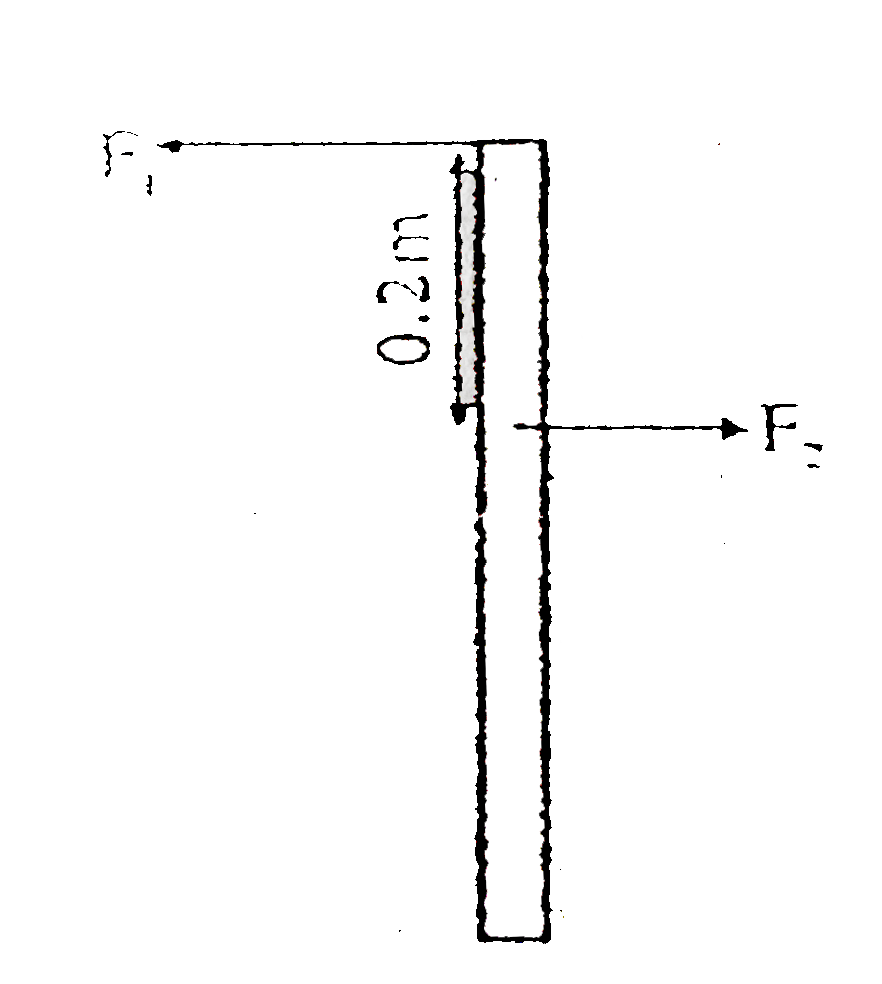 A1 mB2 mC3 mD4 m
A1 mB2 mC3 mD4 mA thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of level arm I. One force is of magnitude F and acts at one extreme end. The length of the rod is
Amalma+FB2(F+ma)lmaCl(l+Fma)D(F+ma)l2ma
In the given figure, thin uniform rod AB of mass kg moves translationally with acceleration a=2ms^(2)due→twoantiparal≤lforcesF_(1) ,F_(2).Thedistancebetweenthep∮satwhichtheseforcesareappliedisequal→0.2 m.IfforceF_(1)=8 N, then find the length of the rod in meter.
'(##CEN_KSR_PHY_JEE_C09_E01_022_Q11##)'
View SolutionA thin uniform rod of mass m=1kg moves translationally with acceleration a=2 ms−1 due to two antiparallel forces of arm-length l=20 cm . One forces is of magnitude 5 N and acts at one extreme end. Find the length of the rod.

View SolutionFind the position of the centre of two unequal antiparallel forces. The distance between the points of application of the forces F1 and F2 is a.
View SolutionA thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
View SolutionA ball of mass 150 g moving with an acceleration 20 m/s2 is hit by a force, which acts on it for 0.1 s. The impulsive force is
View Solution
