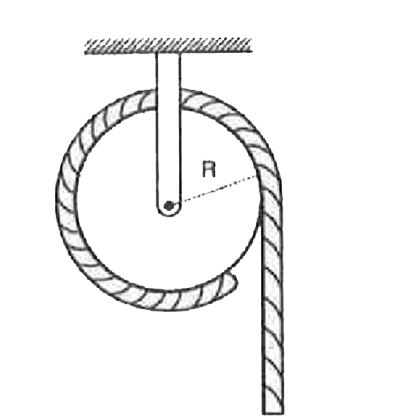
A uniform cylinder of radius $r$ and mass $m$ can rotate freely about a fixed horizontal axis. A thin cord of length l and mass $m_{0}$ is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length $x$ of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.

Video Solution

Text Solution

Verified by Experts

Let us use the equation $\frac{d M_{z}}{d t} = N_{z}$ relative to the axis through O (1)
For this purpose, let us find the angular momentum of the system $M_{z}$ about the given rotation axis and the corresponding torque $N_{x}$ . The angular momentum is
$M_{z} = I ω + m v R = (\frac{m_{0}}{2} + m) R^{2} ω$
[where $I = \frac{m_{0}}{2} R^{2}$ and $v = ω R$ (no cord slipping)]
So, $\frac{d M_{z}}{d t} = (\frac{M R^{2}}{2} + m R^{2}) β_{z}$ (2)
The downward pull of gravity on the overhanging part is the only external force, which exertes a torque about the z-axis, passing through O and is given by,
$N_{z} = (\frac{m}{l}) x g R$
Hence from the equation $\frac{d M_{z}}{d t} = N_{z}$
$(\frac{M R^{2}}{2} + m R^{2}) β_{z} = \frac{m}{l} x g R$
Thus, $β_{z} = \frac{2 m g x}{l R (M + 2 m)} > 0$
Note: We may solve this problem using conservation of mechanical energy of the system (cylinder + thread) in the uniform field of gravity.

Updated on:21/07/2023

A uniform solid cylinder of mass $m$ and radius $R$ is placed on a rough horizontal surface. A horizontal constant force $F$ is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
A $F / 3 m$
B $2 F / 3 m$
C $4 F / 3 m$
D $5 F / 3 m$
A homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
A $\frac{2 F}{3 M r}$
B $\frac{3 F}{2 M r}$
C $\frac{F}{3 M r}$
D $\frac{F}{2 M r}$
A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
A $M R F$
B $\frac{M R}{F}$
C $\frac{R}{M F}$
D $\frac{F}{M R}$