A uniform cylinder of radius R, and mass M rotates freely about a stationary horizontal axix O. A thin cord of length l and mass m is wound on the cylinder in a single layer and its free end is falling vertically. Find the acceleration as a function of the length x of the hanging part of the cord. Assume the center of mass of the wound part of the cord to be the axis of the cylinder. 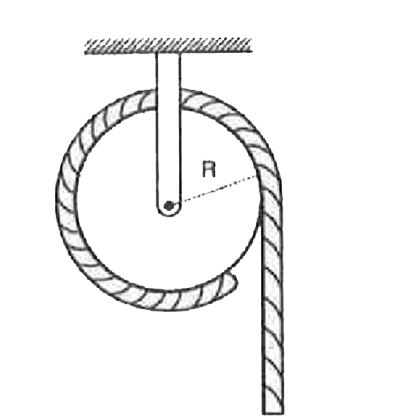
The correct Answer is:α=2mgxl(M+2m)R
Step by step video, text & image solution for A uniform cylinder of radius R, and mass M rotates freely about a stationary horizontal axix O. A thin cord of length l and mass m is wound on the cylinder in a single layer and its free end is falling vertically. Find the acceleration as a function of the length x of the hanging part of the cord. Assume the center of mass of the wound part of the cord to be the axis of the cylinder. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABook:NN GHOSHChapter:ROTATIONAL DYNAMICS, MOMENT OF INERTIAExercise:Exercises
Explore 42 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBook:NN GHOSHChapter:MOMENT, TORQUE, EQUILIBRIUM OF BODIESExercise:Exercises
Explore 33 Videos
- SATURATED AND UNSATURATED VAPOURBook:NN GHOSHChapter:SATURATED AND UNSATURATED VAPOURExercise:All Questions
Explore 1 Video
Similar Questions
A uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin cord of length l and mass m0 is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length x of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.

View SolutionThread would around cylinder of mass M and radius R. It is allowed to fall as shown. Find its acceleration.

View Solution
Knowledge Check
A uniform cylinder of mass m rests on two rough horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F
ASince horizontal acceleration is provided by the friction acting on the cylinder, its translation kinetic energy (12mv2) is equal to work done by this friction,BSince moment about instantaneous axis of rotation is produced by force F. kinetic energy (12Iω2) is equal to work done by F where I is moment of inertia about the instantaneous axis of rotation and ω is the-angular velocity.CSince cylinder is moving, energy is lost against friction.DWork done by F+ work done by friction on cylinder =totalKE of the cylinder.A uniform chain of length L and mass M is tying on a smoth table and one third of its length is banging vertically down table the edge of the table if g is acceleration the to gravity , the work required to pull the hanging part on the table is
AMgLBMgL/3CMgL//9DMgL//18A cylinder of mass 50mg and radius 0.5m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 revolutions s−2 is
A25 NB50 NC78.5 ND157 N
What is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
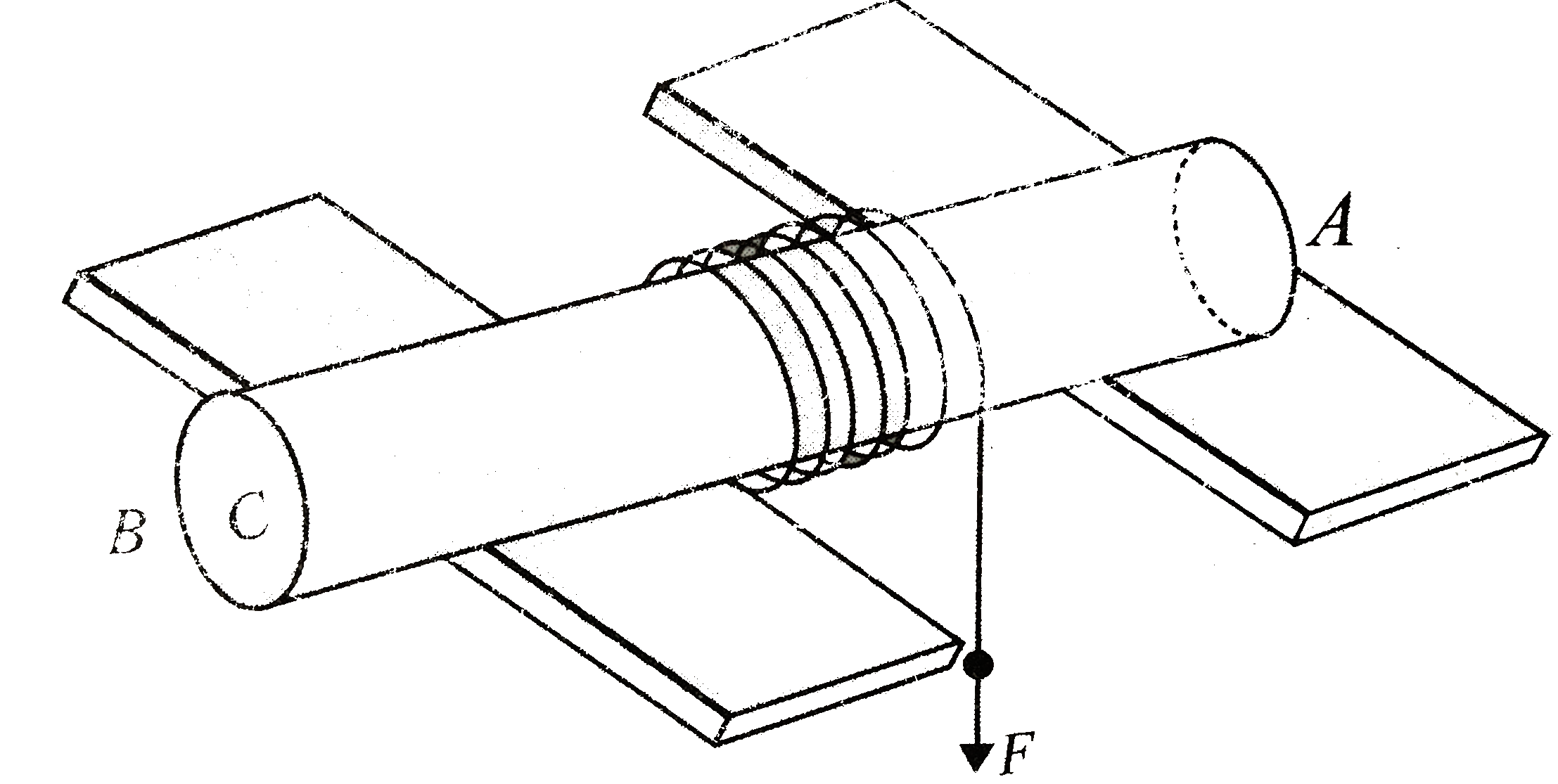
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionFind radius of gyration of a rod of length l and mass m about an axis perpendicular its length through one end.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution

