A uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a mount B of mass m2(figure). A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find:
(a) the acceleration of the point K,
(b) the kinetic energy of this system t seconds after the beginning of motion.

(a) For the transational motion of the system (m1+m2), from the equation : Fx=mwcx
F=(m1+m2)wc or, wc=F/(m1+m2) (1)
Now for the rotational motion of cylinder from the equation: Ncx=Icβz
Fr=m1r2rβ or βr=2Fm1 (2)
But wK=wc+βr, So
wK=Fm1+m2+2Fm1=F(3m1+2m2)m1(m1+m2) (3)
(b) From the equation of increment of mechanical energy :ΔT=Aext
Here ΔT=T(t), so, T(t)=Aext
As force F is constant and is directed along x-axis the sought work done.
Aext=Fx
(where x is the displacement of the point of application of the force F during time ineterval t)
=F(12wKt2)=F2t2(3m1+2m2)2m1(m1+m2)=T(t)
(using Eq. (3)
Alternate: T(t)=Ttranslation(t)+Trotation(t)
=12(m1+m2)(Ft(m1+m2))2+12m1r22(2Ftm1r)2=F2t2(3m1+2m2)2m1(m1+m2)

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Hydrodynamics
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
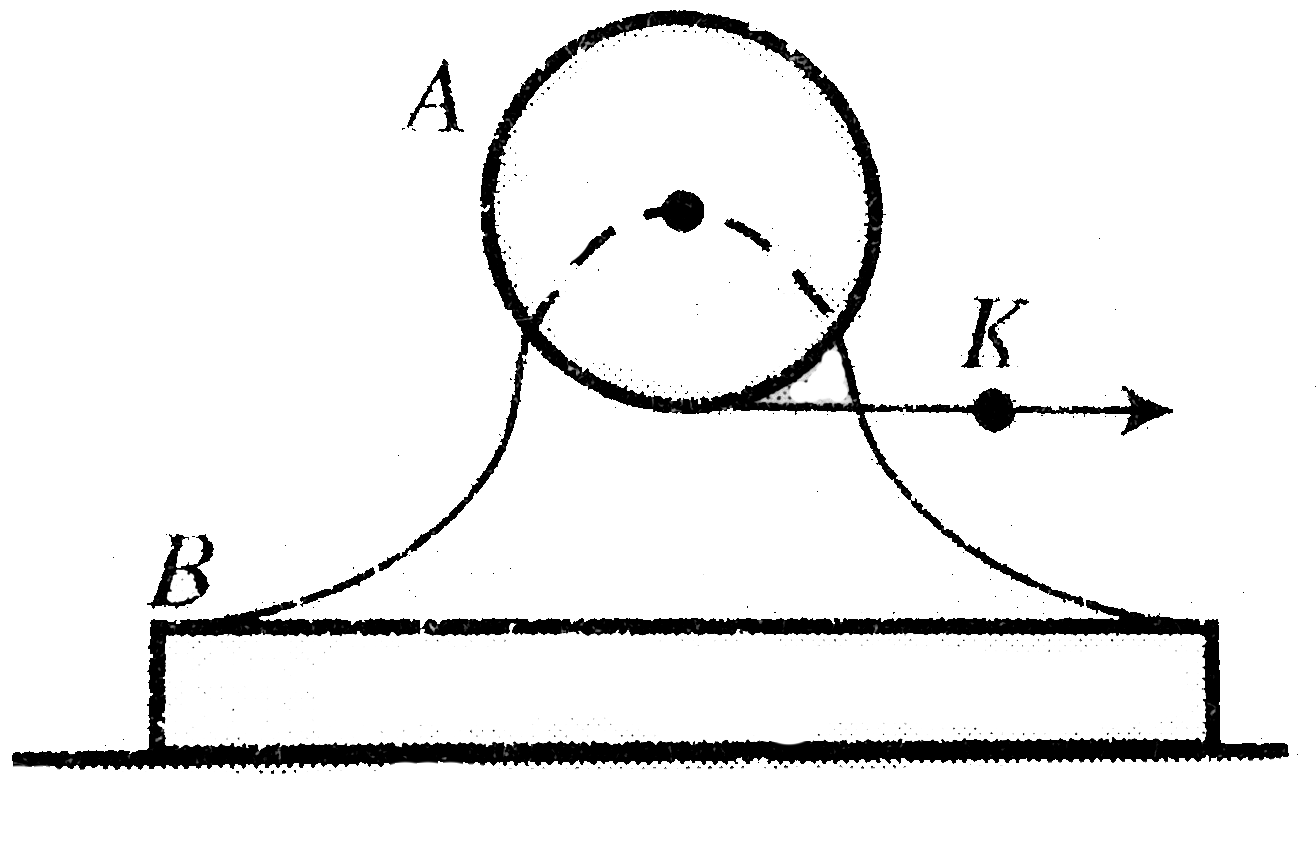
View SolutionA uniform solid cylindrical roller of mass m and R is rolled on the ground , without slipping , by applying a constant horizontal force F. Find angular acceleration of cylinder .

View Solution
Knowledge Check

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3mA horizontal force F is applied on a riing of mass m1 constrained to move on a horizontal smooth wire the hanging mass m2 is constant angle with
 AForce on m1 by wire is less than (m1+m2)gBNet force on m2 is m2Fm1+m2CTension in rod is m2gsecθDF=(m1+m2)gtanθ
AForce on m1 by wire is less than (m1+m2)gBNet force on m2 is m2Fm1+m2CTension in rod is m2gsecθDF=(m1+m2)gtanθ
On an uniform cylinder of mass m and radius R a constant horizontal force F is applied at any point. Choose the correct alternative if cylinder is rolling without slipping in rightward direction

View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
View SolutionA uniform cylindrical pulley of mass M and the radius R can freely rotate about the horizontal axis O (figure). The free end of a thread tightly wound on the pulley carries a deadweight A. At a certain angle α it counterbalanes a point mass m fixed at the rim of the pulley. Find the frequency of small osicllations of the arrangement.
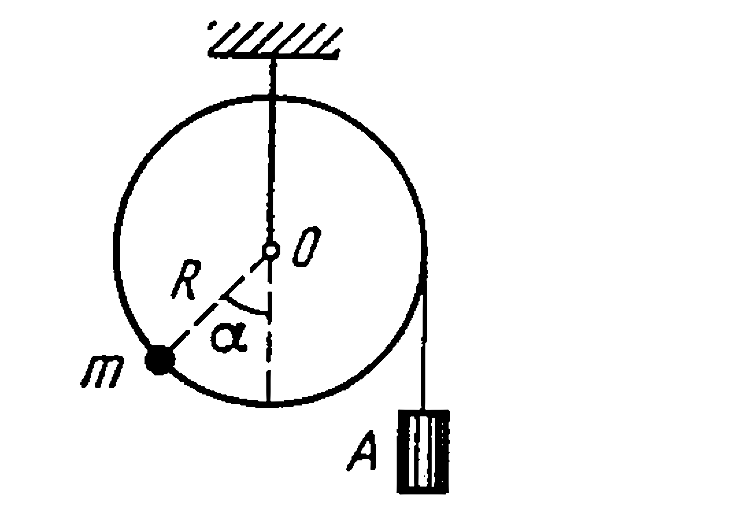
View SolutionA plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA lawn roller in the form of a thin-walled hollow cylinder of mass M is pulled horizotally with a constant horizontally force F applied by a handle attached to the axle. If it rolls without slipping. Find the acceleration and the friction forces.
View Solution