A horizontally oriented uniform disc of mass $M$ and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass $m$ . A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with and angular velocity $ω_{0}$ . Then by means of a force $F$ applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.

Video Solution

Text Solution

Verified by Experts

(a) As force F on the body is radial so its angular momentum about the axis becomes zero and the angular momentum of the system about the given axis is conserved. Thus
$\frac{M R^{2}}{2} ω_{0} + m ω_{0} R^{2} = \frac{M R^{2}}{2} ω$ or $ω = ω_{0} (1 + \frac{2 m}{M})$
(b) From the equation of the increment of the mechanical energy of the system:
$Δ T = A_{e x t}$
$\frac{1}{2} \frac{M R^{2}}{2} ω^{2} - \frac{1}{2} (\frac{M R^{2}}{2} + m R^{2}) ω_{0}^{2} = A_{e x t}$
Putting the value of $ω$ from part (a) and solving we get
$A_{e x t} = \frac{m ω_{0}^{2} R^{2}}{2} (1 + \frac{2 m}{M})$

Updated on:21/07/2023

A uniform disc of mass $M$ and radius $R$ is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.

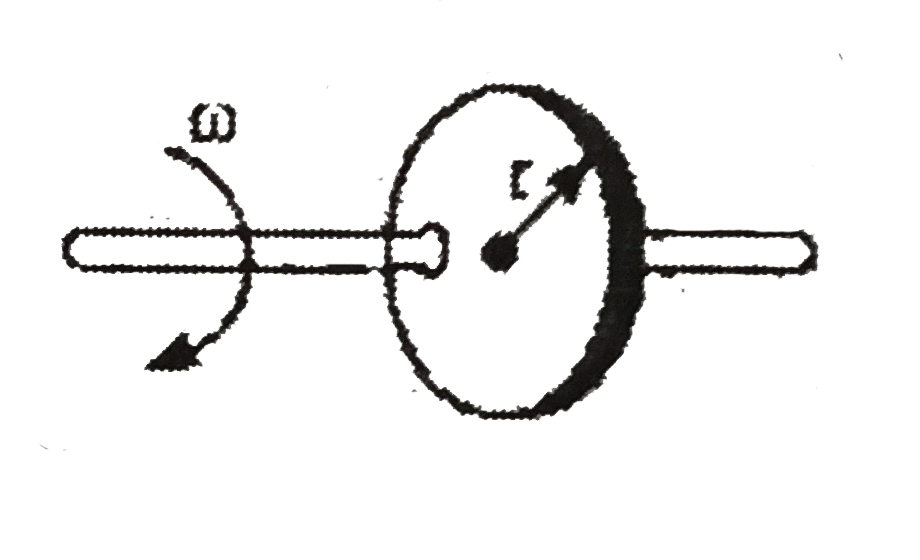AThe angular velocity of disc when its centre of mass is directly below the pivot is $\sqrt{\frac{4 g}{3 r}}$
BThe force exerted by the pivot at this instant is $\frac{7}{3} m g$
CAngular momentum of disc is conserved
DAngular acceleration of disc at the given instant is zero
The M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
A $\frac{1}{2} M R^{2}$
B $\frac{1}{4} M R^{2}$
C $M R^{2}$
D $\frac{3}{4} M R^{2}$
A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity $ω$ . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A $\frac{(M - 2 m) ω}{(M - m)}$
B $\frac{(M + 2 m) ω}{(M + m)}$
C $\frac{(M - 2 m) ω}{(M + m)}$
D $\frac{(M + 2 m) ω}{(M - m)}$